初中数学认知冲突教学策略的设计

陈平

摘要]认知冲突是课堂有效教学的拐点，也是衡量教师教学技能的标点. 认知冲突教学策略的设计，主要有以下多种策略：在教学情境中引发认知冲突;在知识矛盾中引发认知冲突;在困惑中引发认知冲突;在讨论中引发认知冲突;从“尝误”中引发认知冲突;从发散思维中引发认知冲突.

[关键词]初中数学认知冲突课堂教学设计

[中图分类号]G633.6[文献标识码]A[文章编号]16746058（2015）140009

认知冲突是学生原先建立的知识体系或认知结构与呈现在眼前的学习情境不相吻合而引发的矛盾与冲突.在数学课堂教学中，教师要利用好学生的认知冲突，激活学生的学习思维，促使学生积极参与学习活动.因此，在课堂教学中设置认知冲突，关注知识结构上的联系点、衔接点和转折点，关注学生认知结构上的新起点、新坡度和新频率，有效开展课堂教学，一方面可以激发学生的学习兴趣，活跃课堂气氛，另一方面也能锻炼学生的思维.有效教学必须引发学生的认知冲突，有效的认知冲突不仅是动感课堂的重要标志，更是学生数学思维深度发展的重要平台.本文试图从八个方面谈谈认知冲突教学策略的设计.

一、从学生的生活实际出发，在新情境中引发认知冲突

《数学课程标准》中指出：“要重视从学生的生活经验和已有知识中学习数学和理解数学;要让学生学有用的数学，通过解决实际问题，使学生在掌握数学内容的同时，形成对自己素质发展有促进作用的基本数学思想方法.”因此在教学中，教师必须根据学生的实际情况，利用学生的生活经验，创造一种认知上的冲突环境，激发学生强烈的学习兴趣和探究欲望.因而，教师可以提出一些贴近学生生活的问题，也可以创设一个使学生感兴趣的问题情境，引发学生用已学知识无法解决的冲突，激发学生学习新知的欲望.

比如，在教学“数据的代表”中“中位数与众数”时，可创设情境如下.

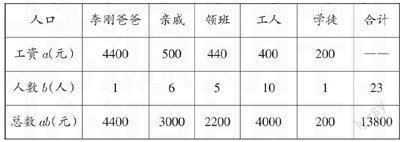
李刚同学的爸爸有一个小工厂，管理人员有李刚的爸爸，另外还有6个亲戚;具体的操作人员中有5个领班、10个工人和1名学徒.现在需要增加一个新工人.

小孙去应聘时，与李刚的爸爸进行了交谈.李刚的爸爸说：“我们这里的报酬应该说还是不错的，平均工资是每周600元.”小孙去工作几天后，找到李刚的爸爸说：“你欺骗了我，我已经问过其他工人了，没有一个工人的工资超过每周400元，平均工资怎么可能是一周600元呢？”李刚的爸爸说：“小孙，平均工资是600元，你可以看看这张工资表.”

问题：①李刚爸爸说每周平均工资600元是否欺骗了小张？②平均工资600元能否客观地反映工人的平均收入？

上述问题一呈现，学生异常兴奋，思维活跃.通过对此问题的讨论、分析、解答，学生切身体会到数学就在身边，真实感受到了学数学、用数学的乐趣.实践表明，在课堂教学中创设这样的生活问题情境，能使学生从内心接受数学，喜欢数学，进而产生浓厚的学习兴趣，为创新意识的培养提供有利条件.从认知角度而言，教学需要创设一个真实的问题情境，这是因为疑问是学生学习的起点，它可以提示学生认知上的矛盾，可以对学生的心理产生刺激，有利于帮助学生建立新的认知结构.

二、从学生的已学知识出发，在新旧知识矛盾中引发认知冲突

学生的已有知识和生活经验是学生学习新知识的基础.同时，认知心理学家认为，当学习者发现不能用头脑中已有的知识来解释一个新问题或发现新知识与头脑中已有的知识相悖时，就会产生“认知失衡”，这时就需要教师正确的引导，使学生重新寻找到新的“平衡点”.这种“平衡点”的建立过程就是推动学生认知需要（内驱力），萌发学生探索未知领域的强烈愿望的过程.充分利用学生已学知识的局限性，挖掘教材中的矛盾因素和学生的思维误区，利用富有挑战性、探索性且处于学生认知结构的最近发展区的问题素材，把学生置于矛盾中，让他们感到已有知识还不能解决问题，引发认知冲突，从而使学生产生解决矛盾的迫切心理，并进行有效的学习.

比如，在教学七年级第一节课“负数”时，先回顾自然数、分数的由来，再列举生活中与负数有关的几个例子，让学生自己明白小学已学的正数已不足以解决问题.又如，在“实数”教学中，教师先告诉学生：“我们在小学先学了整数，如1、2、3、4、5……，接着我们学了与整数相对的数——分数.到初中我们把整数与分数合并为有理数，那么，与有理数相对的数是什么数？”学生很快就会回答：“无理数.” “如果我们把有理数和无理数合并叫做实数，那么，与实数相对的数又可以叫做什么数呢？”“虚数.”学生答道.“同学们，你知道2是什么数吗？”此时学生在心理上产生求知欲望，激发了学习兴趣.

再如，在八年级的分式复习课中，教师出了这样一道题：在日常生活中，我们知道在一杯糖水中加糖后，糖水会变得更甜，若原有糖水a克，其中含糖b克（a>b>0），后来加入m克糖，则这一现象用数学式子表示为.

师：“甜”的程度可用什么来衡量？

生：质量分数.

师：加糖前的质量分数与加m克糖后的质量分数分别怎么表示？

生：加糖前质量分数为ba，加m克糖后则质量分数为b+ma+m.到这里，问题的答案已非常明显，ba

师：你能否利用分式的性质说明这个式子成立的理由？

在解题过程中，教师抓住“更甜”的关键点，激发学生的学习兴趣，“更甜”就是质量分数更大，无形中强化了学生利用生活经验解决数学问题的思维，使学生感受到数学就在身边，生活中到处有数学.反过来，学好数学可使人们更加合理地做出判断和选择.

没有认知冲突的课堂就像一潭没有涟漪的静水，难以激发学生的学习情感，也难以走进学生的思维天地，教学效果自然不佳.因此，在教学中设置认知冲突，一方面可以激发学生的学习兴趣，活跃课堂气氛，另一方面也能锻炼学生的思维，提高学生分析问题、解决问题的能力.

三、设置知识“跳跃点”，在困惑中引发认知冲突

研究表明，学生在原有的知识上“跳一跳，够得着”而产生的问题，最能引发学生的认知冲突.这里最关键的是教师要比较充分地了解学生对旧知识的掌握程度和教材要求，发掘知识“跳跃点”，才能有针对性地创设冲突情境，使学生处于“心欲求而不得，口欲言而不能的“愤”“悱”状态，激起学生的强烈情感与求知欲.

比如，在教学七年级数学“1.4.1有理数的乘法（一）”时，教师先让学生通过竞赛的形式，计算熟悉的“3×4=;3×3=;3×2=;3×1=;3×0=”算题.这时学生会因感觉到太简单而麻痹大意.教师再给出几个有负因数的题目“4×（-1）=;（-4）×（-2）=”，这时，学生按照定式思维计算得出4、-4、8、-8、-6等多种答案，学生带着认知上的冲突参与学习，激发了学习的热情.

现代教育理论认为，最有效的学习是学生对学习过程的体验，它能给予学生自主构建知识和情感体验的时空，启发学生的思维.教师抓住文章的矛盾处，给学生提供一个语言交流的平台，让学生通过读句子，进入有认知冲突的真实情境中，从而使自己产生疑问，激起认知冲突.这种认知冲突是锻炼学生思维，提高学生认识水平的最佳方式.学生带着这些“困惑”去学习，探究的积极性无疑会更加高涨.

四、设置有争议的实践操作，在讨论中引发认知冲突

实践操作是数学教学中常用的教学方法，能让学生在动手中得到思维的锻炼.但由于学生存在实践操作、知识掌握运用、观察问题角度方面的问题，对于通过实践操作可以完成的问题，却总是得不到应该得到的结论，或不能对一些结论进行验证，找不到解决的方法，与教学预设相差甚远.或者，同样的任务或问题，由于操作的方式方法不同，因而得到的结论也可能出现差异.这种认知冲突，需要教师对学生实践操作的过程给予密切的关注，及时指导学生发现冲突的原因及症结所在，从而有针对性地加以改进.

比如，在教学“立方体表面展开图”时，教师组织学生用剪刀沿着立方体的棱将其剪开铺平，经过动手操作，学生发现剪法不同，立方体的表面展开图也可能不同.教师及时抓住学生在具体实践过程中出现的这种情况，或让学生提出发现的问题，或让小组成员相互观察，帮助学生找寻规律.这个冲突的利用，不仅激发了学生继续探究的欲望，也引出了“分类讨论”的数学思想.

又如，教学八（下） “平行四边形及其性质”这节课时，教师依据教材设计了这样一个实践活动：请用纸剪出两个全等的三角形，将这两个全等三角形进行拼图.①最多能拼出几个平行四边形？②如拼出的平行四边形（能重叠的只算1个）只有一个，那剪出的两个三角形是什么形状？③若只能拼出三个平行四边形，那剪出的两个三角形又是什么形状？

学生一一进行了操作.

就在师生基本上认为已经比较完美地解决了问题时，一学生突然站了起来，说：“老师，两个全等的直角三角形的两条斜边重叠时，有一个图形是一个长方形，不能算是一个平行四边形.”有不少学生纷纷认可这个结论.于是，教师就问他：“长方形为什么不能算是平行四边形？”他说：“长方形的角是直的，而平行四边形的角不是直的.”教师在表扬他能动脑筋思考的同时，让大家回忆一下平行四边形的定义，最后大家都比较满意地得到了结果.

心理学家皮亚杰认为：“思维是从动作开始的，切断了动作和思维之间的联系，思维就得不到发展.”教师要重视实践活动，真正放手让学生操作，让操作成为培养学生创新思维的源泉.同时，人的认知水平是在“已知区”“最近发展区”“未知区”这三个层次之间循环往复，不断变化，螺旋式上升的.正确地认识学生的已有发展水平及其潜在的发展可能，合理地组织引导，使教学建立在学生的潜力发展水平上.教师要从特殊到一般的思路点拨，把学生的思维从模糊引向光明，从而使其形成正确的思路，在认知冲突的多次循环中实现教学的精彩和成功.

五、利用学生新知的偏差，从“尝误”中引发认知冲突

利用数学知识结构中的模糊点、易错点或盲点，设置相应的知识陷阱，引诱学生落入其中，再将学生从中“救起”或引导学生进行“自救”.此举对“纠错”或“究错”十分有效.“尝误”的问题包括思维策略技巧问题、思维角度问题、资料分析处理技巧问题、情感态度倾向问题、理解过程问题、现象观察的认识等.教师要善于发现学生的学习行为表现，及时发现学生的学习困难，引导学生对学习困难进行描述，使之清晰地成为学生的认知冲突.

比如，在教学“5.2.2平行线的判定”时，有这样一道例题：在同一平面内，如果两条直线都垂直于同一条直线，那么这两条直线平行吗？为什么？在证明完毕后，有学生提出：“为什么条件要‘在同一平面内，不要这个条件可以吗？”冲突一提出，学生讨论的热情一下子被激发出来了.

另外，利用隐含条件是引发学生认知冲突的有效策略，会让学生产生“山重水复疑无路”的迷茫，激发学生探究和发现问题的迫切愿望.然后，教师引导学生再次审题，反思解题过程，给学生指点迷津，让学生找到解题的突破口，使学生产生 “柳暗花明又一村”的快感.如在“二次根式”的教学中，教师为了让学生更深入地理解二次根式的性质，可举例：化简x2-4x+4-（2x-3）2.若学生没有发现“2x-3≥0”这一隐含条件，那么就会出错.从“尝误”中爆发认知冲突，能优化学生的解题思路，帮助学生掌握严谨的思维方式，养成良好的审题习惯，进而培养学生敏锐的洞察力.

错误是正确的先导，是成功的开始.学生所犯的错误及其对错误的认识，是学生知识宝库的重要组成部分.他们在发生错误、纠正错误的过程中，获得知识，提高能力，增进对数学知识的情感体验.因而，捕捉学生在学习过程中出现的错误，发现错误背后隐藏的教学价值，是提高教学有效性的主要途径.

六、让学生经历思维挫折，从发散思维中引发认知冲突

“数学是思维的体操.”在数学课堂教学中，教师应注重对学生思维方式的引导，使学生形成多向、灵活、善变的思维，避免学生用一种固定的思维方式去思考问题，鼓励学生拓宽思路，从不同的角度思考问题，寻找解决问题的捷径，这样有利于提高学生的思维水平.

教师可以有意拉大思维的跨度，或提出与常规看法相悖的问题，设计开放性问题和用常规方法无法解决的问题 ，巧妙地设置思维障碍，让学生经历思维上的挫折，引发认知冲突，促使学生把注意力集中到知识的重点和关键点上，积极探索解决问题的方法.比如，在“函数的应用”教学中，教师设计以下问题让学生解答：方程2x-x2=2x的正根有几个？一开始，学生会采用方程思想求解，但由于去分母后得到方程x3-2x2+2=0，对于初中生来说，他们无法求解该方程，在思维上形成障碍，学生的心理产生改变解题策略的欲望.这时，教师启发学生利用函数图像法求近似解，学生便会豁然开朗.

此外，变式训练是培养学生发散性思维的有效方法.在数学习题教学中，不能把思路局限于一个问题或问题的一种状态下，应善于将题目中的已知条件、设问角度、求解的目标或图形作适当改变，加强变式训练，强化认知冲突，激发学生探究问题的兴趣和热情.在几何教学中，经常利用图形的动态变换实施变式训练.通过图形的动态变换，引发图形的形状、数量关系和位置关系的变化，而这种变换往往是从简单到复杂，从特殊到一般的过程.

比如，在教学“三角形中位线”时，教师先让学生借助度量和平行线的判定方法猜想得出三角形中位线定理，然后让学生将三角形沿中位线剪开后拼成一个平行四边形，并合作探究相关证明方法，学生很容易得到如图1的平行四边形和相应的证法.在此基础上，教师让学生继续合作探究：能否将上述两个图形继续分割并“拼图”，得到其他形状的平行四边形或矩形？你能得出新的证明方法吗？学生会得到如图2、图3这两种较特殊的图形和相应的证法.教师追问：如将△ADE从A点沿任意一条直线剪开（如图4）行吗？你还能发现其他方法吗？学生会发现如图5的拼法.

图1图2图3图4图5

学生通过经历上述的操作、探究、尝试、讨论和推理等过程，锻炼了发散性思维.这就要求教师在教学过程中，经常让学生探索各种动态变换的规律，并作大胆而合理的猜想和推理，力求在培养学生创新意识和探索精神上获得新的突破，有效地训练和发展学生的发散性思维和创新思维.

认知冲突教学是数学课堂中的一道风景线，引领着课堂不断走向灵动、精彩，牵引着学生不断走向灵性、智慧.教师如何有效利用认知冲突来实现课堂的有效性、情趣性和发展性是衡量教师专业水平的重要标尺.在实践中，教师既要精确把握认知冲突的规律、内涵，又要精心设计认知冲突教学策略.教师要尽量给学生创造平等、和谐、民主的学习环境，善于激发学生的学习动机，根据学生的认知结构、智力水平和教学内容，采用不同的教学策略，激发学生的认知冲突，调动学生学习的主动性和积极性，提高新授课的教学效率.当然，这也给教师的备课带来了更大的难度，对教师的教学能力和教学水平提出了更高的要求.所以教师在教学过程中需要不断地总结和完善这方面的经验，不断创造认知冲突教学时机，不断探索认知冲突教学策略，使学生在数学海洋中畅游，使课堂在动感旋律中升华.

[参考文献]

[1]

斯滕伯格.认知心理学[M].北京：中国轻工业出版社，2006.

[2]陈兴长.创设问题情境，引导探究学习[J].福建基础教育研究，2009（5）.

[3]许国泰.“尝试原理”在初中数学教学中的应用[J].中小学数学杂志社，2010（1-2）.