增加后依然是个长方形

冒金彬

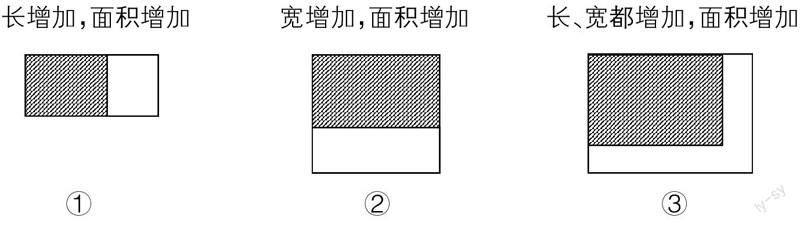
在实际生活中，经常遇到要把一块长方形的地（如花圃、操场）的长或宽增加，使这块地变大的情况。其实，不管是长增加，宽增加，还是长和宽都增加，增加的是一个面，也就是说，是将原来的小长方形变成一个大一些的长方形。这三种情况，我们可以用下面的图来表示。下面，我们来看一个实际问题。

星光小学操场宽32米，在扩建校园时，把操场的宽增加了8米，于是面积增加了360平方米。现在的操场面积是多少平方米？

很显然，这道题属于上面说的第②种情况，我们可以画图（如右下图）来帮助理解。

从图中很容易看出增加的“360平方米”是用原来长方形的长乘8得到的，也就是说，原来的长是360÷8=45（米），而现在操场的宽是32+8=40（米），所以现在操场的面积是45×40=1800（平方米）。当然，在计算出原来的长之后，也可先求出原来操场的面积是45×32=1440（平方米），再加上增加的面积360平方米，得到现在的面积是1440+360=1800（平方米）。

大家可不要小看这个简单的图示，有了它，数量间的关系变得清晰了，解答这道题也变得容易多了。而且，有了这个图形，我们还能够发现新的解法。像这道题中，阴影长方形与增加的长方形长相等，宽32米正好是8米的4倍，因此阴影长方形的面积是360×4=1440（平方米），这样，我们就可以算出现在的操场面积是1440+360=1800（平方米）。怎么样，这个方法比刚才的方法还要简便吧！

再看一个实际问题吧。

人民公园有块长方形草坪，长60米，宽40米。绿化改造时，将草坪的长增加了20米，宽增加了10米。这块草坪的面积增加了多少平方米？

显然，这道题属于上文说的第③种情况，长和宽都增加了。我们同样可以画图（如右图）来帮助理解。

求草坪增加的面积，我们可以用草坪现在的面积（60+20）×（40+10）=4000（平方米）减去原来的面积60×40=2400（平方米），求得增加的面积是4000-2400=1600（平方米）。当然也可以看成是几个小长方形面积的和：40×20+60×10+20×10=1600（平方米）。我们还可以把小长方形①和③看成一个整体，用它的面积（40+10）×20=1000（平方米）加上小长方形②的面积60×10=600（平方米），同样能够得到增加的面积是1000+600=1600（平方米）。这道题，还可以把小长方形②和③看作一个整体来做，想想看，这时应该怎么列式呢？

小朋友，你发现这种图示的魅力了吗？