确定平面内n个点所在正多边形的一种方法

牛立尚

[摘 要]本文给出了确定平面内n个点所在正多边形的一种方法，不管这n个点各自异边，还是若干点同边，只要它们构成一个凸包围，就可以用这种方法确定它们是否在某一个正多边形上，如果是，则能够给出该正多边形的顶点。

[关键词]正多边形；凸包围；自洽

[DOI]10.13939/j.cnki.zgsc.2015.07.135

1 引 言

2013高教社杯数学建模[1， 2]竞赛C题中，有一个问题是，根据古塔每层的八个数据点，确定各层的中心位置。参赛队大多数的做法是牵强地假设古塔为八角塔，且数据点位于古塔的棱角上，这些假设显然是不合适的。

利用本文的方法，可确定该题中所给八个数据点在地面上的投影点不在正四、六边形上，并计算出了投影点所在的正八边形的顶点。另外，给出了一组五个数据点，用该法计算出了它们所在的正五边形的顶点。

2 相关概念

（1）正多边形内角角度：每个内角的角度为[SX（]（M-2）π[]M[SX）]。

（2）自洽：如果穿过1点的多边形的边（称为边1）方向已知，则穿过2点的边（称为边2）的方向也将“几乎已知”：两条边要么是同一条边，要么所成的角为内角[SX（]（M-2）π[]M[SX）]；若边2的方向已知，则依同样的方法能确定边3；依次类推，如果边M的方向与边1也满足以上要求，那么这个直线方向序列就能够围成一个正多边形（称这一系列方向自洽）。

3 算法的详细步骤及计算过程

3.1 对输入n点进行顺时针排序

使得输入点按照顺时针方向存入结果数组R中。

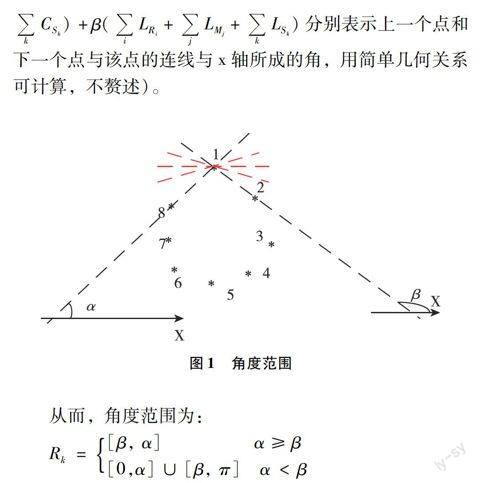
3.2 计算穿过每个点的直线方向的取值范围

给定第1个节点的斜率，递推地，可得所有节点的斜率，相应得到各个直线与x轴所成角，形成AngleBiTree。

根据AngleBiTree每个节点对应的角、斜率范围Rk，可判断AngleBiTree中该节点对应的直线角是否合法，若合法，将IsOkBiTree的相应节点置为1，否则置0。

3.4 遍历IsOkBiTree，寻找一条节点值都是1的路径

3.5 在第一条直线方向角取值范围内采样，对每个采样，执行4，并判断各方向角是否自洽

若自洽，则4中路径对应的各方向角为正多边形各边的方向角，否则用下一个采样点执行4。若最终找不到自洽的直线序列，则需要更改边数M。

4 实验结果

5 结 论

实验和理论均表明，本文给出的算法能够找到给定的一些点所在的正多边形，但很显然，这样的多边形有时不唯一，若想找到这些点能够确定的所有多边形，可穷举边1的角度初值，找到所有自洽的多边形。而实际应用中，这种方式是不必要的。例如，可选择靠近多边形顶点的一些点作为给定点，此时能够找到符合实际要求的多边形。

参考文献：

[1]赵静，但琦.数学建模与数学实验[M].北京：高等教育出版社，2003.

[2]姜启源，谢金星，叶俊.数学模型[M].北京：高等教育出版社，2011.

[3]严蔚敏.数据结构[M].北京：清华大学出版社，2007.