线性规划法在物流管理中的应用

2015-05-30曾琢

中国市场 2015年7期

关键词：线性规划运筹学物流管理

曾琢

[摘要]运筹学是物流管理的基础学科，物流管理中的许多问题都可以通过运筹学中的线性规划法加以解决。本文通过对物流领域中常见问题的研究，对线性规划法在物流管理中的进一步运用做了一些思考。

[关键词]运筹学；线性规划；物流管理

[DOI]10.13939/j.cnki.zgsc.2015.07.024

1 物流系统与线性规划

物流系统是由运输、仓储、包装、装卸搬运、配送、流通加工，物流信息等各环节要素所组成的，要素之间存在有机联系并具有使物流总体合理化功能的综合体。物流系统作为社会经济大系统的一个子系统具有输入、转换及输出三大功能，物流系统运行的主要目标包括服务目标、快速及时目标、节约目标、规模优化目标以及库存调节目标。

线性规划法作为运筹学中理论最完善、方法最成熟、应用最广泛的一个分支，通过运用数学方法和工具，对所研究的问题求出最优解，寻求最佳的行动方案，实现统筹规划和各项资源的组织、筹划和调度，所以它也可看成是一门优化技术，提供的是解决各类问题的优化方法。线性规划所研究的问题主要有两类：一类是已给定一定数量的人力和物力资源，如何用这些资源完成最大量的任务；另一类是已给定一项任务，如何统筹安排，才能以最小量的资源去完成这项任务。即有关“多、快、好、省”的最优化问题。而物流系统实现高效运行以及克服系统中各要素的制约关系等问题都需要运用到线性规划方法来解决，因此二者相辅相成，互相促进。

为了有效地降低物流配送的成本，在时间、运输路线、仓储量等多目标下的物流储运成本的控制就成了关键的问题。运用线性规划的统筹学原理，将物流配送基于时间、路线的成本管理问题转化为线性规划数学模型，通过对模型的求解，使得物流配送的利益最大化有解；然而，构建不同的线性模型，所采用的算法的不一，也会对物流配送的最佳解产生直接的影响，因此，有必要对物流配送问题进行算法的比较研究，以期能够获得最接近于实际情况的模型，所求得的解具有一定的通用性。

2 线性规划法在物流管理中的应用

2.1 库存管理和控制问题

主要应用于解决多种物资库存量的管理，确定某些设备的能力或容量，如某仓库库存能力的大小，某港口码头的转运能力，车载量的大小等，这类问题的实质是通过目标函数的建立实现仓储资源的充分利用。

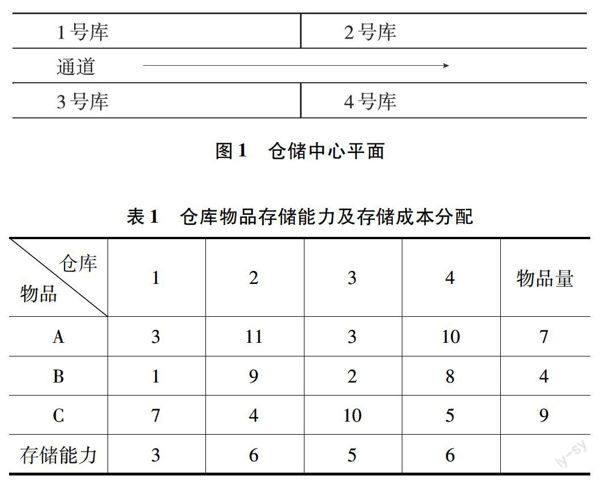
例如：某市新建一物流仓储中心，其平面图如图1所示，现有一批货物准备存入该物流仓储中心，具体有三种物品A、B、C，其量分别是7、4、9。已知各仓库存储能力及存储成本如表1所示，考虑到不同仓库存储能力、管理费用、入库成本，在总存储成本最小的前提下，分配三种物品。

解：

根据线性规划理论与方法，将仓库视为销地，货物视为产地，货物总量20，仓储总量20，将问题转化为一个产销平衡的线性规划问题，建立模型解得A物品存储5个单位在3号库，2单位在1号库；B物品存储3各单位在4号库，1个单位在1号库；C物品存储6个单位在2号库，3个单位在4号库。此时，得到最优的仓库分配方案，其存储费用为：3×1+6×4+5×3+2×10+1×8+3×5=85。

2.2 运输问题

这一问题历来是物流管理研究问题的重中之重，它包括了空运、水运、公路运输、铁路运输、管道运输以及内部物流、第三方物流的运输问题等。空运问题涉及飞行航班和飞行机组人员服务时间安排等，水运有船舶航运计划、港口装卸设备的配置和船到码头后的作业安排，公路运输除了汽车调度计划外，还有公路网的设计和分析、最优路径的选择、司机的调度安排、行车时刻表的安排、运输费用的合理定价、车场的设立等一系列问题，都可以借助线性规划法予以解决。

例如：某运输公司接受了向抗洪抢险地段每天至少运输180吨的支援物资的任务，该公司有8辆载重为6吨的A型卡车和4辆载重为10吨的B型卡车，有10名驾驶员。A型卡车每天可往返4次，B型卡车每天可往返3次，每辆A型卡车每天往返成本为320元，B型为504元，问如何调配车辆，使公司成本最低？

2.3 配送问题

随着现代物流的发展，配送逐步成为物流中的一个重要组成部分，同时由于配送并不单单只是一个相对独立的物流功能，它从一产生起就表现出了相当强的综合性。从某种意义看，一个大型的物流配送中心几乎就是一个微缩的全过程物流，因此配送过程中涉及的运筹学问题也更多更复杂。比如货物分拣搭配、货配车、车配货、人员调度安排、库存空间分配等。

现代物流配送网络大多分为两级，各个大区再根据情况可划分为若干个小区，为降低运输成本和仓储成本，明确层次和关系以方便管理，对于物流配送网络来讲，一般有如下要求：

（1）为了方便网络中货物配送的运输和管理，所有货物必须从本层次的货物始发点发出，其他节点相互问不存在货物调配运输，这样，简化了物流配送网络，又避免了运输能力的浪费。

（2）货物即使在运输途中经过其他节点，也不调用途经节点的库存，故可以认为网络中同一层次的任何节点都是直接与本层次的货物始发节点相连通的。

（3）为了降低仓储成本，提高仓储效率，即各节点尽量降低仓储量，存储的货物只满足当地市场的需求，在情况允许的时候，甚至可以出现短时间少量缺货。

（4）货物从发货点到各个节点的运输方式和运输线路有多种方案可供选择，但对于特定物流网络中的某一货物来说，根据运输要求和市场需求的不同（如要求最短时间或最小费用），运输的相对最优方案是存在的，而且一段时间内比较稳定，物流配送网络中的运输能力是有限的，所以，发送物品量应当不大于物流配送网络的运输能力。

例如：某配送中心要配送两种货物，第一种货物单位价值3万元，单位体积2立方米，单位重量1吨；第二种货物单位价值4万元，单位体积3立方米，单位重量1吨，车辆的额定载重量为5吨，额定载重容积为8立方米，两种货物批量都为3吨，试用线性规划方法进行车辆配载，使车辆装载价值最大。

2.4 物流节点选址决策问题

这类问题主要解决优化物流中心以及其他物流节点的布局安排，增强物流节点布局的合理性，以最少的物流节点辐射尽可能大的物流活动区域，增大物流节点建设实施的可行性。

例如：某配送中心有三个备选地，供应商2个，客户3个，相关参数如表2所示，用线性规划方法进行选址决策。

目前，以计算机为手段，应用运筹学、数理统计等方法和系统理论，已成为支撑现代物流管理的有效工具，相信在物流管理系统中，运筹学与信息技术的有效结合，将使物流管理上升到一个更高的水平。

参考文献：

[1]任志霞.物流配送系统中的运筹学问题及其方法研究[J].物流科技，2007（3）.