例谈2015年高考试题中概率与其他知识点的交汇

文/王博蓉 文丹

一、概率与平面几何的交汇

例1:(2015年湖北卷理数)如图1，在圆心角为扇形OAB中，分别以OA，OB为直径作两个半圆。在扇形OAB内随机取一点，则此点取自阴影部分的概率是 ()。

解题思路:不妨设扇形OAB半径为2。如图1，记两块白色区域的面积为S1，S2;两块阴影部分面积为S3，S4;则S1+S2+S3+S4而S1+S3=S2+S3的和恰好为一个半径为2的圆的面积，即① - ②得S3=S4。由图可知所以S阴影=πa2-2a2。由几何概型概率公式可得，此点取自阴影部分的概率

二、概率与立体几何的交汇

例2:(2015年湖南卷理数)四面体的一个顶点A和各个棱的中点共10个点

(1)从其它顶点与各棱中点中取3个点，使它们和点A在同一平面上，不同取法有多少种?

(2)从中任取4个点，则这4个点恰好不共面的概率是多少?

解题思路:(1)(直接法)如图2，含顶点A的四面体的3个面上，除点A外都有5个点，从中取出3点必与点A共面共有中取法，例如从D、B、H、O、J中任取3个点必共面。含顶点A的三条棱上各有三个点，它们与所对棱的中点共面，共有3种取法，例如A、B、D、J必共面。根据分类计数原理，与顶点A共面三点的取法有+3=33种。

三、概率与线性规划的交汇

例3:(2015湖北卷理数)在区间［0，1］上随机取两个数x，y，记p1为事件的概率，p2为事件”的概率，p3为事件的概率，则 ()。

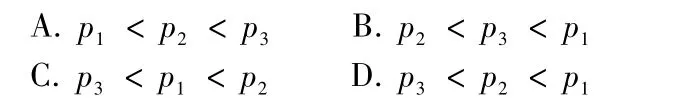
因为S△ABO=S△BEG=S△DGF=S△ACF，所以p2〈 p3〈 p1，故选B。

四、概率与复数的交汇

例4:(2015年陕西卷理数)设复数z=(x-1)+yi(x，y∈R)，若，则y≥x的概率为 ()。

总之，在高考数学试卷中越来越重视在知识网络交汇处设问，这不仅考查各知识点本身内容，而且加强知识之间的联系，体现知识的整体性和关联性。可以说，今年高考概率题与线性规划、复数的交汇，是一种创新，它进一步拓展了概率与其它知识的联系，优化概率知识框架，有利于学生创新意识的培养，是素质教育落实到教学的良好体现。