基于Simulink的转差频率矢量控制的建模和仿真

2015-05-29彭景金蒋程江园园

电气开关 2015年5期

彭景金，蒋程，江园园

(1.雷勃电气(苏州)有限公司，江苏苏州 215400;2.华北电力大学，北京 102206)

1 引言

常用的电机变频调速控制方法有电压频率协调控制(即V/F比为常数)、转差频率控制、矢量控制以及直接转矩控制等［1］。其中，矢量控制是目前交流电动机较先进的一种控制方式，它又有基于转差频率控制的、无速度传感器和有速度传感器等多种矢量控制方式。采用这种控制方法可以使调速系统消除动态过程中转矩电流的波动，从而在一定程度上改善了系统的静态和动态性能，同时它又具有比其他矢量控制方法简便、结构简单、控制精度高等特点［2］。

矢量控制是目前交流电动机的先进控制方式，一般将含有矢量交换的交流电动机控制都称为矢量控制，实际上只有建立在等效直流电动机模型上，并按转子磁场准确定向地控制，电动机才能获得最优的动态性能。转差频率矢量控制系统结构简单且易于实现，控制精度高，具有良好的控制性能、因此，早起的矢量控制通用变频器上采用基于转差频率控制的矢量控制方式。基于此，本文在Mtalab/Simulink环境下对转差频率矢量控制系统进行了仿真研究。

2 转差频率矢量控制原理

转差频率控制控制思想就是从根本上改造交流电动机，改变其产生转矩的规律，设法在普通的三相交流电动机上模拟直流电动机控制转矩的规律。

异步电动机的基本方程式［3］为:

式中:i1r、i1m分别为转子电流的转矩分量和励磁分量;Lm、Lr分别为定、转子电感;Ψr为转子总磁链;ωs为转差角频率;Tr为转子时间常数;Te为电磁转矩;np为异步电动机的磁极对数;P为微分算子;L1m为定子绕组漏感。

电气传动控制系统均服从以下基本运动方程:

式中TL为负载转矩，J为电动机转子和系统的转动惯量。

由式(6)可知，要提高系统的动态特性，主要是控制转速的变化率显然，通过控制Te就能控制因此调速的动态特性取决于其对Te的控制能力。

电动机稳态运行时，转差率s很小，因此ωs也很小，转矩的近似表达式为:

式中:Km为电动机的结构常数，Φm为气隙磁通，R2'为折算到定子边的转子电阻。

只要能够保持Φm不变，异步电动机的转速就与ωs近似成正比，即控制ωs就能控制 Te，也就能控制，与直流电动机通过控制电流即可控制转矩类似［4］。

3 转差频率矢量控制系统构建

转差频率控制的异步电动机矢量控制调速系统的原理图如图1所示。该系统主电路采用了SPWM电压型逆变器，这是通用变频器常用的方案。转速采用了转差频率控制，即异步机定子角频率ω1由转子角频率ω和转差角频率ωs组成(ω1=ω+ω)，这样在转速变化过程中，电动机的定子电流频率始终能随转子的实际转速同步升降，使转速的调节更为平滑。

系统的控制部分由给定、PI调节器、函数运算、二相/三相坐标变换、PWM脉冲发生器等环节组成。其中给定环节有定子电流励磁分量im*和转子速度n*。放大器G1、G2和积分器组成了带限幅的转速调节器ASR。电流电压模型转换由函数Um*、Ut*模块实现。函数运算模块ws*根据定子电流的励磁分量和转矩分量计算转差s，并与转子频率想加得到定子频率ω1，再经积分器得到定子电压矢量转角 θ。模块 sin、cos、dq0/abc实现了二相旋转坐标系至三相静止坐标系的变换。dq0/abc是输出是PMW发生器的三相调制信号，因为调制信号幅度不能大于1，在dq0/abc输出后插入衰减环节G4。在模型调试时，可以先在此处断输出和PMW发生器的三相调制输入信号幅值小于1的要求，计算G4的衰减系数。

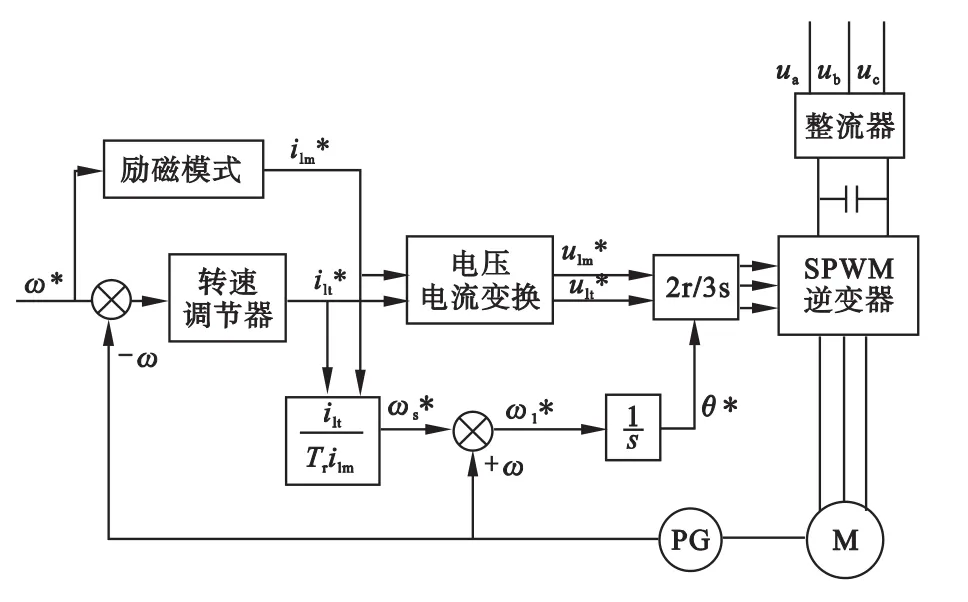
图1 转差频率控制的矢量控制系统原理框图

4 转差频率矢量控制系统仿真

4.1 仿真模型

采用电动机作为仿真对象，转差频率矢量控制系统的仿真模型如图2所示。

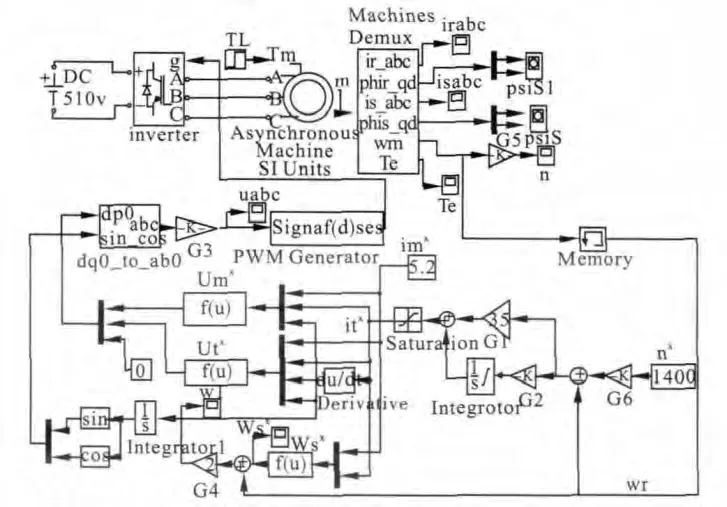
图2 电动机转差频率矢量控制系统的仿真模型

转子磁链模型的计算参数设置:异步电动机的容量为746kW、电压220V、平率50Hz、极对数为 np=2，定子绕组电阻Rm=0.435Ω，Lm=0.004mH，转子绕组电阻 Rr=0.816Ω，转子绕组漏感 Lm=0.004mH，Lm=0.069mH，J=0.19kg·m2，逆变器直流电源为 510V，定子绕组电感为LS=0.071mH，LR=0.071mH，漏磁系数为0.056，Tr=0.087。其中，G1、G2、G3、G4、G5、G6 的放大倍数分别为 35、0.15.、0076、2、9.55、1/9.55。

仿真定转速为1400r/min时的空载启动过程，在启动后0.45s时加载T1=65N*M。

4.2 仿真结果

电机在起动和加载过程中，转速、电流、电压和转矩的变化过程分别如图3～5所示。

图3 电动机的转速波形

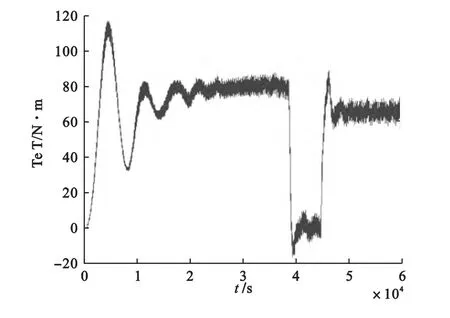
图4 电动机的转矩波形

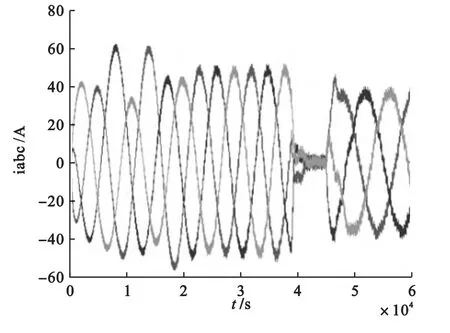
图5 电动机的定子电流

图3中可以看到，转速随时间的变化逐渐增大。当t=0.36s时，转速达到额定转速1400r/min左右，而当t=0.5s时，由于此时电动机开始加载，所以使得转速有所波动，随后趋于稳定。图4中，在加载后电动机转矩也随之增加，达到给定值Te=80N·m。图5显示，电机空载起动达到稳定转速时，电流值下降为起动电流20A。而电动机加载后，电流迅速上升，随后维持在左右。