基于卡尔曼滤波的柔性负荷预测与调节模型

张皓，裴勉，肖凡，谢金芝

(1.三峡大学电气新能源学院，湖北 宜昌 443000;2.新能源微电网湖北省协同创新中心，湖北 宜昌 443000)

1 引言

近些年，随着智能电网建设的推进以及需求响应、能效管理等技术的发展与应用，使得用户侧负荷的弹性特征逐步呈现，形成了新的可调度资源——柔性负荷，为地区电网调度运行带来了新的变化。柔性负荷是指能够改变用电时间或负荷大小以配合电力运行商的需求响应策略从而获得经济效益的负荷，主要包括可中断负荷和激励负荷，其具有的响应快、经济性高和体现不同用户用电意愿等优点使之日益受到学者关注［1－8］。因此可以通过充分利用智能电网的新技术和新装备，进一步研究柔性负荷参与地区电网调度运行的关键技术。

基于卡尔曼滤波的负荷预测在不少文章中都有所介绍和研究［9－11］。然而有柔性负荷参与的负荷预测和调节研究及建模的文章却很少，本文初步探讨了有柔性负荷参与的预测和负荷调节的策略和模型。

2 卡尔曼滤波介绍

卡尔曼滤波器是一个“最优化自回归数据处理算法”。对于解决大部分的问题，它是最优，效率最高甚至是最有用的。其广泛应用已经超过30年，包括机器人导航，控制，传感器数据融合甚至在军事方面的雷达系统以及导弹追踪等。近年来更被应用于计算机图像处理，列入，面部识别，图像分割，图像边缘检测，负荷预测等方面。

2.1 卡尔曼滤波的数学模型

首先要引入一个离散控制过程的系统，该系统可用一个线性随机微分方程来描述:

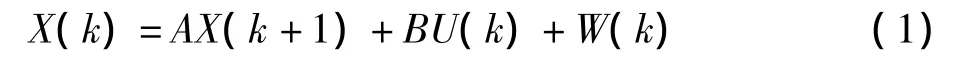
再加上系统的测量值:

上两式子中，X(k)是k时刻的系统状态，U(k)是k时刻对系统的控制量。A和B是系统参数，对于多模型系统，它们为矩阵。Z(k)是k时刻的测量值，h是测量系统的参数，对于多测量系统，h为矩阵。W(k)和V(k)分别表示过程和测量的噪声。它们被假设成高斯白噪声，其协方差分别是Q，R，这里假设它们不随系统状态变化而变化。

由于满足上面的条件(线性随机微分系统，过程和测量都是高斯白噪声)，卡尔曼滤波器是最优的信息处理器。下面来估算系统的最优化输出。

首先利用系统的过程模型预测下个状态的系统。假设现在的系统状态是k，根据系统的模型，可以基于系统的上一状态而预测出现在状态:

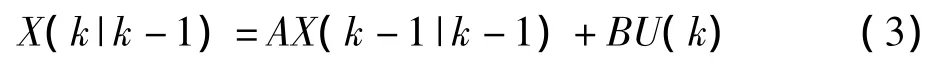
式(3)中，X(k|k－1)是利用上一个状态预测的结果，X(k－1|k－1)是上一个状态最优的结果，U(k)为现在状态的控制量，如果没有控制量，它可以为0。

到现在为止，系统结果已经更新了，可是对应于X(k|k－1)的协方差还没有更新。用P表示协方差:

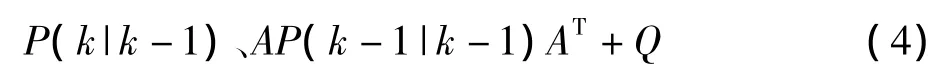
式子(4)中P(k|k－1)是X(k|k－1)对应的协方差，P(k－1|k－1)是 X(k－1|k－1)对应的协方差，AT表示A的转置矩阵，Q是系统过程的协方差。式(3)、式(4)就是卡尔曼滤波器5个公式当中的前两个，也就是对系统的预测。

有了现在状态的预测结果，再收集现在状态的测量值。结合预测值和测量值，可以得到现在状态(k)的最优化估算值X(k|k):

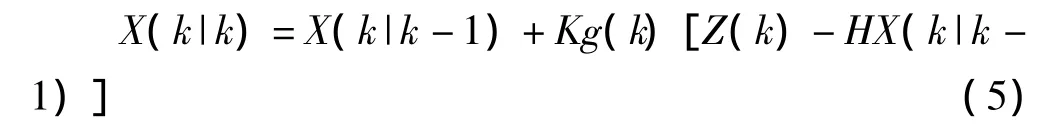
其中Kg为卡尔曼增益:

到此为止，已经得到了k状态下最优的估算值X(k|k)。但是，为了要令卡尔曼滤波器不断地运行下去，直到系统过程结束，还要更新k状态下X(k|k)的协方差。

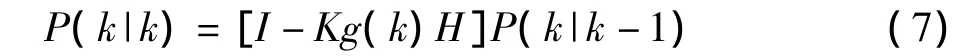
其中I为单位矩阵，对于单模型单测量，I=1。当系统进入式(k+1)状态时P(k|k)就是式(4)中的P(k－1|k－1)。这样，算法就可以自回归地运算下去。

卡尔曼滤波器的原理基本描述了，式(3)～(7)是5个基本公式。根据这5个公式，可以很容易地实现计算机程序。

2.2 卡尔曼滤波的图形解释

卡尔曼滤波的本质思想是这样的:它以k－1时刻的最优估计X(k－1|k－1)为基准，依据负荷预测系统的状态方程，预测时刻的状态向量X(k|k－1)，在这一过程中又要对状态值进行观测，通过观测获得观测向量Z(k)，最后通过观测量和获得的预测量之间进行误差分析，也可以看作把观测量当作预测值的一个修正参考，最终获得K时刻最佳的状态估计值X(k|k)。

卡尔曼滤波算法过程可以用平面上的点线图来表示，下图就是从k－1时刻开始到k+2时刻结束工作过程示意图。

图1 卡尔曼算法过程平面点线图

◇代表由卡尔曼滤波得到的预测负荷，★代表经过卡尔曼滤波得到的最优估计负荷，Δ代表测量负荷。BC线段代表k时刻从量测中得到的新息ε(k)=z(k)－x(k|k－1)，BD线段代表K时刻增益矩阵与新息乘积Kg(k)·ε(k)，即对预测负荷的修正量。

卡尔曼滤波的流程是:每隔一个滤波周期，通过得到的量测负荷C，同时经过状态转移得到预测负荷B，在量测负荷与预测负荷之间根据增益Kg(k)进行折中，从而获得最佳估计负荷D，依次过程不断循环下去。

对卡尔曼滤波和负荷预测图作如下分析:

如果不存在系统干扰W(k)，也不存在量测噪声V(k)，这时图中的B和C点重合在一起。

(1)如果只存在系统干扰而不存在量测噪声，那么，增益矩阵K就是一个单位矩阵，通俗的说就是把获得的有用信息不作折中处理直接对负荷预测进行修正。此时，图中的D点和C点是重合的。

(2)如果只存在量测噪声而不存在系统干扰，那么图中D和B是叠在一起的。

(3)如果系统的状态噪声比较大而量测噪声相对较小，这样增益矩阵几乎等于1，平面点线图中的D点就会逼近C点。

(4)如果状态噪声比较小而量测噪声大，这时候增益矩阵接近0，图中D点靠近C点。

(5)增益矩阵的折中作用。

将增益矩阵代入滤波方程(参见公式5)并化简得:

可见，最佳状态估计x(k|k)实质上是预测估计x(k|k－1)和量测值z(k)的线性加权的组合，加权系数由预测误差方差和量测误差方差的大小决定，即增益矩阵的作用是在预测量和量测量之间进行折中处理。

3 柔性负荷参入调度调节

3.1 调节过程

柔性负荷参入调度调节的过程如图2所示。

图2 柔性负荷参入调度调节的过程示意图

首先是负荷数据采集，这里的数据包括历史数据和当前的实时数据。然后对采集到的数据进行各种分析，挖潜出柔性负荷的调度潜力，然后以此为依据，制定控制策略和执行控制策略，最后对控制效果进行评价，如果调节效果不理想的下次可以进行优化。

3.2 控制策略

各个地区的柔性负荷特性都有所不同，只有对各个地区的负荷特性有深入了解的基础之上才能对柔性负荷进行有针对性的调控，达到良好的调节效果。

一般而言在非峰谷时段没有必要进行柔性负荷的调控。在负荷波峰期应该减少柔性负荷，在负荷波谷期可以增加柔性负荷。这就是所谓的削峰填谷。

本文提到的柔性负荷参与调控策略的数学模型如下式

其中Preal表示当前实发有功;Puplimt是负荷波峰警戒值;Pdownlimt为负荷波谷警戒值;ε是随机误差;η是负荷可调节率。n和柔性负荷可调节量有关。

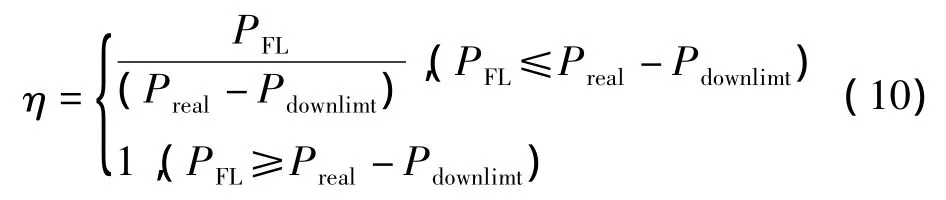
其中PFL为可调节的柔性负荷量。

4 案例分析

对某地区某天的日负荷行仿真计算，分别进行没有柔性负荷参入的日负荷曲线和有柔性负荷参入的负荷曲线仿真计算。

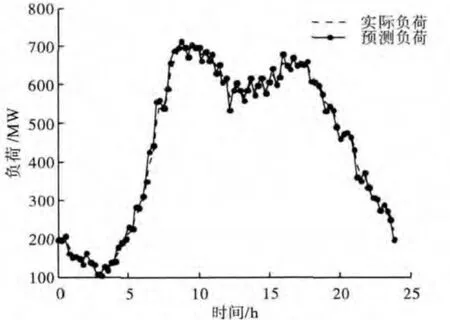
图3 日负荷曲线

利用卡尔曼进行负荷预测的结果如图3所示。由图可知预测负荷和实际负荷很接近，这也表明了卡尔曼滤波预测负荷算法的有效性。

卡尔曼滤波模型中有项，也就是控制项，传统的卡尔曼滤波的负荷预测中该项为0，然而有柔性负荷之后，对负荷进行调节也就成为可能。该项的作用和影响就不能够忽略了。可以根据柔性负荷调节策略进行调节。根据上节内容的柔性负荷调节策略进行仿真对比的结果如图。

5 结束语

“互动性”是智能电网的重要特征之一，柔性负荷的出现为互动性带来可能，柔性负荷必将作为一种系统资源参与到电网的运行管理中去，并成为一种重要的电网运行调节手段。建立合理的柔性负荷模型是进行柔性负荷实用化计算的前提。本文建立的基于卡尔曼滤波的模型既能进行负荷预测，也能够进行负荷控制。经过仿真计算表明该模型预测效果良好，并且柔性负荷能够做得削峰填谷。

图4 有无柔性负荷参与调度调节的负荷对比曲线

［1］姚建国，杨胜春，高宗和，等.电网调度自动化系统发展趋势展望［J］.2007，31(13):7－11.

［2］杜贵和，王正风，等.智能电网调度一体化设计与研究［J］.电力系统保护与控制，2010，38(15):127－131.

［3］林榕，王永红，张会贤，等.智能调度一体化系统在河北南网的应用［J］.电力系统保护与控制，2012，40(2):151－155.

［4］Young Min Wi，Ji Hui Kim，Sung Kwan Joo，etc.Customer Baseline Load(CBL)Calculation using Exponential Smoothing Model with Weather Adjustment.IEEE T＆D Asia，2009.

［5］赵鸿图，朱治中，于尔铿.电力市场中用户基本负荷计算方法与需求响应性能评价［J］.电网技术，2009，33(19):72－78.

［6］牛文娟，王磊，李扬.需求响应项目中用户基线负荷计算方法及其应用［J］.东南大学学报，2014，44(3):556－560.

［7］曲大鹏，伍伟华，江迪，等.基于径向基神经网络的需求侧响应用户基线负荷计算方法［J］.理论与算法，2014，4:26－30.

［8］杨楠，王波，刘涤尘，等.计及大规模风电和柔性负荷的电力系统供需侧联合随机调度方法［J］.中国电机工程学报，2013，33(16):63－69.

［9］王科，陈丽华.基于卡尔曼滤波的节假日短期负荷预测［J］.电气技术，2014，01:4－6.

［10］李江，王义伟，魏超，等.卡尔曼滤波理论在电力系统中的应用综述［J］.电力系统保护与控制，2014，06:135－144.

［11］陈军，陶巍，吕英飞，等.基于卡尔曼滤波的短期负荷预测［J］.电气开关，2014，2:43－45.