220kV输电线路风偏数值模拟研究
2015-05-29杨秀友
杨秀友
(国网武汉供电公司,湖北 武汉 430000)
1 引言
随着国民经济的快速发展,我国对电力能源的需求逐渐增长,国家电网公司加快了对输电线路的大规模建设[1],然而由于输电线路是长期暴露在自然界的人工构筑物,因此其在风力作用下发生风偏现象对输电线路的安全运行影响极大。
国内外很早就开展了关于输电线路风偏现象的研究,例如文献[2]就以一起大同电网发生的较为罕见的220kV线路两相风偏掉闸故障为例,对引起输电线路发生风偏现象的多方面原因进行了分析和探讨,依据分析的结果和建议提出了输电线路预防和抑制风偏的一些措施和策略。关于输电线路风偏故障应对措施方面的研究,文献[3]结合一些输电线路跳闸统计情况从风偏发生的机理、天气、地理环境、线路本体设计等多方面原因综合分析了风偏故障的成因,依据风偏防治的原则和规范给出了相应的风偏故障防范措施,并结合相关的电网事故案例对输电线路风偏防治的现行状况提出了进一步的整改措施。由于输电线路会频繁发生风偏闪络事故,因此文献[4]分析了风偏闪络的特点和原因,从风偏角计算中分析各因素对计算值的影响,结果表明风速、风压不均匀系数、风向与导线轴向夹角以及风压高度变化系数都对风偏角有不同程度的影响。风速是输电线路风偏现象主要的影响因素,文献[5]认为输电线路在强烈大风影响下导线会发生严重的不同期摆动导致导线相间距离减小甚至发生相间击穿,对输电线路的运行产生了极大的威胁,因此采用了一个3自由度多档动态模型来对输电线路的不同风速的风偏动态特性进行研究,并找到抑制大风不同步摆动的有效方法。风偏计算对于保障输电线路安全运行具有十分重要的意义,文献[6]认为规范中风偏角计算的刚性直棒模型没有考虑分裂导线间的屏蔽和脉动风影响,因此采用有限元仿真的方法建立了绝缘子串-导线耦合模型,对脉动风作用下的绝缘子串风偏进行了动力时程分析,规范了风偏角计算公式。为输电线路设计提供了参考依据。关于输电线路导线风偏在线监测方面的研究,文献[7]研究了新型风偏角计算的数学模型,提出了一种新型输电线路风偏在线监测系统,该系统采用无线风偏监测仪通过上下两个风偏角结合进行计算,得出绝缘子串实际的风偏角,通过在向家坝-上海±800kV特高压直流输电工程实际运行情况表明系统能够有效指导高压输电线路运行维护管理。
本文针对输电线路风偏现象选取武汉市某220kV输电线路特征段作为研究对象,通过输电线路荷载的基础计算以及风荷载的处理建立了输电线路风荷载的数学计算理论模型,基于有限元法建立该输电线路特征段的有限元模型对输电线路风偏问题进行数值模拟,通过风偏时程分析得到风偏角的统计结果,证明风荷载调整系数随着风速的增大呈缓慢上升的趋势。
2 输电线路风荷载
2.1 输电线路风荷载数值模拟方法
风荷载是空气流动对工程结构所产生的压力,也称风的动压力,通常把自然界的风划分为脉动风和平均风,平均风随着高度的变化而产生指数规律变化,而脉动风则随着空间和时间的变化发生随机变化,本文研究的风荷载模拟对象为脉动风,工程中常用的风速功率谱为 Kaimai谱[8]:

式中,Vi为剪切速度;z0为地面粗糙长度;f为频率;z为离地面的高度。
脉动风交叉功率谱密度函数可以表示为:

由于在大气中互谱和正交谱的比值极小,因此在工程应用中将上式改写为:
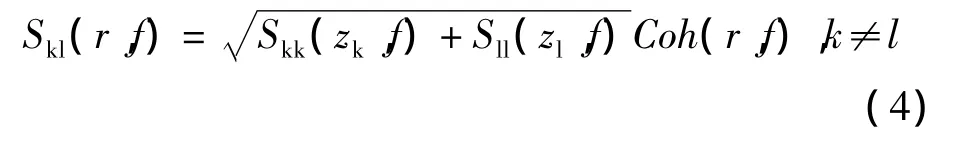
式中,Skk(zk,f)和 Sll(zl,f)为空间两点距离为 r的自功率谱;Coh(r,f)为相干函数。
由于输电线路结构体系中的脉动风荷载可以用零均值的多维高斯平稳随机过程来描述,因此可采用谐波叠加法来对其进行模拟。具有m个零均值的平稳随机过程{v1(t),v2(t),…,vm(t)}的谱密度矩阵为:

式中,ω为圆频率;Sij(ω)为功率谱函数。
将S(ω)进行分解以后可以得到:
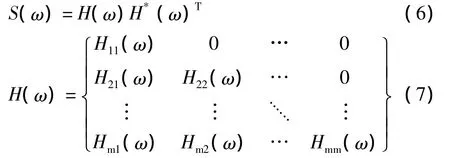
由于在实际工程应用中经常忽略正交谱,因此{v1(t),v2(t),…,vm(t)}可以通过下式进行模拟:

式中,N为充分大的正整数;Δω为频率增量;ωml为截止圆频率;Φml为均匀分布在区间[0,2π]内的随机相位角。
通过模拟得到脉动风速以后,输电线路任意一点处的风荷载可以通过下式进行快速有效地数值模拟:
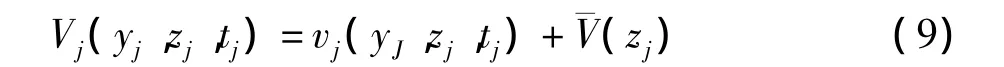
2.2 输电线路风荷载数学计算模型
风荷载的计算与基本风压、地形、地面粗糙度、距离地面高度,及建筑体型等诸因素有关。根据我国的电力行业现行标准规定,顺风方向的风荷载在输电线路风偏现象上起决定性作用,其导线上的风荷载计算式为:

式中,lH为输电杆塔的水平档距;Wx为垂直于输电线路的水平风荷载;βc为输电线路导线作用于杆塔上的风荷载调整系数;μsc为输电线路的体形系数;α为输电线路风压的不均匀系数;d为输电线路的导线外径;V为输电线路规定基准高处的设计风速;θ为风向与输电线路导线轴向之间的夹角,式中具体参数参考文献[9]。
输电线路绝缘子串的风压按下式计算,即:

式中,n1为输电线路每一相的相导线所用的绝缘子串数量;n2为每串绝缘子的片数;Ap为每片绝缘子的受风面积;Kz为风压的高度变化系数;V为计算风速。
3 220kV特征段输电线路风偏时程分析
3.1 特征段输电线路有限元模型
本文以武汉市某条典型的输电线路耐张段作为研究的对象,建立有限元理论模型如图1所示。该输电线路的耐张段线路包括两档,其两端布置为耐张塔,中间布置为无转角直线杆塔,该输电线路的导线中间通过悬垂的绝缘子串悬挂在直线杆塔上,两端则通过耐张绝缘子串连接到耐张塔上,如图2所示,图中l1和l2分别为直线杆塔两端导线的档距,h10和h20分别为直线杆塔两端导线的高度差。图3为特征段输电线路在脉动风作用下发生风偏时的状态图。
该输电线路特征段模型为双分裂导线,包括两档,在整个输电线路的有限元模型当中,输电线路的悬垂绝缘子串是由15片XP-7型号的陶瓷绝缘子连接而成。双分裂导线的子导线型号为LGJ-300/40型钢芯铝铰线,间隔棒的型号为 FJZ-300。

图1 输电线路特征段线路有限元理论模型
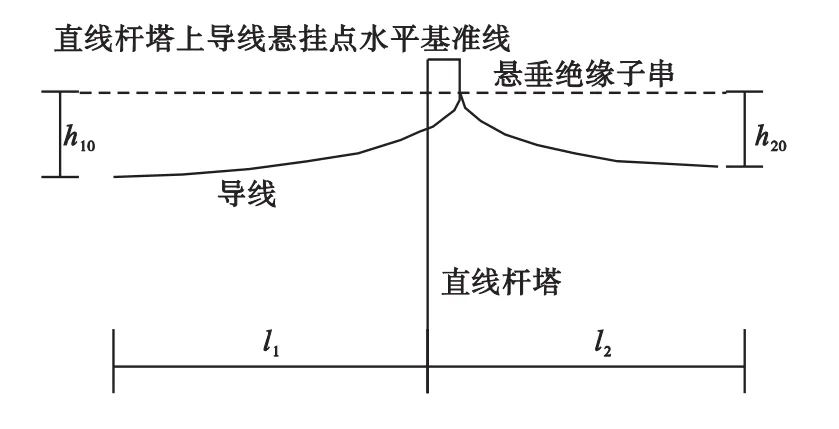
图2 输电线路的特征段模型

图3 特征段输电线路在脉动风作用下发生风偏时的状态
3.2 特征段输电线路风偏数值模拟
针对武汉市220kV特征段输电线路,按照前文关于输电线路风荷载模拟方法利用ABAQUS/CAE有限元软件建立该特征段输电线路的有限元分析模型,假设该特征段输电线路的地面粗糙系数为a=0.16,地面粗糙长度为z0=0.33,地面高度距离导线弧垂最低点位置为10m,直线杆塔两端导线的档距为300m的等档距,每隔10m模拟一次,模拟时程为500s,模拟风速为20m/s、25m/s和30m/s。在进行特征段输电线路风偏数值模拟时,风偏角的响应时程和悬垂绝缘子串下端点的位移时程是关注的焦点,由于篇幅有限,本文仅给出了风速为20m/s时的风偏角时程曲线和绝缘子串下端点的位移时程曲线如图4、图5所示。

图4 风偏角时程曲线

图5 绝缘子串下端点的位移时程曲线
4 风荷载调整系数的讨论
现行输电线路的设计规程中计算其悬垂绝缘子串的风偏角的计算方法没有考虑到风的脉动性对输电线路导线及其绝缘子串上的动力作用的影响,即输电线路导线及其绝缘子串的风荷载均没有计入风荷载的调整系数βC中。根据目前关于输电线路的现行设计规程,不考虑实际环境中脉动风影响时的风偏角的正切计算公式为:
式中,PI=Wx/lH;GI为绝缘子串重力;W为导线单位长度自重力;T为导线中的张力;q为塔位高差系数。

当q=0,即无高位差时的风偏角正切表达式为:
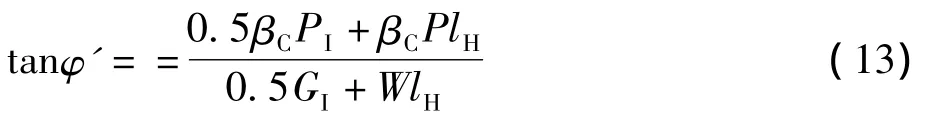
此时可推导出风荷载调整系数:

式中,φ'是考虑风的动态特性后的风偏角。

由此计算出3中基本风速的风荷载调整系数如表1所示,从表1可以看出在考虑实际环境中脉动风影响时风荷载调整系数随着风速的增大呈缓慢上升的趋势,因此可以发现现行输电线路设计规程中关于风偏角计算方法存在不足。

表1 特征段输电线路悬垂绝缘子串的风偏角统计
5 结论
本文通过输电线路荷载的基础计算以及风荷载的处理建立了输电线路风荷载的数学计算理论模型,选取武汉市某220kV输电线路特征段作为研究对象,建立该输电线路特征段的有限元模型对输电线路风偏问题进行数值模拟,通过风偏时程分析得到风偏角的统计结果,证明风荷载调整系数随着风速的增大呈缓慢上升的趋势。
[1]刘振亚.智能电网技术[M].中国电力出版社,2010:1-8.
[2]赵文元,杨保东.输电线路风偏故障的预防和抑制[J].电力学报,2004,19(1):66-68.
[3]武国亮,宋述停,等.输电线路风偏故障应对措施[J].水电与新能源,2013,6:28-31.
[4]龙立宏,胡毅,等.输电线路风偏放电的影响因素研究[J].高电压技术,2006,32(4):19-21.
[5]孙保强,侯镭,等.不同风速下导线风偏动力响应分析[J].高电压技术,2010,36(11):2808-2813.
[6]李黎,肖林海,等.特高压绝缘子串的风偏计算方法[J].高电压技术,2013,39(12):2924-2932.
[7]黄新波,陶保震,等.采用无线信号传输的输电线路导线风偏在线监测系统设计[J].高电压技术,2011,37(11):2350-2355.
[8]祝贺,徐建源.基于多点卡曼谱输入的输电塔脉动风数值模拟[J].华东电力,2008,36(9):18-21.
[9]国家电力公司东北电力设计院.电力工程高压送电线路设计手册[M].2版.北京:中国电力出版社,2003:103-327.
