基于改进遗传算法的无刷励磁系统参数估计

沈峰

(康泰斯(上海)化学工程有限公司，上海 201203)

1 引言

当发电机的励磁电流大于8000A时，由于受到滑环材质、炭刷均流等因素的影响，制造相应容量的滑环是困难的，为此，大型汽轮发电机采用无刷励磁系统是适宜的［1］。美国西屋公司(Westinghouse)在上世纪60年代研制出大型汽轮发电机无刷励磁系统，经过近半个世纪的发展如今已经成为大型汽轮发电机的主要励磁方式。

电力系统运行、调度的基础是数字仿真，仿真的结果可信度依赖于模型结构及其参数的准确性。AC1A模型是IEEE提出的三机交流励磁系统的标准模型，同时他励或自励无刷励磁系统也多以此作为标准模型结构。参数辨识就是在系统结构以知的条件下通过对系统输入输出信号的处理和分析确定系统组成各个环节的参数也称为参数估计。基于系统辨识的参数估计有丰富的理论支持和研究基础，以最小二乘法为代表的参数辨识在很多领域得到应用［2］。但是这种方法只适用于线性系统的参数估计。无刷励磁系统由于其显然的非线性环节，传统的线性系统参数辨识方法得到的结果无法接受。基于模型响应与实测响应最好拟合的参数估计在激励信号满足系统可辨识性的条件下可以不区分所研究系统的线性与非线性［3］，选择合适的优化算法在一定范围内总能找到一组最优的参数使得模型响应与实测响应最好的拟合。

遗传算法由于其固有的并行处理以及全局寻优能力在优化领域得到众多应用［4］。本文在简单实数编码遗传算法基础上对交叉算子进行改进，使交叉后产生的两个子代都是可行解，并且必有一个子代靠近较好的父代，从而使得解向好的方向发展。利用改进后的遗传算法进行无刷励磁系统各环节参数估计结果证明算法的收敛性和精度较简单遗传算法均有提高。

本文研究了包含非线性环节的无刷励磁系统参数估计优化算法;建立有效的参数估计工业试验方法。文章首先详细描述了IEEE的AC1A励磁模型，利用Matlab/Simulink搭建待辨识励磁系统模型以及单机仿真系统，分别施加M序列伪随机信号和机端电压阶跃信号对待辨识系统进行激励，采用改进遗传算法辨识励磁系统参数。

2 无刷励磁系统模型

无刷励磁系统由于主励磁机采用与发电机转子绕组同轴的旋转电枢同步发电机和旋转整流装置，使得励磁电流可以无需电刷滑环直接介入转子绕组。根据励磁控制器控制对象不同，无刷励磁可以分成两类一种是采用旋转二极管整流装置，控制器通过控制主励磁机的励磁电流控制主励磁机端电压;另一种是采用旋转晶闸管的全控整流装置，励磁控制直接控制晶闸管导通角获得需要的励磁电流。后者由于励磁控制信号不经过交流励磁机所以具有极高的响应速度，但是制造上难度较大。工业中采用较多的是前者。图1是IEEE提出的ACIA励磁模型也是Westinghouse公司的主流无刷励磁系统模型［5］。图中机端电压VC与电压参考值Vref在信号叠加点获得电压差值，经AVR的超前滞后环节和综合放大环节后形成励磁调节信号VR(主励磁机励磁电压)，通过主励磁机环节形成空载电势VE。考虑整流环节的换相阻抗以及不同负载电流的影响最后得到同步发电机励磁电压Efd。图中略去了励磁系统中的保护环节如低励限制等。

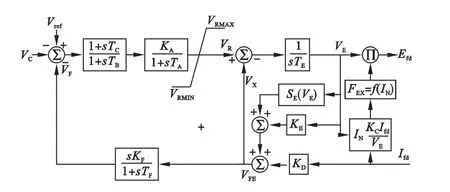
图1 无刷励磁系统框图

式(1)表示整流器的三个不同工作状态

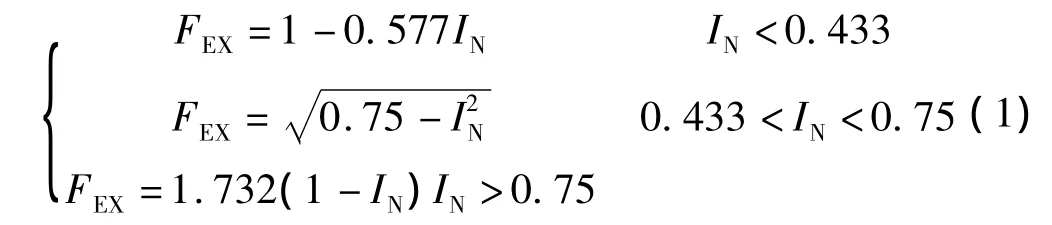
同时AC1A模型考虑了交流励磁机的磁饱和以及电枢反应的去磁效应，这使获得同样的VE实际的励磁机励磁电压Vfe要比不考虑饱和及去磁效应时的励磁电压大。饱和系数SE是空载电势VE的函数，常见的表达如(2)式:

KD反映了交流励磁机的电枢反应，其值由主励磁机的直轴同步电抗电及暂态电抗决定。电压软反馈环节通过加入微分环节提高空载运行是励磁调节器的稳定性，其输出VF在信号叠加点上。

3 基于改进遗传算法的参数估计

一旦选定模型结构，系统辨识过程就进入参数估计阶段。基于模型响应与实测响应最优拟合的参数估计常采用如下目标函数:

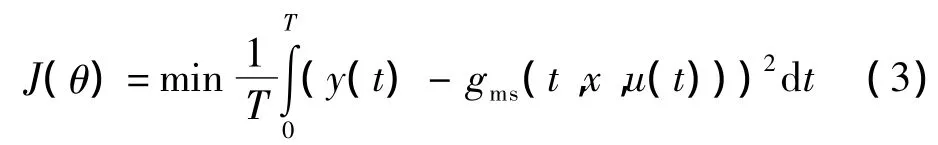
离散化后得到:

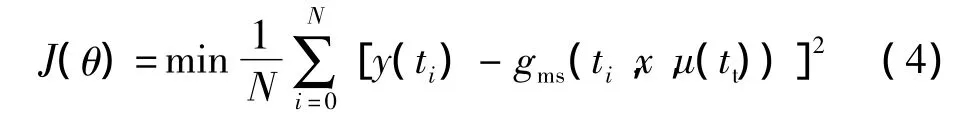
式中y(t)是实测系统输出，x为待估计参数组，gms(t，x，u(t))是模型输出，其中 u(t)是输入信号(激励)。T是参数估计试验周期，离散化后转化成数据长度N。

上述目标函数的极小化问题是一个非线性优化问题，必须采用非线性优化算法来解决，基于现代优化算法的非线性优化问题的求解得到关注并取得一定的成果［6－7］。

3.1 改进遗传算法

遗传算法(Genetic Algorithm，GA)是一种基于自然群体遗传演化机制的高效探索算法。它将问题域中的可能解看作是生物群体的一个个体或染色体，并将每一个体编码成符号串形式，根据预定的适应度函数对每个个体进行评价，针对参数估计的遗传算法适应度函数可以表示为:

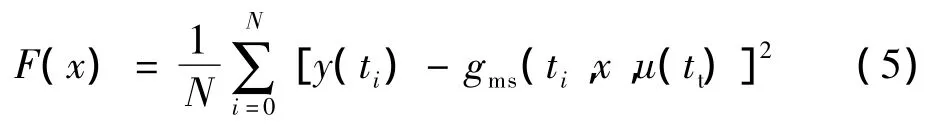
通过对群体反复进行基于遗传学的操作(选择，交叉和变异)，依据优胜劣汰的进化规则，不断得到更优的群体，以全局并行搜索方式来搜索优化群体中的最优个体。因在求解连续参数优化问题时，实数编码的遗传算法比二进制编码的遗传算法的收敛速度快且精度高，本研究针对无刷励磁参数估计的优化问题对各环节参数采用实数编码，针对简单遗传算法交叉算子的弊端改进交叉算子。本算法中选择算子采用适应度值比例选择法(也称轮盘赌法)。变异操作采用均匀变异，即简单地在指定范围内随机选一个实数替代原基因。对于交叉算子做如下改进:

交叉运算的基本概念源于凸集理论。对于个体(染色体向量)的如下组合:

按对乘子限制的不同，可获得凸交叉和线性交叉。凸交叉要求 λ1+λ2=1，λ1＞0，λ2＞0;如果仅要求乘子属于实数空间，则成为线性交叉。凸交叉使得后代过于集中而线性交叉使得后代过于分散，可能产生不可行解。假设，种群大小pop=m，个体长度为n，交叉概率为pc，从第t代个体中根据交叉概率随机选择两个个体:

xr={x1r，x2r，…，xrn}，xs={x1s，x2s，…，xsn}进行交叉操作，其中(1≤r，s≤m)，两个个体中进行交叉的基因为xri，xsi，(1≤i≤n)，，交叉操作后对应基因为 x'ri，x'si，(1≤i≤n)。

(1)如果个体xr优于个体 xs，即 F(xr)＞F(xs)，则

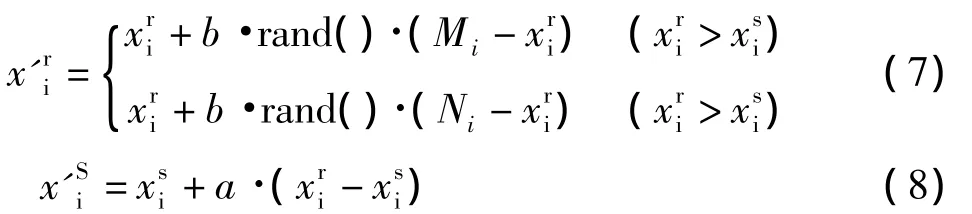
(2)如果个体xs不劣于个体xr，即F(xr)≤F(xs)则:

这样的交叉操作可以确保一个后代靠近较好的父代，且可消除不可行解，大大加快收敛速度。

3.2 基于改进遗传算法的参数估计流程

Step1 建立模型并确定待估参数，根据实际情况确定各个参数的上下限值，采用实数编码建立遗传算法解空间，确定个体适应度函数;

Step2 确定遗传算法的控制参数值如群体规模，最大迭代次数;

Step3 初始化种群;

Step4 执行遗传操作;

Step5 如果满足停止准则则输出结果，否则继续执行Step4。

4 无刷励磁系统参数估计的试验设计

图2是仿真试验系统单线图。

图2 单机仿真系统

其中工频60Hz，发电机采用六阶凸极机，原动机与调速器，变压器负荷等系统组成部分的详细参数参见文献［8］。励磁系统结构框图如图1，其中TB、TC为超前滞后环节时间常数，本仿真模型中设置为零不作辨识。待估计的线性环节参数包括励磁调节器放大倍数和时间常数Ka、Ta，励磁绕组的时间常数，励磁电压软反馈环节参数Kf、Tf。非线性环节中需要辨识的参数包括饱和环节及电枢反应环节的参数A、B、KE、KD以及换相阻抗系数KC。

4.1 参数辨识试验设计

在图1的无刷励磁系统中包含有线性环节与非线性环节，本研究对线性环节与非线性环节分别进行辨识。首先利用幅值可调的M序列伪随机信号做激励，当发电机带75%额定负荷时，在参考电压Vref(Vref=1)处施加M序列伪随机信号［9］。记录机端电压Vt、励磁电压Efd、励磁电流Ifd。饱和环节线性化为饱和系数SE+KE仿真中取实际值，反映电枢反应的系数KD取实际值，整流器工作在第一种工作状态，即FEX=1－0.577IN整个环节等效成一个与励磁电流的线性函数，仿真中取实际值，只辨识 KaTa、Te、Kf、Tf，其真值见表1。仿真中施加的M序列伪随机信号引起的Vt变化在0.5%之内，其具体参数为:幅值a=0.001，采样周期:Δt=0.001s，信号长度:N=511，重复周期数:q=8。仿真中各量均用标么值。

工业试验中一般利用阶跃响应来考察系统的动态特性，同时利用试验的激励与响应数据进行励磁系统参数辨识。考虑到对系统的冲击，试验时间比起利用伪随机信号进行得辨识试验稍长。阶跃信号的加入点也是参考电压Vref处，在1s时加入0.05标么值的阶跃，4s时加入－0.05的阶跃，总仿真时间7s。仿真用的模型参数线性环节参数采用利用伪随机信号辨识得到的参数，仅辨识非线性环节参数A、B、KE、KD以及换相阻抗系数KC其真值见表2。

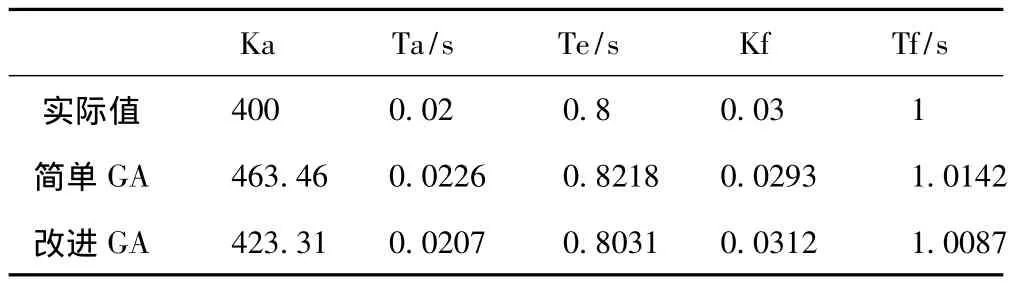
表1 线性环节参数辨识结果

4.2 辨识结果

本文的参数辨识算法采用改进遗传算法(IGA)，其中迭代次数50，群体规模100。分别施加M序列伪随机信号和参考电压阶跃信号，输出响应信号Efd、Ifd的采样频率均为1000Hz。辨识结果如表1、2所示。由辨识结果可以看出改进遗传算法地辨识精度高于简单遗传算法。图3分别为改进遗传算法辨识得到的线性模型输出Efd与实测Efd拟合曲线以及非线性模型Efd与实测Efd拟合曲线。为了验证模型的泛化能力采用0.1s发生0.2s恢复的发生于230kV母线处的三相短路扰动来对比实测Egd与模型Efd输出，从图4拟合曲线可以看出模型输出与实测拟合地非常好。

图3 不同采样频率下的实际与辨识系统的响应

表2 非线性环节参数辨识结果

图4 大扰动仿真与实测响应

5 结论

无刷励磁系统的详细模型包含非线性环节，本文提出线性环节与非线性环节分别辨识，采用不同的辨识信号利用改进遗传算法获得了很好的辨识结果。

［1］S.M.L.Kabir，R.Shuttleworth，“Brushless exciter model”，IEE Proceeding，Generation，Transmission，Distribution，1994，141(1):61－67.

［2］Jin-Cheng Wang，Hsiao-Dong Chiang，Chiang-Tsung Huang，et al.I-dentification of excitation system models based on-line digital measurement［J］.IEEE.Trans on power systems，1994，10(3):1286－1293.

［3］Eric.ludwig，M.L.Crow，Kelven.Ericson，et al.A feasibility study of on-line excitation system parameter estimation ［J］.IEEE.Trans on power systems，1998，13(3):910－916.

［4］李敏强，寇纪凇，林丹，等.遗传算法的基本理论应用［M］.北京:科学出版社，2002.

［5］IEEE committee report.proposed excitation system definitions for synchronous machines［R］.IEEE Trans on power apparatus and systems，Vol.Pas－88:1248－1258，1969，8.

［6］贺仁睦，王卫国，蒋德斌，等.广东电网动态负荷实测建模及模型有效性的研究［J］.中国电机工程学报，2002，22(.3):78－82.

He Renmu，Wang Weiguo，Jiang Debin，et al.Measurement-based dynamic load modeling and model validation on Guangdong grid［J］.Proceedings of the CSEE，2002，22(3):78－82.

［7］沈峰，贺仁睦，王君亮，等.基于非线性直接优化方法的发电机励磁系统参数辨识［J］.电网技术，2007，31(8):73－77.

［8］IEEE Working Group on Prime Mover and Energy Supply Models for System Dynamic Performance Studies，“Hydraulic Turbine and Turbine Control Models for Dynamic Studies，”IEEE Transactions on Power Systems，February，1992，pp.167－179.

［9］沈善德.电力系统辨识［M］.北京:清华大学出版社，1993.