基于插值法波面拟合的球面光学元件检测

郭巧双，王 敏，廖晓东

（福建师范大学 光电与信息工程学院 医学光电科学与技术教育部重点实验室，福建 福州350007）

引言

目前国内外干涉仪如Zygo干涉仪、移相式数字波面激光干涉仪等对干涉图样进行波面拟合采用的都是Zernike多项式拟合算法［1－2］，但是直接影响拟合精度的Zernike多项式的阶数较难确定［3］，文献［4］中则定性地说明了Zernike多项式边界误差对拟合结果存在影响，在文献［5］中，采用对干涉图分别进行行插值和列插值，再将两次的插值结果进行加权拟合出干涉图的波面，但仍存在的问题就是由于插值法不具有Zernike多项式的单位圆正交性质，不能限制插值边界，边界存在突变，给计算结果带来一定的误差且计算速度慢。随着径向基理论的发展，径向基函数已经广泛应用于大地测量学、神经网络、自由曲面重构等领域，在实际应用当中很多类型的径向基函数都能得到很好的结果，尤其是以multi－quadric函数（简称MQ函数）为基底函数的径向基函数在散乱数据插值中可以得到理想的结果［6］，因此根据一般球面光学元件基本为圆形孔径［7］，本文先采取最小二乘法对数据边界点进行拟合得到边界圆［8］，确定出数据边界点的中心和半径值，并用样条插值确定边界波像差，解决由于边界数据少，误差大的问题；然后用multi－quadric函数插值法对已知数据直接进行插值拟合，既能克服Zernike多项式的阶数不易确定的问题，又可在不需要确定波面方程的情况下，直接给出任意指定点的波像差，进而还原出波面，计算出波面峰谷偏差EPV值及均方根偏差ERMS值。

本文主要是在Matlab软件平台上，分别对国标干涉图、Zygo干涉仪采集的干涉图进行拟合，并将拟合结果所得的面形偏差与国标面形偏差、Zygo干涉仪检测的面形偏差进行对比。由于美国Zygo公司的GPI系列干涉仪，其测量结果得到 国 内 外 同 行 的 公 认［1－2，9］，因 此 本 文 方 法 的 拟 合精度主要通过与Zygo干涉仪测量结果比较为准。

1 图像处理过程

干涉图样通过裁剪、格式转换、双臂旋滤波等预处理后，通过Otsu方法的最佳全局阈值处理进行图像分割，提取出干涉图样的明（暗）条纹，再通过数学形态学细化算法提取明（暗）条纹的骨架得到干涉条纹中心线，由于骨架提取后存在毛刺，采用形态学方法对骨架的毛刺进行去除，避免对波面拟合引进误差，接下来通过级次标定，即可确定每条明（暗）条纹的相位为2nπ或光程差为nλ［10］。最后通过已知的相位或光程差对波面进行插值拟合。图像处理步骤见图1，国标干涉图中马鞍形光圈（文献［10］附录B.9）处理结果如图2所示。

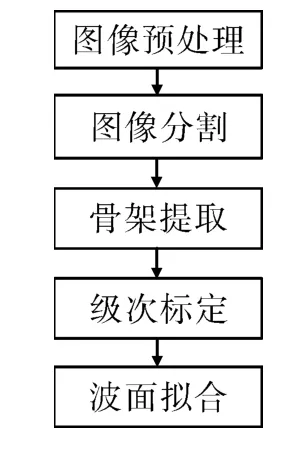
图1 图像处理步骤Fig.1 Image processing steps

图2 处理后的干涉条纹Fig.2 Preprocessed interferogram

2 边界处理

由于Zernike多项式是互为正交、线性无关的，而且可以唯一地、归一化描述系统圆形孔径的波前边界，所以在Zernike多项式波面拟合过程中不需要考虑边界问题。而插值法拟合波面不具有自然约束边界的条件，故必须考虑边界问题.基于一般球面光学元件都是圆形孔径［7］，且非闭合型的干涉条纹的端点位于干涉图样的边界，所以边界的处理主要根据非闭合型干涉条纹的端点来拟合边界圆，并根据已知数据点的波像差拟合出整个边界圆的波像差，即可实现对插值边界进行约束。

2.1 查找干涉条纹的端点

根据干涉条纹提取的骨架为单像素宽度的图像，则在骨架像素中8邻域范围内只存在1个像素点的像素为骨架的端点（如图3所示，中心像素a即为端点）。根据端点定义通过扫描遍历各个像素点确定其8邻域的像素个数即可查找出干涉条纹骨架的端点。

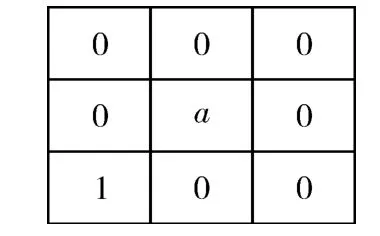
图3 中心像素a为端点的8邻域示意图Fig.3 8－adjacent areas with center pixel ato be endpoint

2.2 确定边界圆及边界波像差

将查找出的边界点的行索引值及列索引值作为已知边界点坐标（xi，yi），以已知边界点到拟合圆心的距离与拟合圆半径的平方差最小为拟合边界圆的判断依据，采用最小二乘法进行拟合圆，即可确定圆心和半径，拟合边界圆的结果如图4所示。过Matlab进行矩阵的左除即最小二乘法解法便可确定（D，E，F）参数使取得最小值，再根据（2）式便可确定拟合圆的参数（x0，y0，r）。

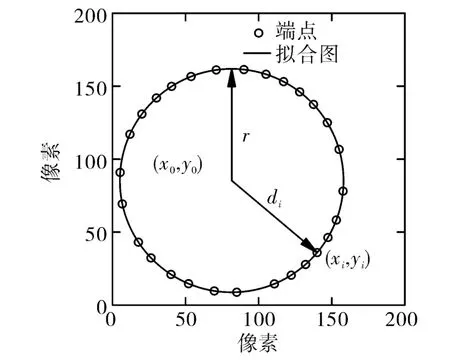
图4 拟合示意图及边界拟合圆Fig.4 Schematic diagram and boundary fitting circle

对于边界波像差，可根据圆的参数（圆心和半径）将已知边界点的坐标（xi，yi）转化成极坐标（ρ，θi），再根据已知边界点的极坐标θi及相对应的波像差zi进行一维的样条插值，采用 Matlab中interp1函数选用拟合效果较平滑的“spline”分段样条插值方法，即可得到整个边界的位置及波像差，计算出的边界波像差如图5所示。

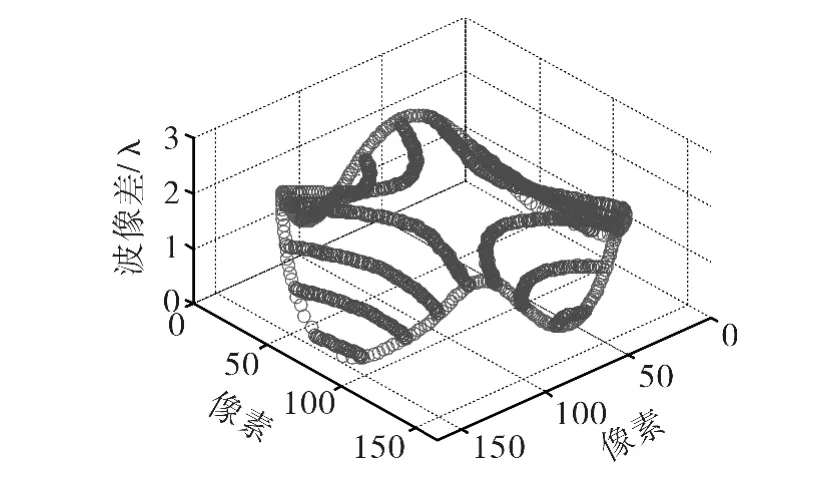
图5 边界波像差Fig.5 Wave aberrations of boundary

如图4所示已知边界点到拟合圆圆心的距离为di，拟合半径为r，根据圆的一般方程：

可得：

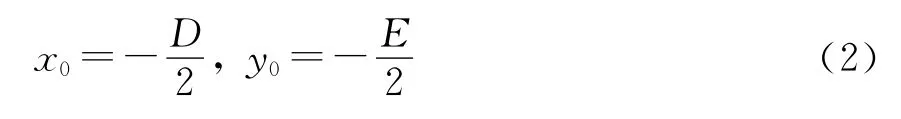
则已知边界点到拟合圆心的距离与拟合圆半径的平方差为

根据（3）式由已知边界点建立线性方程组，通

通过边界点确定边界圆的圆心及半径的大小即可确定插值的有效范围，因为插值中存在外插偏差大问题，通过插值拟合确定边界波像差既可减小外插带来的影响，又可以增加采样点提高波面拟合精度。

3 MQ函数插值

MQ 函数的表达式［12－14］为

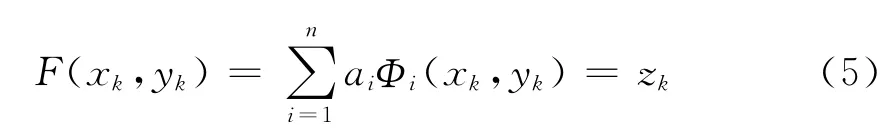
其中zk为已知点的波像差。即已知波像差的点为（x1，y1，z1），（x2，y2，z2），…，（xn，yn，zn）

其中c为形状参数。插值计算前应先用提取出的干涉条纹中心线及其对应的波像差根据先行方程组（5）式计算最小二乘法计算系数ai的值：

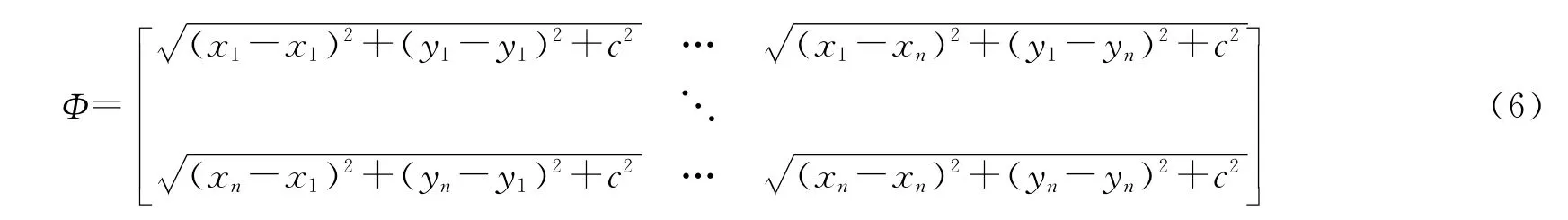
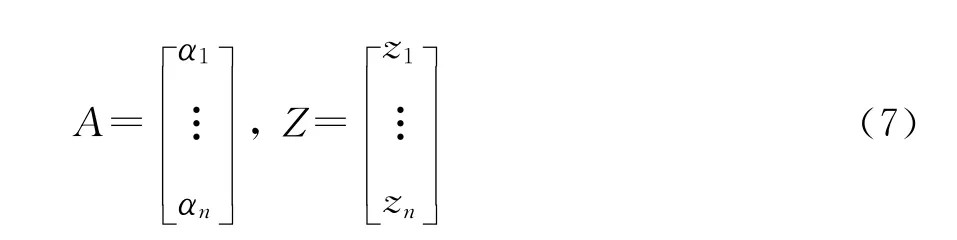
则有

即可通过最小二乘法计算得到系数向量A。

径向基为

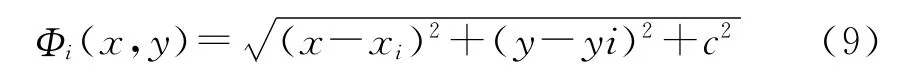
采用函数插值给定的点集，即可拟合出各个点的位相得到被测波面的轮廓。

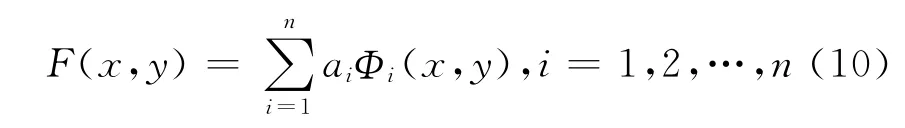
4 处理结果分析

EPV值是被测波面上相对于参考波面的峰值与谷值之差；ERMS值是被测波面相对于参考波面各点偏差值的均方根［11］。通过波面拟合结果即可得到波面相对于参考波面各点偏差值Ei，则通过（11）式便可计算出波面的峰谷偏差：

由于国家标准光圈给出的是半径偏差N，计算出的EPV值无法与国标给定的半径偏差值直接进行比较，则根据（12）式即可实现EPV与N 的转化［15］，其中λ为波长。

通过（13）式计算波面的均方根偏差ERMS：

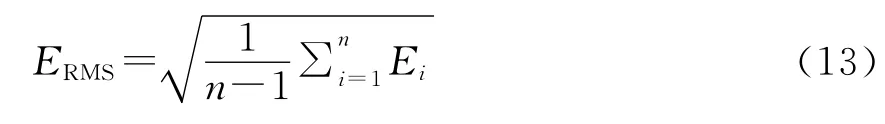
本文采用国标干涉图及Zygo公司GPI－XP／D4干涉仪采集的图片进行测试对比。图6所示图a和图b分别为国标干涉图参照文献［8］附录B.9、附录B.19测试结果的MQ插值拟合波面图。

Fig.6 国标干涉图拟合结果图Fig.6 Fitting results of national standard interferograms

计算结果如表1所示：

表1 国标干涉图测试数据Table 1 Test data of national standardinterferograms

表1给出了MQ插值方法对国标干涉图的检测结果，从国标干涉图的检测结果看，MQ函数插值方法检测出的EPV误差约为0.2λ，基本在测量误差范围内。由于国标干涉图主要是用来作为光学车间样板法定性检测的标准，精度有限，且国标图在实测中较难采集到相同的图样用于验证。因此通过ZygoGPI系列干涉仪的采集图样进行进一步验证。

图7为Zygo公司GPI－XP／D4干涉仪采集的图片的拟合结果。

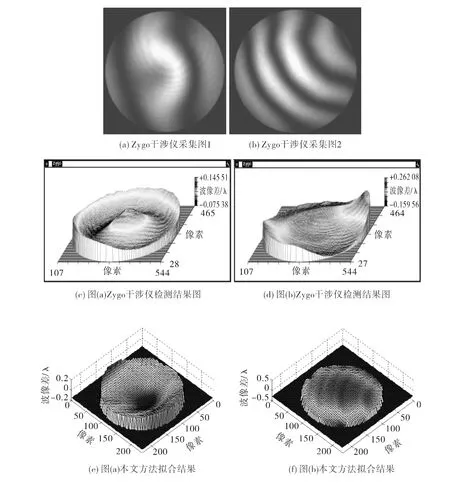
图7 Zygo干涉图拟合结果图Fig.7 Fitting results of Zygo interferograms

表2则给出了MQ插值方法与Zygo干涉仪对Zygo干涉仪采集图的检测结果，从表2有无拟合边界波像差的检测结果可得，通过边界波像差的拟合可有效地减小插值误差；从MQ函数插值方法（有拟合边界波像差）与Zygo干涉仪的检测结果比较可得，峰谷值EPV和均方根偏差ERMS差异约为0.03λ，与Zygo干涉仪的检测结果较接近，即验证了采用MQ函数插值拟合波面可基本满足非接触在线检测光学镜片的精度带求并具有可行性。

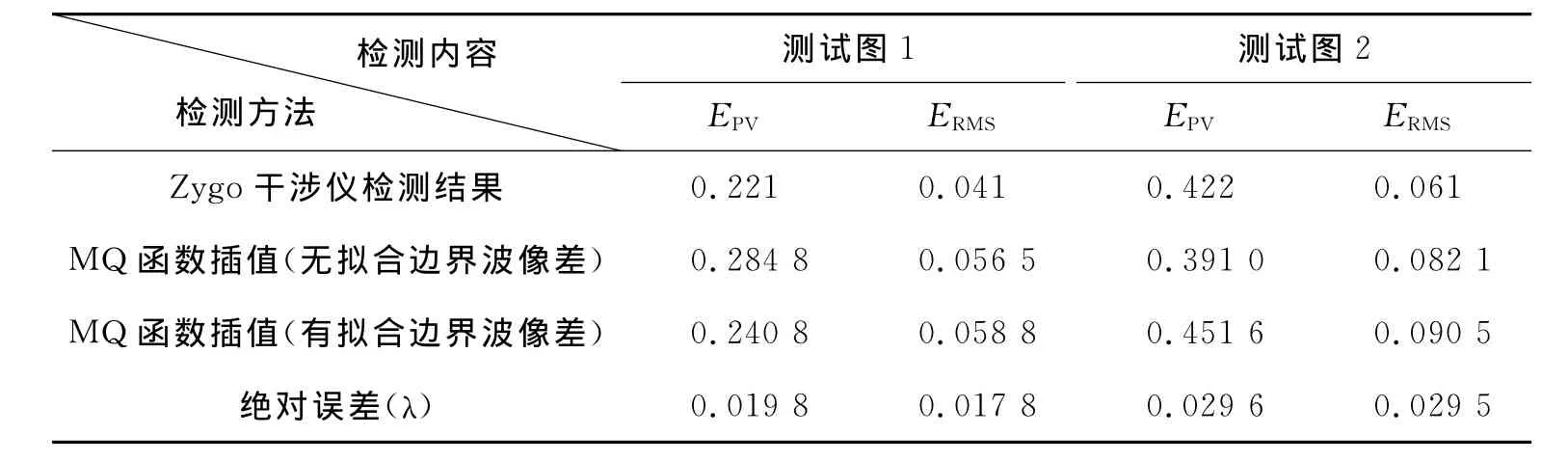
表2 Zygo干涉仪采集图测试数据Table 2 Test data of Zygo interferometer λ

5 结论

采用最小二乘法进行边界拟合可精确地确定数据取值边界点，即确定插值的有效范围；采用MQ函数插值基本实现了对干涉图波面面形的重建，且重建的波面光滑度较高；将MQ函数插值与边界波像差拟合相结合，也有效地提高了检测精度。虽然前期图像处理环节引入一定的误差，导致根据干涉条纹提取的相位信息精度有限，使得检测结果仍存在一定的误差，但是测量误差能够满足球面光学元件非接触在线检测的精度要求，且采用MQ函数插值方法与不同的边界拟合方法有望实现对椭圆形、方形孔径的光学元件进行检测。

［1］ Yu Yi.Zygo interferometer and its application［D］.Tianjin：Tianjin University，2005：21－33.于毅.Zygo干涉仪及其应用［D］.天津：天津大学，2005：21－33.

［2］ Yuan Qun，Gao Zhishan，Li Jianxin，et al.Research on techniques of fabrication and measurement about Fizeau infrared interferometer［J］.Chinese Journal of Lasers，2011，38（8）：0808001.袁群，高志山，李建欣，等.斐索式红外干涉仪研制和测试技术研究［J］.中国激光，2011，38（8）：0808001.

［3］ Feng Jie，Bai Yu，Xing Tingwen.Fitting accuracy of wavefrontusing Zernike polynomials［J］.Electro－optic Technology Application，2011，26（2）：31－34.冯婕，白瑜，邢廷文.Zernike多项式波面拟合精度研究［J］.光电技术应用.2011，26（2）：31－34.

［4］ Hou Xi，Wu Fan，Yang Li，et al.Effect analysis of edge errors in wavefront fitting with Zernike polynomials［J］.Infrared and Laser Engineering，2006，35（S2）：72－75.候溪，伍凡，杨力，等.基于Zernike多项式波面拟合中边界误差的影响分析［J］.红外与激光工程，2006，35（S2）：72－75.

［5］ Lan Mingqiang.Study of optical surface deviation detection technology based on wavefront fitting［D］.Fujian：Fujian Normal University，2013：42－46.兰明强.基于波面拟合法面形偏差检测技术研究［D］.福建：福建师范大学，2013：42－46.

［6］ Wang Tianhua，An improved radial basis function quasi－interpolation method［D］.Jilin：Jilin University，2014：3－8.王天化.一种改进的径向基函数拟插值方法［D］.吉林：吉林大学，2014：3－8.

［7］ Zhang Wei，Liu Jianfeng，Long Funian，et al.Study on wavefront fitting using Zernike polynomials［J］.Optical Technique，2005，31（5）：675－678.张伟，刘剑峰，龙夫年，等.基于Zernike多项式进行波面拟合研究［J］.光学技术，2005，31（5）：675－678.

［8］ Liu Ke，Zhou Fuqiang，Zhang Guangjun.Radius constraint least－square circle fitting method and error analysis［J］.Journal of Optoelectronics·Laser，2006，17（5）：604－607.刘珂，周富强，张广军.半径约束最小二乘圆拟合方法及其误差分析［J］.光电子·激光，2006，17（5）：604－607.

［9］ Xu Deyan.Introduction to the impression of American ZYGO company［J］.Optical Technique，1996，3：47－48.徐德衍.浅谈美国ZYGO公司印象［J］.光学技术.1996，3：47－48.

［10］AQSIQ，SAC.GB 2831－2009Surface form deviation of optical elements ［S］.Beijing：China Standard Press，2009.中华人民共和国国家质量监督检验检疫总局，中国国家标准化管理委员会.GB 2831－2009光学零件的面形偏差 ［S］.北京：中国标准出版社，2009.

［11］Sha Dingguo，Su Datu.Optical testing technology［M］.2ed ed.Beijing：Beijing Institute of Technology Press，2010：80－96.沙定国，苏大图.光学测试技术［M］.2版.北京理工大学出版社，2010：80－96.

［12］Li Yan，Bai Yufeng.The case study about multi－quadric method［J］.Journal of Inner Mongolia University for Nationalities：Natural Sciences，2010，25（4）：369－372.李艳，白玉峰.Multi－quadric函数与Gauss函数的插值比较［J］.内蒙古民族大学学报：自然科学版，2010，25（4）：369－372.

［13］Yao Yibin，Liu Jingnan，Shi Chuang，et al.Multiquadric equations interpolation and itsapplications to the establishment of crustalmovement speed field［J］.Geo－spatial Information Science（Quarterly），2002，2（5）：1－5.

［14］Tao Benzao，Yao Yibin.Parameter estimation based on multi－quadric collocation model［J］.Geomatics and Information Science of Wuhan University，2003，28（5）：547－550.陶本藻，姚宜斌.基于多面核函数配置型模型的参数估计［J］.武汉大学学报：信息科学版，2003，28（5）：547－550

［15］Cao Tianning，Bai Jian，Kong Yanbo.Application of CQG－Ⅱshop digital interferometer in several special testing cases［J］.Optical Technology，2001，27（6）：562－563.曹天宁，白剑，孔燕波.CGQ－II车间数字干涉仪的几种特 殊 检 测的 应 用 ［J］.光 学技 术，2001，27（6）：562－563.