基于PCA和kNN混合算法的文本分类方法

史淼　刘锋

摘要：随着文本数据的激增，文本分类的高复杂度是一个重要的问题。k近邻（kNN）算法是一个简单、有效，但是计算复杂度很高的分类算法。一般，在使用kNN算法时，使用主成分分析（PCA）进行预处理来减少维数，但是该算法要求投影空间中的所有向量来执行kNN算法。我们提出一个新的混合算法PCA&kNN，使用一个小的邻居集来执行kNN算法，而不是投影空间中的完整的数据向量，从而减少了计算的复杂性。 新的文本被投影到较低维的空间，kNN仅使用每个轴的邻居执行，基于更接近原始空间和投影空间且沿着投影成分的主向量。为了验证该方法的有效性，针对Reuters标准数据集进行实验，实验结果显示，新提出的模型显著优于kNN和标准PCA-kNN混合算法，同时保持了相似的分类精确度。

关键词：文本分类；降维；PCA；kNN；混合分类器；加权

中图分类号：TP312 文献标识码：A 文章编号：1009-3044（2015）10-0169-03

随着网络信息技术的快速发展和高速通信基础设施的建设，各种电子文档的数量不断增加，使得人们查找信息越来越难，为了收集有用的信息，需要对文本进行正确、有效的分类。因此，分类技术的发展越来越受到人们的重视。

文本分类是为每个文档找到正确的类，给定一组类和文本文档集合的过程，也称为监督学习，它融合了数据挖掘、信息检索、统计学、神经网络等学科的知识，主要应用于描述性问答系统、搜索引擎、推荐系统等。目前，常用的文本分类算法[1]有：支持向量机（SVM）、k近邻（kNN）、贝叶斯算法（Bayes）、遗传算法等。其中kNN算法是一种简单、有效、非参数的方法，因而得到了广泛的应用。但它有一个明显的缺点：文本的特征向量空间具有很高的维数。因此，它的计算成本很高。

现阶段，已有将主成分分析（PCA）用作kNN算法的预处理阶段，以减少维数。然而，kNN算法的计算成本尽管减少了，但仍然高，这是因为，此方法使用了投影空间中每一个向量[2]。

本文提出了一个新的混合文本分类方法，利用PCA来减少维数，同时仅对主成分中邻近的向量应用kNN算法，从而降低了kNN分类器的输入。我们证明了该混合模型能够以高精度水平分类数据，同时使用更小的主成分数从而显著减少了计算时间。

1 理论背景

1.1 文本表示

文本文档存储的是非结构化的信息，所以文本分类需要将文本表示成计算机能够处理的形式。常见的文本表示方法有布尔逻辑型、概率型和向量空间模型（SVM）[3]等。本文采用的是向量空间模型（SVM）来描述文本集。

在向量空间模型，文件被表示为向量，其中，文档中的每个条目对应于术语的权重。文本分类的一个普及的无监督的加权方式是TF* IDF（检索词频率*倒排文档频率）[4，5]。还有其他的有效监督加权方式，例如TF*RF（检索词频率*相关性频率），TF-ICF（检索词频率*逆语料库频率）[6]等。有效的文本分类取决于加权方式和分类算法两者的正确选择。

1.2 主成分分析

主成分分析（PCA）是1933年由Hotelling首先提出的，它是通过对原始变量的相关矩阵或协方差矩阵内部结构的研究，将多个变量转换成少数几个综合变量，即主成分，从而达到降维[7]的目的的一种常用的降维方法[8，9]。所谓数据降维是指通过线性或非线性映射将样本从高维空间映射到低维空间，从而获得高维数据的一个有意义的低维表示的过程。主成分的数量小于或等于原变量的数量，被用于降低高维数据的维数。

主成分分析的主要思想[10]：是设法将原来类别特征重新组合成一组新的互相无关的几个综合类别特征来代替原来类别特征，同时根据实际需要从中可取出几个较少的综合类别特征尽可能多的反应原来类别特征的信息。这种将多个类别特征化为少数互相无关的综合类别特征的统计方法叫做主成分分析。它也是常见的处理降维的一种方法。

主成分分析[11]的降维步骤如下：

1.3 kNN文本分类算法

kNN是一种分类算法[12，13]，它的基本思想[14]是：根据向量空间模型，把文本内容转化为特征空间中的加权特征向量。计算待测试文本与训练集中每个样本的相似度，找出测试文件的k个最近的邻居，并按k个邻居的类别分开统计，把测试文本划分到最相近的一类中去。

这种方法表现良好，即使在处理多分类文档的分类任务时也是一样，但是在使用大量测试样例或高维数据分类对象时，就会需要很长的时间。为了分类新到达的数据，我们需要遍历所有的测试样例来找到它的近邻。存储所有的测试样例就会引起更多的存储需求。

我们的目标是利用k近邻算法的优势，并降低它的计算复杂度。曾经提出过这样一种模式，在执行kNN算法前执行一些预处理，像PCA。通过将每个类别投影到一个主成分上。在这种情况下，一个新的向量必须被投影到多个主成分上，每个类别都有一个这样的新向量，从而增加了计算时间。他们分别计算每个类别的主成分，然后使用来自每个PCA结果中的第一个主成分。

针对上述情况，我们对上述模型[15]进行了改进，只执行一次PCA，类别的主成分数的选择也是独立的，并显示了在维持精确度的同时，显著地减少了分类时间。

2 系统架构

当用户给定一个文本数据作为输入时，混合分类算法以一个有效的方式执行分类并预测给定数据的类别。在我们处理高维数据时，PCA被用作预处理阶段。kNN预测新数据的标签。

算法A是我们执行混合文本分类的主要算法。

A. 算法——PCA分类器（）

输入：{类的训练数据集，测试数据}

输出：{测试数据的类别}

1） 计算训练数据的主成分；

2） 训练数据投影到每个主成分上；

3）测试数据投影到每个主成分上；

4）对每个投影空间执行二进制搜索，找出最近邻L；

5）计算测试数据和它在投影空间中的近邻之间的相似度；

6）选出最相似的近邻k；

7）基于已选出的近邻预测测试数据的类别。

该算法的输入是类的训练数据和测试数据。采用主成分分析（PCA）可以对高维数据降维。在投影空间中维数降低的数据被用于分类。通过在维度减少的特征空间中沿着每个主成分找到最近邻L，从而限制了kNN空间。在原始空间中聚集的数据在投影空间中也会更近，且沿着每个主成分轴。沿着主成分会有附加的近邻，但是它们不是新数据的近邻，kNN算法会丢弃它们。

图1描绘了混合算法的训练阶段。输入集包含训练数据连同它的类信息和测试数据。PCA在这里用来减少的训练数据集的特征数量。

沿着各主成分和与其对应的索引的投影的值被存储在一个二维数组中。索引稍后用于检索原始数据和投影数据，并沿着轴查找近邻。随着数组被分类，二进制搜索找到一个复杂度为O （log n）的最近邻，其中n是数组的大小。

我们的模型不仅使用PCA减少了向量的维度，而且减少了搜索空间，通过限制沿着轴线的邻居对应的数据，同时使用二进制搜索减少了发现邻居的时间。

图2显示了我们提出模型的测试阶段。当新数据到达时，我们沿着主成分投影新到达的数据。传统的kNN计算整个训练集的相似度。为了减少kNN分类的时间，我们提出了沿着各成分投影向量，并沿着主成分选择L最近邻居。这些邻居是kNN的输入数据集。而不是搜索整个训练数据和原始特征空间，因此搜索空间减小了。

一旦我们发现沿主成分最近的邻居集，kNN就会用这个有限的向量集执行，同时选出k个最近邻。基于所选子集中最相似的k个近邻预测新到达数据的类别。

我们可以基于原始向量或基于投影向量执行kNN。kNN在原始空间代价稍大，因为向量更大，但是它有更高的精确度。

3实验评估

1） 数据集

我们使用综合的且真实的数据集，Reuters 数据集，一共有6532个文档，5741个特征集，这些特征集属于52个类别。

2） 通过在综合数据集上改变样例数来进行分析

我们通过改变样例的数量，同时保持特征的数量为1000个，L为7，K为5，来测试混合分类器的执行时间。

接下来，我们比较了分类精确度，通过改变k值，分别使用投影数据和原始数据来执行我们的混合分类器的最后一步，如表1所示。正如预期的那样，使用原始数据比使用投影数据计算的相似度相对较高。对于投影数据和原始数据，k值越小分类精确度越高。

使用Reuters 数据，对传统的kNN算法，PCA预处理的kNN算法和我们提出的混合kNN算法所需时间的比较，如表1所示。我们的混合分类器表现要优于PCA+kNN方法。在用PCA预处理的kNN方法中，PCA仅用于降维。

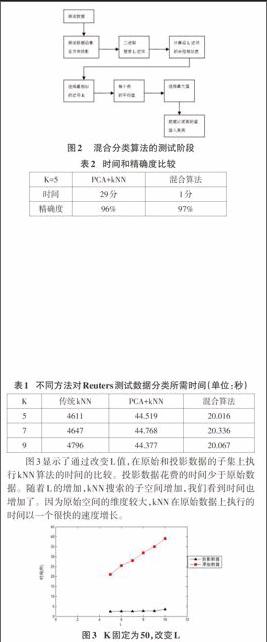
图3显示了通过改变L值，在原始和投影数据的子集上执行kNN算法的时间的比较。投影数据花费的时间少于原始数据。随着L的增加，kNN搜索的子空间增加，我们看到时间也增加了。因为原始空间的维度较大，kNN在原始数据上执行的时间以一个很快的速度增长。

使用 PCA+kNN和我们提出的混合算法进行分类，分类的精确度和所需时间如表4所示。在 PCA+kNN方法中，PCA仅仅只用于预处理步骤进行降维，然后在投影空间中执行传统的kNN算法进行分类。我们将使用Reuters 数据集的一个子集与测试数据集大小为100，训练数据集大小为6532的情况进行比较。我们的结果显示我们的混合算法在时间上有显著减少，在分类精确度上也有一些提升。

4 结束语

kNN分类器是一个很常用的高效的分类器。kNN的一个主要局限性是，当处理高维和大数据时它的分类时间问题。在这篇论文中，我们提出了一个有效的混合算法，它是基于PCA降维，和以一个新颖的方式沿着各主成分找到近邻，以便限制kNN空间并增加有效性。我们在分类时，使用了原始数据的投影空间，并表明，在使用标准的Reuters 数据集的情况下，我们的混合模型能够以很高的精确度分类数据，对kNN使用小量的主成分和更小的投影数据集。从而显著减少了计算时间。未来的工作将包括，对各种属于加权方案和传统数据集的数据分析，来了解我们混合算法的有效性。

参考文献：

[1] Han Jiawei， Kamber M， Pei Jian.数据挖掘概念与技术[M]. 范明， 孟小峰， 译. 北京： 机械工业出版社， 2012.

[2] 郭新辰， 李成龙， 樊秀玲. 基于主成分分析和KNN混合方法的文本分类研究[J]. 东北电力大学学报， 2013， 33（6）： 60-63.

[3] Christoper D M， Prabhakar R， Hinrich S.信息检索导论[M]. 王斌， 译. 北京： 人民邮电出版社， 2012.

[4] Chrles Elkan. Deriving TF-IDF as a Fisher Kernel[J]. String Processing and Information Retrieval， 2005， 3772： 295-300.

[5] Lan Man， Tan Chew Lim， Su Jian， et al. Supervised and Traditional Term Weighting Methods for Automatic Text Categorization[J]. IEEE transactions on pattern analysis and machine intelligence， 2009， 31（4）： 721-735.

[6] Reed J W， Jiao Yu. TF-ICF： A new term weighting scheme for clustering dynamic data streams[C]. 2006： 258-263.

[7] 胡煜. 基于K-紧邻法的两种降维方法应用研究[J]. 广东技术师范学院学报， 2008（6）： 35， 36-39.

[8] Jollife I T. Principal Component Analysis[M]. 2nd ed. Springer， 2002.

[9] Smith L I. Atutorial on Principal Components Analysis[R]. 2002.

[11] 张锦， 李光， 曹伍， 等.基于主成分分析的自动文本分类模型[J]. 北京邮电大学学报， 2006， 29（22）： 136-138， 143.

[12] Pawar P Y， Gawande S H. A Comparative Study on Different Types of Approaches to Text Categorization[J]. 2012， 2（4）.

[13] Aggarwal C C， Zhai ChengXiang. A Survey of Text Classification Algorithms[M]. Springer， 2012.

[14] 艾英山， 张德贤.基于文本和类别信息的KNN文本分类算法[J]. 计算机与数字工程， 2009， 37（11）： 10-12， 39.

[15] Du Min， Chen Xingshu. Accelerated k-nearest neighbours algorithm based on principal component analys[J]. Journal of Zhejiang University SCIENCE C， 2013， 14（7）： 407-416.