基于ANSYS的330kV有机复合绝缘子 表面电场建模和优化

张秀斌 牟中华 孙亚明 彭 鹏 范迪铭

（国网甘肃省电力公司电力科学研究院，兰州 730050）

近年来，电网内各电压等级的输电线路多次发生绝缘子闪络跳闸事故，对电网供电可靠性造成了重大影响，造成较大经济损失。本文基于静电场理论，采用有限元数值计算方法，建立了330kV 有机复合绝缘子的有限元模型，对有机复合绝缘子表面电场强度和电位分布进行了计算，基于计算结果提出了 330kV 有机复合绝缘子表面电场优化的措施。

早期的绝缘子电场分布研究多采用二维模型，其前提是杆塔和导线对绝缘子周围电场分布的影响很小，绝缘子周围电场主要由绝缘子自身结构和介质特性决定。研究的有机复合绝缘子的几何结构为轴对称，但由于杆塔和导线的影响，实际运行中的绝缘子周围电场具有三维特征。因此本文采用三维有限元模型对绝缘子周围电场进行计算，并考虑杆塔和导线的影响。

1 有机复合绝缘子有限元模型

本文研究的330kV 线路悬式有机复合绝缘子型号为FXBW-330/100，由两个不同厂家生产，分别标记为1#、2#。图1为有机复合绝缘子的实物图；图2为结构示意图。绝缘子高低压端均安装均压环，图3为复合绝缘子高压端均压环结构示意图（环径D、管径r、罩入深度H）。表1列出绝缘子的几何结构参数。空气、有机复合材料和环氧芯棒的相对电介质常数分别为1、2.5 和2.0。

图1 FXBW-330/100 型有机复合绝缘子

图2 有机复合绝缘子结构示意图

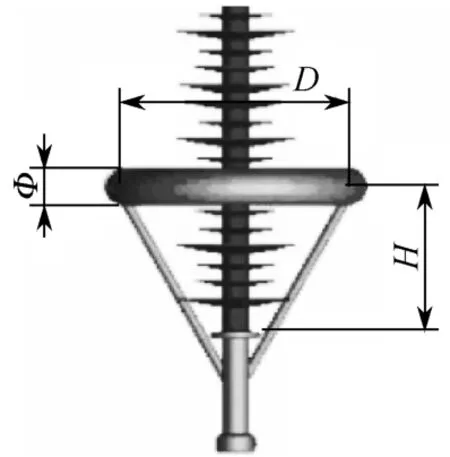
图3 有机复合绝缘子均压环结构示意图

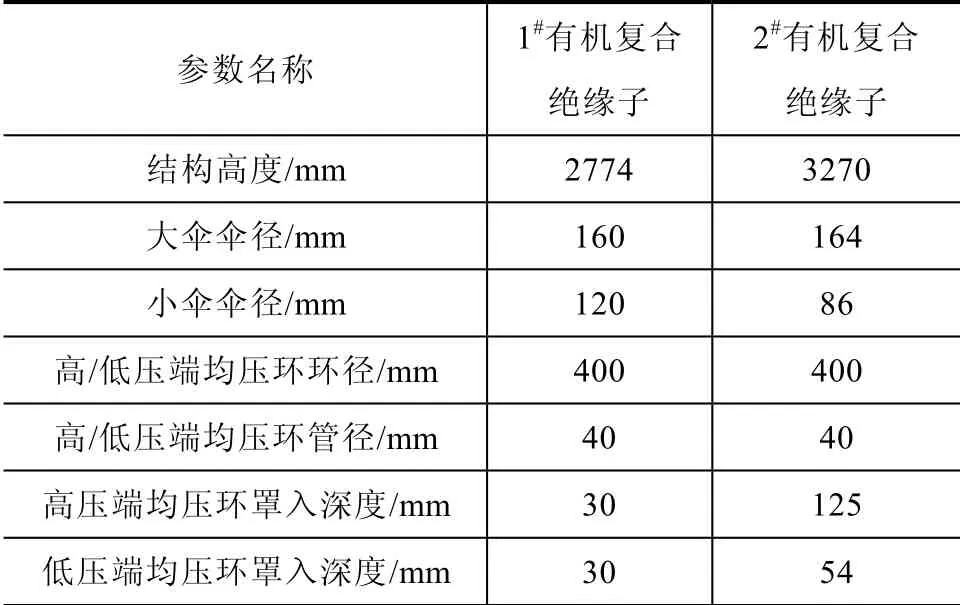
表1 有机复合绝缘子几何参数

杆塔、导线和复合绝缘子组成的三维计算电场几何模型如图4所示。其中导线为2×LGJ-400/50双分裂导线，子导线外径为 27.68mm，间隔为400mm；为减小“导线两端效应”对电场的影响，模型中导线长度取为20m[11]。杆塔模型参考330kV输电线路常用的ZMT1 型直线塔边相，绝缘子悬挂 处离地高度为25m，悬挂处距离杆塔主干6m，杆塔横担总长6.5m。

图4 有机复合绝缘子电场计算三维模型

由于有机复合绝缘子伞群结构较为复杂，所以采用一般的方法对绝缘子进行剖分，不但剖分时间长，且剖分后的有限元模型与原几何模型之间的误差较大。并且考虑到有机复合绝缘子的轴对称结构，本文选择“体-扫略”法进行剖分，即先对绝缘子纵向界面进行面剖分，再以绝缘子中心线为轴环绕整个绝缘子进行体剖分。图5所示为有机复合绝缘子剖分图。

图5 有机复合绝缘子剖分图

实际运行中的绝缘子处于大气环境中，因此可以假定绝缘子周围电场域为无界场域。本文采用零阶渐进边界条件设置人工边界将无限大范围截断为有限区域进行求解。经过优化分析和设计，将人工边界的尺寸设定为60m×30m×80m 时计算得到的绝缘子周围电场不再随场域边界的扩大而改变。

2 有机复合绝缘子的电场计算

2.1 杆塔及导线对绝缘子周围电场的影响

为定量地分析杆塔、导线对绝缘子周围电场分布的影响，分别对以下四种工况的1#有机复合绝缘子周围电场进行了计算，分别是“无导线，无杆塔”、“有导线，无杆塔”、“无导线，有杆塔”和“有导线，有杆塔”。

图6为有限元分析得到的四种情况下1#有机复合绝缘子电位云图，图7为四种情况所对应的绝缘子表面电位分布曲线。仿真计算结果表明：“无导线，有杆塔”和“无导线，无杆塔”情况下的电位分布曲线差别不大，此时杆塔对绝缘子周围电场的影响不明显。“无导线”情况下绝缘子表面电位随着远离高压端急剧下降，前20%的泄漏距离承担了80%的电压降，靠近高压端电场分布极不均匀，靠近低压端的电位分布接近于均匀分布。当考虑导线影响时，绝缘子靠近高压端的电位分布较“无导线”情况下有所改善。“有导线，有杆塔”和“有导线，无杆塔”时相比，绝缘子靠近低压端20%泄漏距离所承担的电压降由25%降低至20%。

图6 1#有机复合绝缘子电位云图

图7 有机复合绝缘子表面电位分布曲线

通过以上分析可以得出：杆塔和导线对绝缘子周围电场有明显的影响，导线和杆塔分别对绝缘子靠近高压端和靠近低压端的电位分布起到改善作用。实际工程中可利用大截面导线或分裂导线使高压端处绝缘子承担的电压降低。

2.2 有机复合绝缘子表面电位分布

图8为2#有机复合绝缘子的电位云图，参考值为电位百分数。从绝缘子横截面的电位云图可以看出等电位线以高压端为中心，以近似圆形向周围扩散；纵切面电位云图中等电位线几乎与导线平行，绝缘子周围电场未受到截断导线末端的影响；说明导线对绝缘子周围电场分布起到了改善作用，且计算模型取导线长度20m 是满足要求的。

图9所示为两种有机复合绝缘子表面沿泄漏路径的电位分布曲线。由于采用相同的杆塔模型，清洁干燥状态下两种绝缘子的电位分布曲线在靠近低压端处几乎重合；在靠近高压端略有不同。绝缘子前20%的泄漏距离承担了约40%的电压降。

图8 2#有机复合绝缘子电位云图

图9 有机复合绝缘子表面电位分布曲线

2.3 有机复合绝缘子表面电场强度分布

图10（a）、（b）为1#和2#有机复合绝缘子电场强度云图。由图可以看出均压环与绝缘子高压端金具表面具有很高的电场强度值；由于绝缘介质与空气的介电常数差异较大，空气中的电场强度高于介质中的电场强度。

图10 有机复合绝缘子电场强度云图

图11所示为有机复合绝缘子表面电场强度分布曲线，纵轴为表面电场强度与平均电场强度的比值，平均电场强度可用绝缘子两端承担的电压除以绝缘高度求出。1#绝缘子表面最大电场强度为8.96倍的平均电场强度，2#绝缘子最大电场强度为8.63倍的平均电场强度。330kV 输电线路最高运行线电压为363kV，绝缘子两端最高承受电压为296.4kV，考虑到1#、2#有机绝缘子绝缘高度分别为2.8m 与3.3m，则1#与2#复合绝缘子在正常运行情况下其表面最大电场强度分别为9.57kV/cm 与7.82kV/cm。

图11 有机复合绝缘子表面电场强度分布曲线

3 表面电场优化

在长期电应力作用下，有机复合绝缘子表面有机材料会出现电化学腐蚀，局部电场强度高的区域腐蚀劣化更严重如图12所示。为提高绝缘子的运行可靠性，必须限制其表面的最大电场强度，使场强分布趋于均匀。

图12 有机复合绝缘子表面的电化学腐蚀

由于有机复合绝缘子表面的最大电场强度出现在靠近高压金具处，因此通过改变绝缘子高压端均压环结构尺寸可以对优化电场分布。调整图3中均压环环径、管径、罩入深度，使绝缘子表面最大电场强度值降至最小，同时依据规程要求对均压环表面的电场强度限定在20kV/cm 以内。

图13、图14分别为两种有机复合绝缘子及其均压环的表面最大电场强度随均压环管径r的变化曲线，此时均压环环径D、罩入深度H均为原始参数不变。可以看出均压环管径r对绝缘子表面电场强度的影响非常有限，随着r的增大，均压环表面最大场强明显降低。当管径r为40mm 时，均压环表面最大电场强度小于20kV/cm。

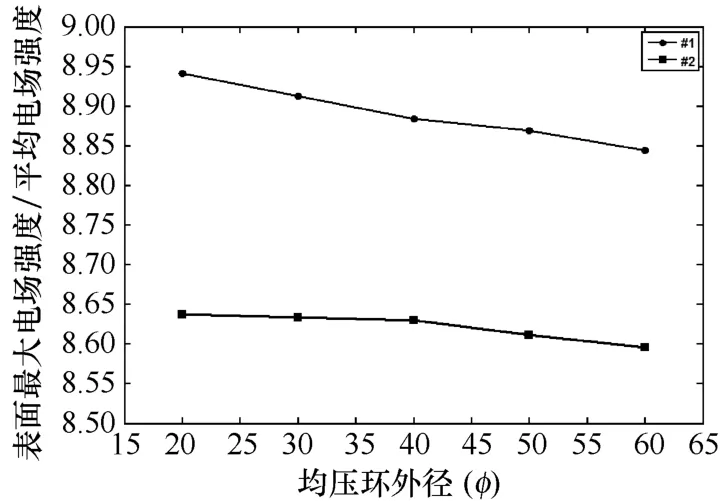
图13 绝缘子表面最大电场强度随均压环管径变化曲线

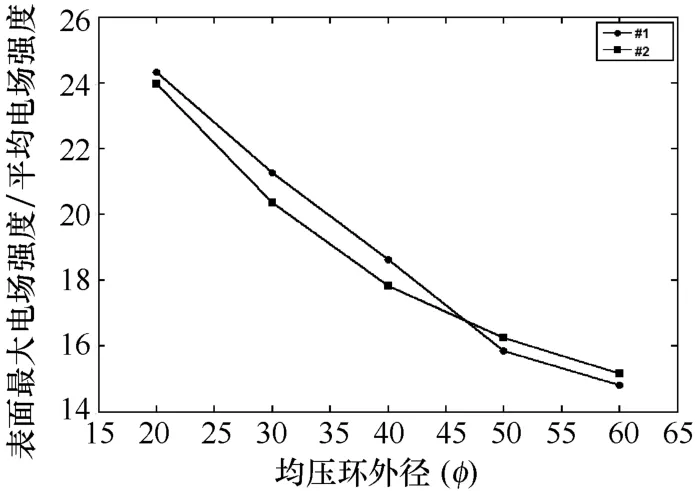
图14 均压环表面最大电场强度随均压环管径变化曲线

图15为均压环管径为40mm 时绝缘子表面电场强度最大值与均压环环径D和罩入深度H之间的关系。由图可知环径D与罩入深度H对绝缘子表面电场强度的影响不是独立的，曲面最低点所对应的坐标即电场优化后的均压环参数，详细说明可见表2。

图15 表面场强最大值与环径及罩入深度的关系

表2 有机复合绝缘子均压环参数及相关的 电场强度值/峰值

4 结论

本文基于静电场理论，采用有限元数值计算方法，建立了330kV 有机复合绝缘子的有限元模型。通过计算杆塔及导线对绝缘子周围电场的影响、绝缘子表面电场分布和绝缘子表面电场强度分布，提出了330kV 有机复合绝缘子表面电场优化的措施。通过改变绝缘子高压端均压环结构尺寸可以对优化电场分布。通过调整均压环环径、管径、罩入深度，可以使绝缘子表面最大电场强度值降至最小。同时依据规程要求对均压环表面的电场强度限定在20kV/cm 以内。由仿真可知，均压环管径r对绝缘子表面电场强度的影响有限，随着r的增大，均压环表面最大长枪明显降低，绝缘子表面电场强度最大值与均压环环径和罩入深度相关，曲面最低点所对应的坐标即为电场优化后的参数。

[1] 朱健云.基于ANSYS 盘形悬式绝缘子的模态分析[J].机械设计与制造，2012,32(12): 236-238.

[2] 关志成,王黎明,周远翔,等.复合绝缘子用于高海拔区 750kV 线路的可行性[J].高电压技术,2002,28(2): 34-36.

[3] 徐志钮,律方成,刘云鹏,等.基于有限元法的绝缘子污闪模型[J].高电压技术,2011,37(9): 2225-2232.

[4] 苑吉河.输电线路绝缘子(串)交流污闪特性及放电过程的研究[D].重庆: 重庆大学,2008.

[5] 高博,王清亮,周建博,等.干燥带对污秽绝缘子电场分布的影响[J].高电压技术,2009,35(10): 2421-2426.

[6] 蒋兴良,张志劲,胡建林,等.高海拔下不同伞形结构750kV 合成绝缘子短样交流污秽闪络特性及其比较[J].中国电机工程学报,2005,25(12): 159-164.

[7] Shi W D,Guan Z C,Wang L M,et al.A study on the selection of outdoor insulators used in high altitude areas[C]//2003 ANNUAL REPORT CONFERENCE ON ELECTRICAL INSULATION AND DIELECTRIC PHENOMENA,2003: 391-393.