基于分时电价的办公建筑中央空调最优起动时间计算

李 昌

（上海申瑞继保电气有限公司，上海 200233）

目前，建筑能源管理高级计量体系（Advanced Metering Infrastructure，AMI）实现对楼宇、家庭中用电设备的远程监控[1]，国外基于AMI 的空调远程负荷控制有3 种方式：中断控制、周期性暂停和温度控制[2-5]。第一种方式不考虑空调运行状态和办公舒适度，控制简单，第二、三种方式在注重节能同时可以满足办公舒适度的要求，具有较好的发展前景。针对我国中央空调具体情况，国家电网公司已第二种控制方式列入“十二五”营销规划。本文针对办公建筑探讨中央空调的最优起动时间问题。

需求侧管理（Demand Side Management，DSM）的目标之一是控制电网最大负荷的增长速度，减少新增装机容量，维持电力供需平衡。基本措施是减少用户在电网高峰时段电力需量，而峰谷平分时电价是实施需求侧管理的重要手段，通过价格杠杆来调节供求矛盾，从而实现电网调峰和减少用户费用支出的目的。办公建筑用能主要集中在照明、空调、动力分项上，负荷用电具有明显的时间特征。空调用电和气象数据、空调面积紧密相关，具有可控、可预测的特点，调节办公建筑的空调负荷可以较好响应需求侧管理目标。

国外文献多以空调制冷机在各时段起/停状态为决策变量，目标函数包括最小化系统峰负荷[6-7]、最小化系统运行成本[8]、以减少对空调制冷机使用寿命影响出发，加入多次起停控制约束条件。这些方法都需要中央空调能够适应远程控制体系和计量体系，对某些空调需要进行改造才能满足要求。

根据统计[9]，办公建筑总能耗中电耗比例为96%，其中空调能耗比例为40%左右，单位面积耗能平均值为114.0kWh/m2a。开展空调的最优起动时间研究：对电力企业而言，不仅减少用电需量，起到削峰填谷作用，还可以减少输配电设备备用容量[10]；采用分时电价计价策略，如果电力用户多用谷电价，还可以节省用户购电成本，减少企业开支。

以制冷为例，中央空调能耗主要能耗包括制冷机组、冷冻和冷却一次、二次水泵，风机末端用电。起动过程中，制冷机组和各种水泵负载率较高，当温度满足用户要求后，制冷机组负载率将下降，部分水泵可以优化组合，甚至退出运行。起动过程中，电能消耗将由高到低，到恒温阶段，用电负荷在一定范围内几乎保持恒定，此时空调用电负荷主要用于保持水泵运转和建筑的冷量流失。

为保证用能需求，办公建筑通常需要提前开起空调，提前开起空调时间过长，有利于利用分时电价和削峰填谷，但会导致建筑能量流失的时间变长，不利于节能，也不利于空调经济运行；提前开起的时间过短，不能满足建筑办公需求，也不利于充分响应分时电价和削峰填谷的杠杆作用。本文探讨合理控制空调的开起时间，既可以利用分时电价、削峰填谷，也能节约能源，减少企业费用支出，达到经济运行目的。

1 空调经济运行建模

根据空调用电负荷特点，把空调负荷分解为起动过程阶段、恒温阶段两个阶段。对办公建筑来说，起动过程阶段负荷大，变化小；恒温阶段负荷相对较小，负荷大小与天气情况、人口密度、空调面积保温层变化都有关，负荷仍然有变化。

1.1 空调用电负荷结构模型建立

一定时间段[t0，tn]的空调用电负荷结构如下：

式中，Ws(t0,tn)为第一阶段起动过程能耗，Wk(t0,tn)为第二阶段恒温能耗，W(t0,tn)为总能耗。Ps(t)、Pk(t)分别为起动过程能耗、恒温能耗的有功值，为时间函数。

对时间段[t0,tn]，按照分时电价时间设定，可以划分为峰谷平三段，有

式中，Th、Tl、Tm分别为峰、谷、平时间。

设第一阶段对应峰、谷、平时间为Tsh、Tsl、Tsm，第二阶段对应峰、谷、平时间为Tkh、Tkl、Tkm。则有

1.2 空调起动过程能耗模型建立

采用统计方法，选择历史日期空调起动能耗和温度曲线，建立空调起动过程用电线性模型。曲线纵坐标为能耗和温度，横坐标为时间，负荷和温度为15min 一个数据，温度为建筑室内空调平均温度。

定义规则如下。

规则1：选取时间段[Tb，Te]，该时间段为空调开起过程期间，并且温度曲线上任意一点的斜率K呈单调变化，如果制冷，斜率K＜0；如果制热，K＞0。

规则2：该时间段[Tb,Te]，满足Te-Tb＞Tset,此时间段任意一点空调负载率R大于ks。

规则3：Wb与室外温度差不大于指定温度值Wdiffmin，We与室外温差大于指定温度值Wdiffmax，并且We达到建筑管理规定的空调温度范围。

式中，Tb为时间段开始时间，Te为时间段结束时间，Te-Tb为时间长度，Tset为历史上中央空调起动阶段时长均值，根据空调起动温度曲线设定，可采用不精确的数值，从30～120min 不等，单位为（min）。dW/dt为[Tb，Te]的温度变化值，Wb为Tb时间的温度，We为Te时间的温度，Wep、Wbp分别为时间Te、Tb的室外环境温度，单位为摄氏度。P为时间Te到Tb的空调用电负荷，Pn为空调系统额定功率，单位都为kW，R为空调负载率，Wmax、Wmin为办公建筑规定的办公环境温度上下限值，ks为历史上中央空调起动阶段负载率均值，参考值0.9～1.0。

根据历史数据，找到同时满足上述3 个规则的曲线，对负荷用电进行线性化处理，计算第一阶段的平均用电负荷：

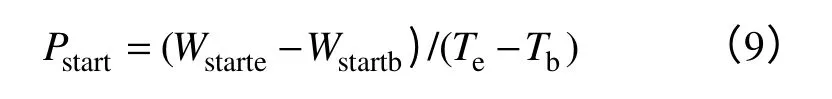
计算第一阶段的平均用电时间：

式中，Pstart、Wstarte、Wstartb分别为时间段[Tb，Te]的用电负荷线性均值、Te和Tb时间的计量表计电度数值，Tstart为第一阶段起动过程时间长度值。根据多个历史曲线，由式（9）、式（10）计算出用电负荷及用电时间，取平均值得到第一阶段平均用电负荷及平均用电时间。

1.3 空调恒温模型建立

选择历史日期空调恒温能耗和温度曲线，建立空调恒温用电线性模型。

定义规则如下。

规则1：选取时间段[Tb，Te]，该时间段为空调恒温期间，温度曲线上任意一点的斜率K在[-1/15，1/15]之间，K的定义见式（6）。

规则2：该时间段[Tb，Te]，满足Te-Tb＞Thold,此时间段空调任意一点用电负荷P与空调运行最小功率Pmin满足：

规则3：We与Wb温度差不大于指定温度Wdiffmin，并且We、Wb都达到建筑管理规定的空调温度范围。

根据历史负荷和温度曲线，找到满足上述3 个规则的曲线，对负荷用电进行线性化处理，计算第二阶段的平均用电负荷：

式中，Ploss、Wlosse、Wlossb分别为时间段[Tb，Te]的用电负荷线性均值、Te和Tb时间的计量表计电度数值，Tloss为第二阶段恒温时间长度线性均值，Thold为中央空调恒温阶段时长，可取值120～180min，kn为历史上中央空调恒温阶段负载率均值，参考值0.3～0.4。

根据多个历史曲线，由式（13）计算出用电负荷，取平均值得到第二阶段平均用电负荷。

1.4 空调经济运行目标函数

用户费用主要包括电度费用和需量费用，本文选取用户电度费用F(t,Tq) 作为目标函数，Tq为用户指定的中央空调温度达到需求温度的时间点，t为中央空调起动时间点，如下：

式中，Tstart、Ts_a、Ts_b、Ts_c分别为第一阶段空调起动总时长、峰电价时长、谷电价时长、平电价时长，Tloss、Tl_a、Tl_b、Tl_c分别为第二阶段空调恒温总时长、峰电价时长、谷电价时长、平电价时长，Mon_a、Mon_b、Mon_c分别为峰、谷和平时段电价。

设t寻优范围[t0，tn]，根据实际情况可知，最大点tn为Tq，此时t0最大值为Tq-Tstart，表示空调第一阶段完成时间在期望点Tq或者之前；t0最小值为距Tq前最近的谷时段结束时，再往前Tstart时长的时间点。

2 算例分析

算例选取上海虹桥枢纽某商务小区中央空调用电数据。

该小区由4 台离心式冷水机组，每台机组制冷量7034kW，额定功率1350kW，一次水泵200kW，二次水泵总功率150kW，总功率冷水机组集中供冷，用户建筑管理规定的空调温度范围Wmin=25，Wmax=27，Wdiffmin=0.4，Wdiffmax=5，ks=0.9，kn=0.4，Tset=75，Thold=120，指定期望温度的时间Tq为早上9 点。

峰谷平电价分别为：1.13、0.71、0.28 元/kW· h，当地：峰段：8—11、13—15、18—21 时；平段：6—8、11—13、15—18、21—22 时，谷段：22—次日6 时，如图1所示。

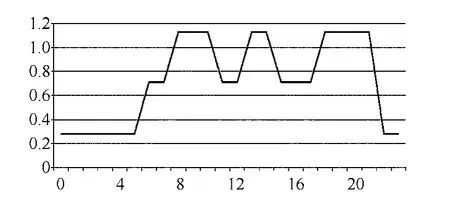
图1 24 小时分时电价图

2.1 模型初始化

选择历史同月满足1.3 节规则曲线数据，以单台空调起动过程的15min 间隔用电负荷和温度绘制曲线，如图2所示某日3∶00—13∶00 的负荷及温度曲线。

图2 负荷及温度曲线图

从图2可以看出0∶00—7∶00 待机能耗大约为140kW，起动过程在7∶15 开始，平均温度为30.9℃，到9∶00 点结束，平均温度为26.5℃。

采用多组曲线，可计算出第一阶段平均用电负荷Pstart=1265kW 及平均用电时间Tstart=105min。

选择历史同月满足1.4 节规则，以单台空调恒温过程的15min 间隔用电负荷和温度绘制曲线，如图2所示某日10∶00—13∶00 的负荷及温度曲线。从图中可以看出恒温过程在10∶00 点开始，温度为26.1℃，截止到13:00 点，温度为26.2℃，温度变化小于Wdiffmin，持续3h。

类似采用多组曲线，可计算出第二阶段平均用电负荷Ploss=507kW。

2.2 目标函数求解

采用迭代法求解，由式（14），需要求解目标函数F(t,Tq)的空调起动时间点t，使得目标函数最小。算例中的Tq=9 点，为方便计算，转换Tq、t为距离0 点的时长，则Tq=9×60min，该地区9 点前谷时间为0～6 点，6～9 点有180min 时长，t的寻优范围为[Tq-180-Tstart，Tq]。

初始值如下：

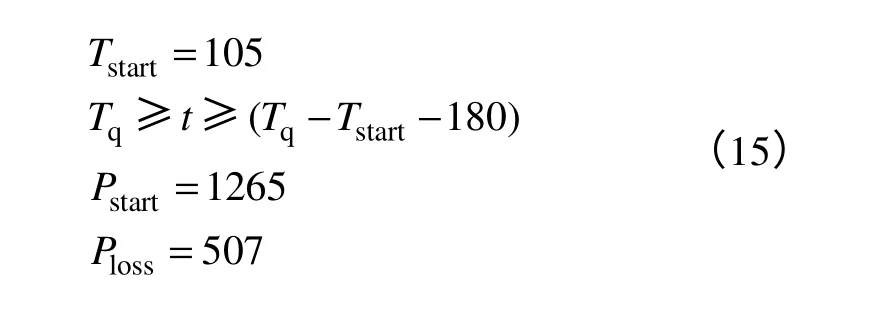
取步长nStep 为15min，对起动时间t迭代求解：

迭代计数器i从0 开始，此时t对应时间为7∶15，根据当地的峰谷平时间段，可求解出Ts_a、Ts_b、Ts_c、Tl_a、Tl_b、Tl_c，见表1。

表1 迭代中的二阶段峰谷平时长/分

2.3 最优目标函数值

对应不同的起动时间t，计算目标函数如图3所示，可以看出在4∶15 时起动空调目标函数最小，此时起动时间完全放在谷时间段，平时间段和峰时间段用来维持建筑给定温度，空调的峰时段在4∶15—6∶00，实现了空调削峰填谷的目的，减少了需量费用，此时空调运行成本最经济。当起动时间持续小于4∶15 时，增加了空调恒温时间，目标函数增大，成本增加。

图3 不同的起动时间对应的目标函数值

3 经济运行与节能分析

3.1 经济效益分析

从4∶15—9∶00 这个运行时间区间进行分析，这种方式可以在电度费用和需量费用两方面减少用户用电成本。表2分别为4∶15、7∶15 分起动，在4∶15—9∶00 时间段内空调用电成本对比。

表2 两种起动方式运行成本对比

由表2可以看出4∶15 起动，经济效益明显，可以降低需量费用60%，减少费用：30699 元，每天还可以降低电费用约88 元，具有显著经济效益，总费用降低42%。

3.2 节能分析

表3给出4∶15、7∶15 起动空调用电度数对比，可以看出采用这种方式，虽然经济性目的达到了，但用电度数增加，环保成本增加，并没有达到节能的目的。

表3 两种起动方式运行用电对比

对比两种起动方式，4∶15 起动由于要维持较长时间（3h）的空调恒温，故用电量增加，7∶15起动方式，无需提前开机，没有维持恒温的时间，故用电量少。

因此，如果加入环保成本，则表2的经济效益将减少，但从用户角度采用4∶15 起动方式具有较强的可行性，在DSM 中，是一种较好的管理方法。

3.3 起动时间点范围分析

限制起动时间点在区间[Tq-180-Tstart，Tq]，如果起动时间t小于Tq-180-Tstart，由于起动阶段的重负荷已经在谷时段，此时电度费用并不会减少，反而会增加恒温时间段，对电度费用没有任何贡献。

3.4 周期性暂停模式

在中央空调周期性暂停的成本较高，或者中央空调不能实现周期性暂停运行模式，采用本文给出的方法具有较大优势；如果中央空调允许周期性暂停模式，本文给出方法可以在恒温阶段暂停一段时间，则两阶段方法优化空间会进一步增大，此种方式兼顾了节能与经济性。

4 结论

本文提出办公建筑空调最优起动时间计算方法，根据空调负荷特性，建立两阶段模型，分别计算起动负荷和恒温负荷，以此为常数，基于分时电价建立最小成本的经济运行模型，对空调起动时间进行寻优。最后以上海虹桥枢纽商务区空调运行数据为例，计算结果表明，该方法具备较好的经济性，可以降低企业成本，计算出的空调起动时间对空调的运行安排具有重要的现实意义。

[1] 辛洁晴,吴亮.商务楼中央空调周期性暂停分档控制策略[J].电力系统自动化,2013,37(5): 49-54.

[2] 张钦,王锡凡,别朝红,等.电力市场下直接负荷控制决策模型[J].电力系统自动化,2010,34(9): 23-28.

[3] 张钦,王锡凡,付敏,等.需求响应视角下的智能电网[J].电力系统自动化,2009,33(17): 49-55.

[4] 王蓓蓓,李扬,高赐威.智能电网框架下的需求侧管理展望与思考[J].电力系统自动化,2009,33(20): 17-22.

[5] 张钦,王锡凡,王建学,等.电力市场下需求响应研究综述[J].电力系统自动化,2008,32(3): 97-106.

[6] Kurucz C N.A linear programming model for reducing system peak through customer load control programs[J].IEEE Trans on Power Systems,199611(4): 1817-1824.

[7] Chen J m.Scheduling of directload controlto minimizeload reduction for a utility suffering from Generation shortage[J].IEEE Trans on Power Systems,1993,8(4): 1525-1530.

[8] Chen J m.Scheduling direct load control to minimize system operation cost[J].IEEE Trans on Power Systems,1995,10(4): 1994-2001.

[9] 徐强,庄智,朱伟峰,等.上海市大型公共建筑能耗统计分析[C].城市发展研究——第7 届国际绿色建筑与建筑节能大会论文集,2011.

[10] 沈南飞.需量控制在电力经济运行中的应用[J].电力需求侧管理,2003(6): 41-43.