减速机二级行星轮系的动力学特性研究
2015-05-27黄继雄李清清余本钢
黄继雄,尹 敏,刘 虎,李清清,余本钢
(武汉理工大学 机电工程学院,湖北 武汉430070)
EBZ132 型掘进机[1]是用于开凿平直地下巷道的机器,主要由行走机构、工作机构、装运机构和转载机构组成。随着行走机构向前推进,工作机构中的切割头不断破碎岩石,并将碎岩运走。其截割部的行星齿轮减速机作为一种典型的减速设备,具有结构紧凑、整体尺寸小、传动比大和可靠性好等优点,被广泛地应用于起重、挖掘、运输和建筑等行业。但是,该减速机存在齿轮轮齿疲劳断裂、齿面磨损,以及振动和噪声过大的问题,因此,要提高齿轮的承载能力和传动的平稳性,降低齿轮传动的噪声,需要先对该减速机的二级行星齿轮传动系统进行动力学特性的研究,为结构优化设计提供可靠的基础。
1 减速机行星齿轮系统的基本结构
某减速机的第一级减速装置由3 个行星轮、1个太阳轮、1 个内齿圈和1 个行星架组成,其中,太阳轮、行星轮和内齿圈都是变位齿轮。与一级减速机构类似,第二级减速装置由5 个行星轮、1个太阳轮、1 个内齿圈和1 个行星架组成,其中,内齿圈与第一级共用。一级行星架与二级太阳轮固连在一起,因此具有相同的转速[2]。其二级行星减速机结构简图和相关齿轮参数分别如图1 和表1 所示。
该行星减速机的各级传动比为:
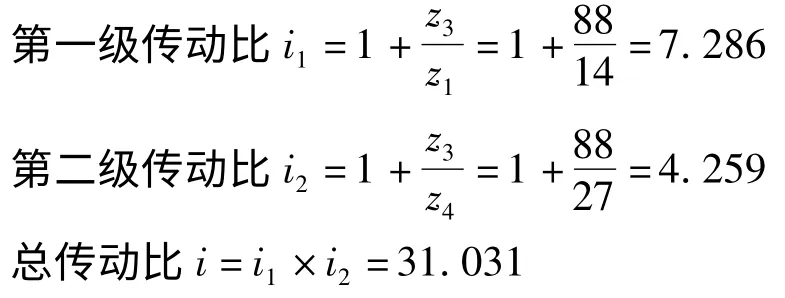
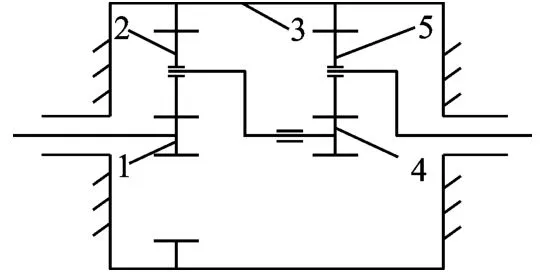
图1 二级行星减速机结构简图

表1 二级行星减速机各齿轮参数表
2 减速机动力学参数的理论计算
2.1 各齿轮转矩和啮合力的计算
该减速机的驱动电机选用抚顺电机厂生产的YBUD-132/75 -4/8 型号电机。其主要参数[3]如表2 所示。

表2 驱动电机的主要参数
根据该减速机中各齿轮的尺寸和强度条件,该电机在额定功率为132 kW,转速为732 r/min 的工况下工作。根据电机相关参数和理论,可算出减速机输出端可承受的最大负载扭矩为54 591 N·m。
运用机械动力学理论,可以计算出减速机正常工作时各齿轮所承受的转矩和齿轮间啮合力的大小。由T1=9 550P/n1(式中T1为输入转矩,P为电机额定功率,n1为输入转速)可计算出输入轴所承受的最大转矩[4]。因此,一级太阳轮的转矩为:

一级行星轮的转矩为:
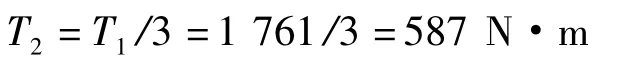
根据齿轮所承受切向力的计算公式:Ft=2 000T/d(式中d为小齿轮分度圆直径,mm),可得一级太阳轮对行星轮的切向力内齿圈对一级行星轮的切向力Ft2=Ft1。
同理,二级太阳轮所承受的转矩T3=T1×i1=12 830 N·m,二级太阳轮对行星轮的切向力Ft3=38 014 N,内齿圈对二级行星轮的切向力Ft4=Ft3。
2.2 各齿轮啮合频率的计算
通过各齿轮的转速和齿数可以计算出减速机中各对齿轮的啮合频率,将其与仿真的啮合力频域图对比分析,可以发现齿轮啮合的相关规律。
太阳轮与行星轮啮合频率的计算公式为:
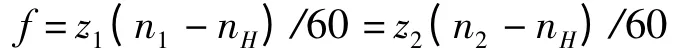
行星轮与内齿圈啮合频率的计算公式为:
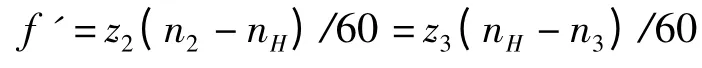
由此可知两对相互啮合的齿轮啮合频率值相等。由行星轮系公式z3/z1=i1H-1 可知一级行星架转速为nH1=n1/i1H=n1/(z3/z1+1)=100.47 r/min。同理,二级行星架转速nH2=23.58 r/min。
一级机构各对齿轮的啮合频率为:
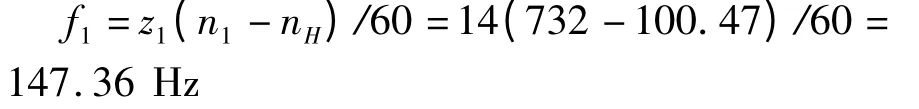
二级机构各对齿轮的啮合频率[5]为:

3 减速机的虚拟样机动力学仿真
3.1 约束和载荷的施加
基于ADAMS 对行星齿轮系统动力学仿真,施加约束是非常重要的环节,也是仿真分析结果真实可靠的重要保证。分析二级行星齿轮的运动特点后,施加的约束为:输入轴与输出轴均施加旋转副;在一级行星轮和二级行星轮上施加旋转副;在内齿圈上施加固定约束;在太阳轮与行星轮和行星轮与内齿圈之间施加接触副。该行星齿轮减速机中齿轮材料选用的是20CrMo,在施加接触副时,由于齿轮在啮合过程中具有连续接触的特点,故采用冲击函数法计算各齿轮的啮合力。根据齿轮材料和结构等查阅机械设计手册,计算出以下相关参数[6-7]:一级太阳轮与一级行星轮的接触刚度K1为7.76×105N/mm2;一级行星轮与内齿圈的接触刚度K2为11.9×105N/mm2;二级太阳轮与二级行星轮的接触刚度K3为9.24×105N/mm2;二级行星轮与内齿圈的接触刚度K4为11.2×105N/mm2;碰撞力非线性指数e取0.5;阻尼系数C为7 760 N/(s·mm);切入深度d为0.1 mm;静摩擦系数μs为0.08;动摩擦系数μd为0.05;静滑移速度υs为0.1 mm/s;动滑移速度υd为1 mm/s。
在输入轴齿轮旋转副上添加旋转驱动MOTION1,在输出轴旋转副上添加负载扭矩。设置仿真时间为1 s,仿真步数为4 000,然后求解。施加约束、驱动和载荷后的虚拟样机模型[8]如图2 所示。
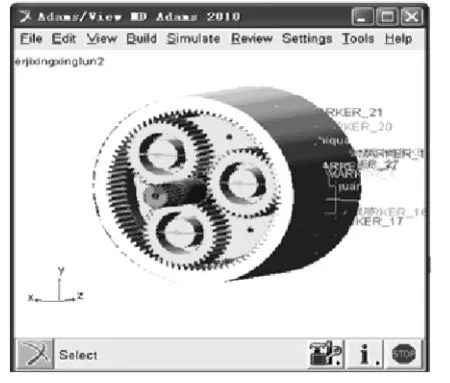
图2 二级行星齿轮虚拟样机模型界面图
3.2 仿真结果分析
对仿真结果进行处理后,可以得到各齿轮间啮合力的时域图,再对时域图进行傅里叶变换可得到啮合力的频域图[9]。从时域图和频域图中可观察到轮齿啮合力变化的相关规律。太阳轮与行星轮之间啮合力的时域图和频域图如图3 ~图6 所示。
从图3 和图5 可以看出,各对齿轮间的啮合力在稳定以后呈现周期性波动的状态,波动的周期和幅值是一个稳定的值,体现了齿轮周期性啮合的特点[10]。一级太阳轮与行星轮之间的啮合力是以16 000 N 为基准,周期性上下波动,啮合力在波动的过程中达到的最大值为22 600 N。二级太阳轮与行星轮之间的啮合力均值为37 512 N,啮合力最大值为38 595 N;对比理论计算的结果可以看出:各对齿轮间啮合力的均值都与理论计算值相吻合,仿真结果较好。从频域图中可以看出啮合力呈周期性变化,周期为一个轮齿啮合所需的时间。在一级减速机构中,齿轮间啮合力出现波峰的频率值分别为151 Hz、301 Hz、446 Hz、601 Hz 和750 Hz 等,分别是齿轮啮合频率147.36 Hz 的一倍频、二倍频、三倍频、四倍频和五倍频。同理,在二级减速机构中,齿轮间啮合力出现波峰的频率值分别为34.8 Hz、69.1 Hz、103.3 Hz和137.6 Hz,分别是啮合频率34.58 的一倍频、二倍频、三倍频和四倍频。由此可知,齿轮在其啮合频率的倍频下受啮合冲击较大,容易产生很大振动和噪声。在齿轮啮合传动的过程中,这些频率成分引起的振动是不可避免的。但是,通过优化齿轮的变位系数和中心距来增加齿轮啮合的重合度,可以减小齿轮啮合过程中啮合力的波动幅值,以及提高行星轮传动的平稳性,从而可以有效减少减速机的振动和噪声。
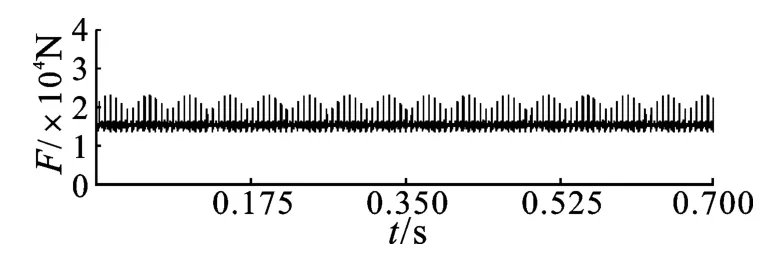
图3 一级太阳轮与行星轮啮合力的时域图
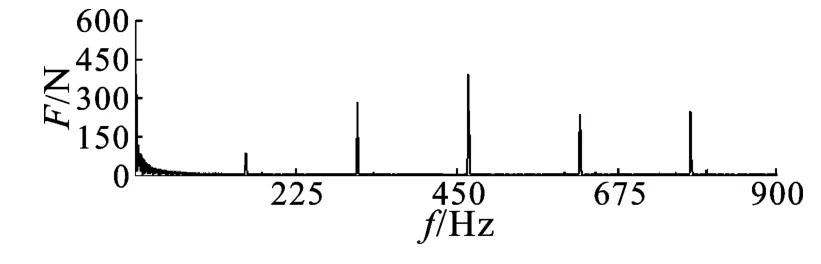
图4 一级太阳轮与行星轮啮合力的频域图

图5 二级太阳轮与行星轮啮合力的时域图
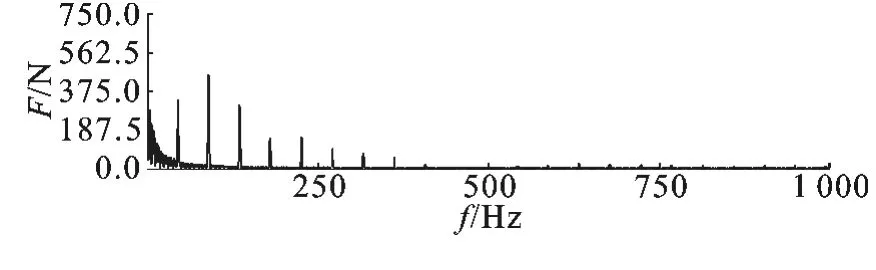
图6 二级太阳轮与行星轮啮合力的频域图
4 结论
笔者分别从动力学理论计算和虚拟样机仿真对EBZ132 型掘进机截割部减速机的行星齿轮传动系统进行了动力学特性的研究,得出了二级行星齿轮对的啮合力和啮合频率等动态特性参数,为该减速机的减振降噪及优化设计提供了基础。
[1]高承兴,刘德林. 掘进机的技术现状及发展趋势[J].煤矿机械,2009(5):3 -4.
[2]濮良贵,纪名刚.机械设计[M].8 版.北京:高等教育出版社,2006:34 -69.
[3]吴宗泽,冼建生. 机械零件设计手册[M].2 版. 北京:机械工业出版社,2013:101 -132.
[4]孙建军.悬臂式掘进机截割部减速器动态特性研究[D].长春:吉林大学图书馆,2011.
[5]朱孝录.齿轮传动设计手册[M].2 版.北京:化学工业出版社,2010:55 -102.
[6]武宝林,杨素君. 齿轮传动中啮合冲击的理论分析[J].机械科学与技术,2003(1):55 -57.
[7]龙凯,程颖. 齿轮啮合力仿真计算的参数选取研究[J].计算机仿真,2002(11):87 -91.
[8]方子帆,舒刚.齿轮传动多体接触动力学模型[J].机械传动,2009(1):15 -18.
[9]郭会珍,谭长均.基于ADAMS 的行星轮系动力学仿真[J].机械传动,2013(5):86 -89.
[10]姚娟.基于虚拟样机技术的减速器动力学仿真研究[D].武汉:武汉理工大学图书馆,2008.
