单相半桥PWM 变换器单周期控制研究
2015-05-27王友阳夏泽中
黄 刚,王友阳,徐 镭,夏泽中
(武汉理工大学 自动化学院,湖北 武汉430070)
随着对电能质量要求的提高,工业应用中对PWM(pulse width modulation)变换器的性能要求越来越高,这也促进了高功率因数变换器的研究和应用[1]。PWM 变换器具有单位功率因数能量转换的特点,其开关频率高,滤波器体积小,在中小功率场合,单相PWM 变换器的应用十分广泛。对于低输入电压和低成本应用,单相半桥PWM变换器则更有优势。
实际应用中单相半桥拓扑结构的直流侧电容桥臂上的两个电容电压存在不平衡现象,从而导致了电容桥臂中心点的电压波动。电容电压不平衡会引起交流侧电流畸变,不利于变换器系统的稳定运行[2-3]。同时,电容电压的大幅波动也降低了电容器的使用寿命。因此,单相半桥变换器控制问题,除了控制输入电流使其跟随电压达到近似单位功率因数外,还应控制电容电压的平衡。控制算法大多用于单相半桥变换器的控制[4-5],例如滞环电流控制算法和单周期控制算法。其中单周期控制算法因其简单易行而受到重视,该算法不需要采用锁相环电路,采用固定开关频率,因而不存在滞环电流控制算法因开关频率变化而带来的电磁干扰问题[6]。
笔者针对高功率因数变换器的应用需求,对单相半桥变换器进行了研究。根据单相半桥脉冲宽度调制变换器工作特点,在基本单周期控制策略的基础上对控制策略加以改进,引入桥臂电容电压反馈控制功能,以削弱桥臂电容中心点电压的波动[7]。笔者对单相半桥变换器单周期控制方法进行了理论分析和仿真,仿真结果表明了单相半桥变换器改进的单周期控制算法的有效性。
1 单相半桥变换器单周期控制基本原理
图1 为单相半桥变换器,L为储能电感;C1、C2为桥臂电容;R为负载。单周期控制采用双极性调制,根据交流侧电压极性及开关管通断状态,可以将单周期控制的单相半桥PWM 变换器分为4 种工作状态。

图1 单相半桥变换器
(1)交流电源极性为正,开关管S2导通,S1关闭,电容C2和电源串联给电感L充电。在此期间电感电流的增长斜率K1为:

式中:vs为交流电源的瞬时电压;RS为电感电流的采样比。
(2)交流电源极性为正,开关管S1导通,S2关闭,由于电感电流方向不能突变,电感电流通过S1体内二极管续流,给电容C1充电。在此期间,电感电流下降的斜率K2为:

(3)交流电源极性反向,开关管S1关断,S2导通,由于电感电流不能突变,电流通过S2的体内二极管续流,电感给电容C2充电。在此期间,电感电流下降斜率K3为:

(4)交流电源极性反向,开关管S2关断,S1导通,电容C1与电源串联给电感充电。在此期间,电感电流下降斜率K4为:

基本单周期控制算法如图2 所示,将直流母线电压V0与参考电压作比较,得到的偏差通过PI 控制器运算得到调制基准信号VM,利用一个可复位积分器可以得到一个峰峰值为2VM的锯齿波,其频率为复位时钟频率的1/2,电感电流通过采集回来后的采样电阻与三角波比较,触发RS 触发器来控制开关管的通断。
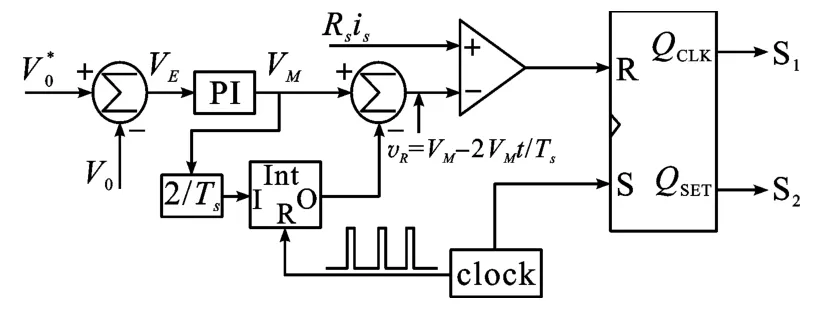
图2 基本单周期控制算法框图
根据基本单周期控制算法,经分析可画出单相半桥电感电流在一个周期内与锯齿波的变化情况,波形如图3 所示。
2 单周期控制模型分析及其改进
对基本单周期控制原理进行分析,以交流电源为正时为例,电感电流先以K1的斜率上升,然后以K2的斜率下降,通过电感电流与锯齿波比较来控制开关管的导通和截止,锯齿波斜率Km为:


图3 一个周期内电感电流与锯齿波的波形
由图3 可以得到电流关系式:

联立式(5)~式(7),可得两个开关管的导通时间t1和t2分别为:

一个开关周期近似为TS=t1+t2,从第N个周期到N+1 个周期,电感电流增加量Δis为:

根据单相半桥的拓扑结构可以看出V0=VC1+VC2,由式(11)化简得:

VC1和VC2纹波与vs同频率,忽略电压和电流高次谐波影响,与交流电源周期相比,开关周期TS很小,可以得到电流稳态向量:

由式(13)可得单周期控制的单相半桥变换器的稳态向量模型如图4 所示,将图4 中单相PWM 变换器等效成一个交流电源与电感和一个等效电阻串联,在变换器轻载工况下,等效电阻的阻抗远大于电感阻抗,电感影响可忽略[8-9],则该变换器为单位功率因数变换器,交流侧电流近似为:


图4 基于单周期的单相半桥变换器稳态向量模型
交流侧功率为:

对于图2 所示的基本单周期控制,假设变换器桥臂电容上电压相等,即VC1=VC2,则式(14)和式(15)中不含电容电压项;由于交流电源电压与电容电压波动频率相同,这样假设不影响基本单周期控制算法对电感电流的波形跟踪控制。实际上,基本单周期控制下桥臂两电容电压不相等且波动较大,使电容桥臂中心点电压波动较大,从而导致变换器系统的稳定性下降和带载能力变差等问题。针对基本单周期控制时单相半桥变换器电容桥臂中心点电压波动问题,根据上述分析,将桥臂电容的电压值引入到单周期开关反馈控制环路,可得到改进的单周期控制算法,其框图如图5所示。

图5 改进单周期控制算法框图
由图5 可知,在基本单周期控制算法的基础上,引入桥臂电容电压差值作为变量,根据式(14)可以换算到控制输入电流的变化。由单周期控制原理可知,引入桥臂电容电压差值,其作用是对检测到的电感电流对应的比较值RsIs进行补偿,该比较值的改变可改变开关管的导通时间,从而改变桥臂电容的充放电时间,很大程度上改善桥臂电容的波动情况,使电容桥臂的电压稳定在一定范围之内。

图6 基本单周期的单相半桥PWM 整理器波形

图7 基于改进单周期的单相半桥PWM 整理器波形
3 仿真实验
根据图1、图2 和图5 搭建的仿真模型,通过仿真验证了基于改进单周期的单相半桥PWM 变化器的可行性。仿真模型参数为:变换器功率为400 W;输入交流电压为90 ~110 V;C1=C2=10 000 μF;R= 400 Ω;L= 2 mH;开关频率为100 kHz。图6 为对单相半桥变换器基本单周期控制仿真波形。其中,图6(a)为基本单周期控制算法的桥臂两电容电压波形及直流母线电压波形,图6(b)为交流电压与交流电流波形(交流电压缩小到1/20)。图7 所示为对单相半桥变换器改进单周期控制仿真波形。其中,图7(a)为改进单周期控制算法的桥臂两电容电压波形及直流母线电压波形,图7(b)为交流电压与交流电流波形(交流电压缩小到1/20)。由仿真结果可知,图6所示的基本单周期控制中,交流电流信号严格跟踪交流电压信号,实现了单位功率变换,母线电压稳定在400 V,然而,电容桥臂上的两个电容电压波动较大,这意味着桥臂中心点电压不稳定,在负载或参数变化时,将影响变换器系统工作的稳定性、系统带载能力及电容的使用寿命。对基本单周期控制算法加以改进后,引入桥臂两电容电压差值变量,图7 所示的桥臂上两电容电压波动情况得到明显改善,同时实现了交流侧电流对交流电压的跟踪,实现了交流侧高功率因数。
4 结论
笔者以单相半桥PWM 变换器作为研究对象,在基本单周期控制算法基础上提出了一种改进单周期控制算法。该算法在实现变换器交流侧高功率因数的同时,通过引进桥臂电容电压差值变量,构建桥臂电容电压闭环控制,改善了基本单周期控制算法在单相半桥PWM 变换器中桥臂电容严重不平衡的问题,限制了桥臂电容中心点电压波动范围,使变换器系统稳定性和带载能力增强。仿真实验表明,改进单周期控制算法不仅能够使变换器实现高功率因数整流,还能减小桥臂电容中心点电压波动,改善整个电路性能。
[1]董翠莲,吴延华.单相半桥可逆整流电路的滞环电流控制[J].中国科技信息,2009(4):163 -164.
[2]张加胜,张磊.四象限变流器的一种统一性建模及分析方法研究[J].中国电机工程学报,2004(8):39-44.
[3]GHOSH R,NARAYANAN G.A simple analog controller for single-phase half-bridge rectifier[J].IEEE Transactions on Power Electronics,2007,22(1):186-198.
[4]JAEHONG K,HONG-SEOK S,KWANGHEE N.Asymmetric duty control of a dual - half - bridge dc/dc converter for single-phase distributed generators[J].IEEE Transactions on Power Electronics,2011,26(3):973 -982.
[5]MOSCHOPOULOS G,QIU M,PINHEIRO H,et al.PWM full - bridge converter with natural input power factor correction[J]. IEEE Transactions on Aerospace and Electronic Systems,2003,39(2):660 -674.
[6]GHODKE D V,FERNANDES B G,CHATTERJEE K.PLL less bidirectional UPF converter[C]//Proc IEEE PESC.[S.l.]:[s.n.],2006:1700 -1706.
[7]GHODKE D V,CHATTERJEE K,FERNANDES B G.Modified one cycle controlled bi - directional high power factor AC to DC converter[J]. IEEE Trans on Ind Electron,2008,55(6):2459 -2472.
[8]赵振波,许伯强,李和明.高功率因数PWM 整流器综述[J].华北电力大学学报,2002,29(4):153-158.
[9]CHONGMING Q,SMEDLEY K M.Unified constant -frequency integration control of three -phase standard bridge boost rectifier[C]//Proc IEEE Power Electron Congr,CIEP.[S.l.]:[s.n.],2000:131 -135.
