二自由度行波型超声波电机定子的优化研究

傅 平，胡锡幸，郭吉丰

(1．福州大学电气工程学院，福建福州350108;2．闽江学院物理学与电子信息工程系，福建福州350121;3．国网浙江省电力公司杭州供电公司，浙江杭州310009; 4．浙江大学电气工程学院，浙江杭州310027)

二自由度行波型超声波电机定子的优化研究

傅 平1，2，胡锡幸3，郭吉丰4

(1．福州大学电气工程学院，福建福州350108;2．闽江学院物理学与电子信息工程系，福建福州350121;3．国网浙江省电力公司杭州供电公司，浙江杭州310009; 4．浙江大学电气工程学院，浙江杭州310027)

本文从二自由度行波型超声波电机的驱动机理和基本结构出发，对定子结构进行了分析和介绍，利用所建立的有限元模型进行定子振动的模态分析。然后以电机定子表面点的振幅最大化为优化条件，对定子的结构进行优化。接着用ANSYS软件对定子进行不同倾角下的模态分析，得到定子谐振频率和倾角的关系。最后结合所设计的定子使用激光测振系统进行测试，用于确定最佳的定子倾角。测试结果表明，优化的定子使得定子表面点的振幅较大。

行波型超声波电机;二自由度;球电机;运行机理;结构设计

1 引言

多自由度超声波电机不但具有单自由度超声波电机的优点，而且还可以实现多自由度驱动。从20世纪90年代中后期开始，国内外许多研究单位对多自由度电机的研究开始转向采用超声波电机实现驱动［1］。

经近二十年的研究，已研制成若干种多自由度超声波电机。按定转子的接触方式和电机定子形状的特征，可以把多自由度超声波电机分为行波型［2］、驻波型［3］、板状［4］和柱状［5］四种，这几种球电机各有优缺点。多自由度行波型超声波电机由于制造技术比较成熟，结构简单，夹持力大，其应用前景最为看好，可用于机器人的肩腕关节、CCD云台等驱动。由文献［6］可知，若二自由度行波型超声波电机的几个定子完全相同，则在相互垂直的二个方向上力矩相等且完全解耦。

由于二自由度行波型超声波电机的输出力矩较小，我们使用了外缘倾角结构的定子［7］，可有效提高电机的输出力矩和转速。由文献［8］可知，定子表面振幅的增加可以使定子的转速增加，从而提高电机的力矩和转速。本文首先从电机的工作原理和基本结构出发，简要介绍了电机的结构，然后结合定子外缘倾角结构分析了定子的有限元模型，而后使用激光测振系统对定子进行了测试。

2 电机的驱动机理和结构

图1为二自由度行波型超声波电机的实物图。二自由度超声波电机的转子是球形［7］，若用二个定子相对驱动球形转子，球转子就能绕某一方向旋转。同样道理，与这对定子相垂直的方向也安装一对定子，就可以使球转子绕另一方向旋转。这样，通过两对定子的复合作用，可使球转子全方位转动，即具有二个自由度。

上述结构电机的基本问题是定转子结构和几何尺寸的确定，即电机结构参数的优化设计问题。

3 电机定子的设计

3.1 定子有限元模型

图2为电机所用定子的结构图，其中A为基座，B为支撑部分，C为定子弹性金属体，虚线以上部分表示定子齿，D为压电陶瓷。电机的结构尺寸和材料参数如表1所示。

图1 二自由度行波型超声波电机Fig．1 Driving principle and structure of 2 DOF USM

图2 定子结构图Fig．2 Structure diagram of stator

表1 定子结构和材料参数表Tab．1 Constructional and material parameters of stator

由Hamilton原理和压电陶瓷材料应力-应变、应变-位移及电势-电场之间的关系，可得到超声波电机定子在一个单元内的方程为:

式中，M为单元质量矩阵;C为单元阻尼矩阵;K为单元刚度矩阵;u为质点位移矢量;F为质点力矢量;v和Q分别为质点电势矢量和电荷矢量;Θ为机电耦合矩阵;P为电容矩阵。定子剖分时采用8节点六面体三维单元。

根据表1中的参数和定子尺寸，利用ANSYS软件对定子进行网格剖分，剖分后的有限元模型如图3所示。利用有限元模型，在频率0～100 kHz范围内对其模态分析，得到定子B05模态图，如图4所示。从图4中可知，B05模态的自然频率为49.3 kHz。

图3 定子剖分图Fig．3 Division figure of stator

图4 定子模态分析Fig．4 Modal analysis of stator

由文献［6］可知，电机的驱动力矩T为:

式中，φ为定子和球转子的夹角，具体分析见文献［6］;R为球转子的半径;n为定转子波峰点接触的个数;N1与N2为定子与球转子接触圆周任一接触点的法向正压力;ε为定转子的摩擦因数;ωs1、ωs2为定子表面波峰点的角速度;ω1、ω2为球转子在相互垂直的二个方向上的角速度。

若电机在制造时完全对称，则电机在二个垂直方向上的力矩相等，其中一个方向的堵转力矩T10和空载转速ω10分别为:

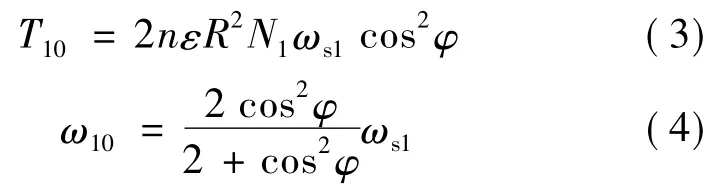
根据文献［6，7］，cosφ=r/R(r为定子有效接触半径，这里r为10mm，R为22．5mm)，由图2可知:

式中，r0为定子中线到点1的距离;L为定子弹性金属体的长度;h为定子齿的高度;β为定子的外缘倾角。

从上面的分析可以知道，当电机结构确定以后，可以微调的只有定子的外缘倾角。

3.2 定子优化设计

当定子驱动球转子时，应使定子表面质点所形成的斜椭圆和径向的夹角与φ尽可能一致，这样设计的目的是为了利用径向上的位移分量，增大定转子接触界面上的振动幅值，提高电机能量传递的效率。而定转子接触界面的能量损耗主要是由定子的径向位移造成［8］。考虑到定子结构某些参数的限制，而外缘倾角在加工后还可以做一些微调，因此把外缘倾角β作为优化设计参数。在定子外径固定的情况下，随着倾角的变化，图2所示的端点2也会随之变化。

由于电机是由多个定子驱动，而且加工误差的存在使得每个定子的频率不一定相同，通过改变外缘倾角容易使电机定子的谐振频率趋向一致［7］。综合上面的分析，径向方向上的振动幅值优化目标函数F1(L)可设为

式中，uz、ur为谐振频率下定子表面点1所在的节点在径向方向上的最大振动幅值;L为定子表面点2在x轴上的坐标值。

另外在优化设计时，希望定子在轴向方向上的振幅较大，即谐振频率下定子表面点1所在的节点的uz较大，径向方向上的振动幅值优化目标函数F2(L)可设为

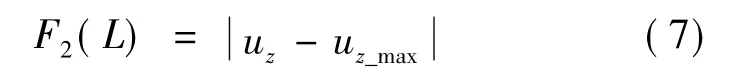
式中，uz_max是指在不同β下定子表面点1所在节点在径向方向上的最大振动幅值。

综合考虑以上两个优化目标，作相应的加权，总的目标函数F(L)为:

式中，a1、a2为相应的加权系数，这里取a1为0.65，a2为0.35。

由于定子结构的局限，设计变量限制在一定范围内，优化设计的数学模型可表述为一个有约束条件的极小化问题:

式中，L1为内径，10mm;L2为外径，15mm。

用ANSYS软件对定子进行不同倾角下的模态分析和谐响应分析，得到定子谐振频率和倾角的关系，如图5所示。从图5可知，随着倾角的增大，定子的谐振频率也增大。谐响应分析得到定子表面点1所在节点的径向振动位移、轴向振动位移随外缘倾角变化的规律，仿真结果如图6所示。

图5 谐振频率与倾角关系(仿真结果)Fig．5 Relation between β and resonant frequency (simulated results)

图6 轴向、径向振幅与倾角关系Fig．6 Relation between β and axial and radial amplitudes

4 实验结果分析

在对定子的优化设计过程中，以定子的倾角为优化设计变量，对不同倾角下定子的轴向振幅和径向振幅进行了测量。测量系统由信号发生器、功率放大器、被测物件(定子)、激光测振设备组成。信号发生器产生两路相位差为90°的正弦信号，经过功率放大器直接驱动定子使其发生振动，用激光测振设备对其表面质点的振动位移进行测量。

激光测头通过分析被测物体表面反射回来的激光，确定物体的振动速度和振动位移。我们采用德国Polytec非接触式激光测振仪，配备OFV-5000控制器。实验中，激光测振仪测量的是被测物件表面的振动速度，而需要分析的物理量是被测物件表面的振动位移。OFV-5000控制器输出的是电压信号，所以要进行振动速度-振动位移-电压信号之间的转换。

定子表面质点在轴向或径向上的振动位移x满足:

式中，x为轴向或径向上的位移;ω为激励电压角频率;ξ0为振动幅值。

质点在轴向或径向上的振动速度v为:

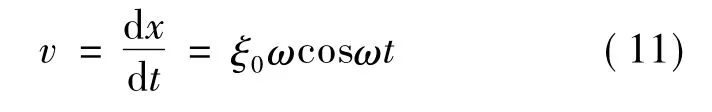
从而可以得到

式中，υmax是振动速度最大值;f是激励电压频率，且f=fs(定子的谐振频率)。

在激光测振仪中速度以电压形式表示，满足

式中，Umax是激光测振仪得到的电压信号最大值;K是电压与速度的比例系数。

如果OFV-5000控制器输出的电压信号最大值为Umax，则所测物件表面的振动幅值ξ0为:

实验时，先对不同β角下的定子进行阻抗分析，得到不同β角下定子的谐振频率fs，然后对不同β角下的定子表面点1和2进行轴向振幅和径向振幅的测量。放大器输出的激励电压峰峰值 Vpp恒为300V。

由图5可知，随着倾角的增加，定子的谐振频率fs也随着增大，由此会导致电机的工作频率与邻近模态的固有频率相近，容易产生模态混叠。模态混叠会影响定子的激励状态且会激发出噪声，所以对倾角的选取不能太大也不能太小。为了验证前面优化设计的倾角，对β∈［35°，45°］进行实验测量，共选取5个不同的倾角。图7是利用阻抗分析仪得到的谐振频率fs和倾角的关系图，其结果与图5相比略有偏差，这主要是由于图5是定子在理想状态下的谐振频率，而实际定子加工时存在加工误差以及压电片粘接时为手工操作，从而导致谐振频率理论计算值与实际值存在一定的偏差。对不同倾角下的定子表面点1和2(如图2所示)进行轴向振幅和径向振幅的测量。因为定子的半径太小，点1的径向振幅无法测量，测量了不同倾角下点2的轴向振幅和径向振幅与点1的轴向振幅，实验结果如图8和图9所示。从图8可知，β∈［35°，45°］时，点2的轴向振幅比点1的轴向振幅大。从图9可以看到，点2的轴向振幅比点2的径向振幅大，且与图6的理论计算基本一致。可以看出，随着角度的增加，其轴向振幅下降，径向振幅增加。轴向振幅下降的幅度较小，径向振幅增加的幅度较大，这有利于对径向振幅的利用。从径向振幅利用和实际加工的角度综合考虑，最后倾角取45°。

图7 谐振频率和倾角的关系(实验结果)Fig．7 Relation between β and resonant frequency (experimental results)

图8 点1、2的轴向振幅和倾角的关系Fig．8 Relation between β and axial amplitudes of point 1 and 2

图9 点2轴向振幅、径向振幅和倾角的关系Fig．9 Relation between β and axial and radial amplitudes for point 2

5 结论

在分析电机定子有限元模型的基础上，得到定子的模态方程，然后以外缘倾角为优化条件，对定子的结构进行优化设计。接着用ANSYS软件对定子进行不同倾角下的模态分析，得到定子谐振频率和倾角的关系，最后以外缘倾角为基础，计算以定子表面振幅最大化为优化条件的优化模型。

最后使用激光测振系统对定子表面质点的振动位移进行了测试，用于确定最佳的定子倾角。实验证明了该优化定子模型的有效性。

［1］郭吉丰，傅平 (Guo Jifeng，Fu Ping)．多自由度球形超声波电机的研究进展(The research progress of multidegree of freedom ultrasonic motor)［J］．电工电能新技术 (Advanced Technology of Electrical Engineering and Energy)，2005，24(2):65-68．

［2］Tomoaki Mashimo，Kosuke Awaga，Shigeki Toyama．Development of a spherical ultrasonic motor with an attitude sensing system using optical fibers［A］．IEEE International Conference on Robotics and Automation［C］．Roma，Italy，2007.4466-4471．

［3］河井元良(Motoyoshi Kawai)。超音波リニアアクチユエ一ㄆを用いた三自由度球面モ一ㄆの研究 (Research of a spherical motor with 3 DOF driven by ultrasonic linear actuators)［J］．精密工学会志 (Journal of the Japan Society for Precision Engineering)，1993，60 (3):405-410．

［4］Manaba Aoyagi，Steve P Beeby，Neil M White．A novel multi-degree-of-freedom thick-film ultrasonic motor［J］．IEEE Transactions on Ultrasonics，Ferroelectrics and Frequency Control，2002，49(2):151-158．

［5］Chen Qiang，Hu Minqiang，Jin Long，et al．Force transmission model of a cylindrical linear ultrasonic motor［A］．Proceeding of International Conference on Electrical Machines and Systems［C］．Seoul，Korea，2007.1623-1628．

［6］胡锡幸，郭吉丰(Hu Xixing，Guo Jifeng)．2自由度球形行波型超声波电动机的特性计算模型 (Mechanical characteristics calculation of 2DOF spherical travelingwave type ultrasonic motor)［J］．机械工程学报 (Journal of Mechanical Engineering)，2009，45(3):229-233．

［7］傅平，沈润杰，帅光举，等 (Fu Ping，Shen Runjie，Shuai Guanju，et al．)．二自由度行波型超声波电机的研制 (Design of spherical two-degree-of-freedom traveling-wave type ultrasonic motor)［J］．宇航学报 (Journal of Astronuatica)，2009，30(1):367-372．

［8］莫岳平(Mo Yueping)．振动模态与超声波电机性能关系的研究 (Research on relation between vibration mode and ultrasonic motor’s performance)［J］．电工技术学报 (Transactions of China Electrotechnical Society)，2002，17(3):7-11．

Optimization research of stator with two degree-of-freedom traveling-wave spherical ultrasonic motor

FU Ping1，2，HU Xi-xing3，GUO Ji-feng4
(1．College of Electrical Engineering，Fuzhou University，Fuzhou 350108，China; 2．Department of Physics and Telecommunication Engineering，Minjiang University，Fuzhou 350121，China; 3．Hangzhou Power Supply Company of State Grid Zhejiang Electric Power Company，Hangzhou 310009，China; 4．College of Electrical Engineering，Zhejiang University，Hangzhou 310027，China)

The driving principle and basic structure of this kind of spherical ultrasonic motor are firstly introduced．Then optimal structure of stator is analyzed．By the established finite element model the stator vibration modal analysis is carried out and the resonance frequency can be calculated．And then according to the optimization conditions for dip angle of stator，the structure of the stator is optimized．Through ANSYS software the modal analysis and the harmonious response analysis in different dip angles of stator can be completed．So relation between resonance frequency of stator and dip angle can be deduced．Finally test of designed stator is carried out by laser vibration test system．The best angle of the stator can be determined and the significant experimental data can also be obtained．The test results show that the optimized stator is more in line with the actual operation characteristics，which is a more accurate guide for the motor design．

traveling wave type ultrasonic motor;two degree-of-freedom;spherical motor;working principle; structural design

TM355

:A

:1003-3076(2015)05-0030-05

2014-02-17

国家自然科学基金项目(51277091)、中国博士后科学基金特别资助项目(2013T60637)、中国博士后科学基金项目(2012M521267)、福建省科技计划重点项目(2011H0017)、福建省中青年教师教育科研项目(JA14246)

傅 平(1974-)，男，福建籍，副教授，博士后，从事行波型超声波电机及其控制方面的研究;胡锡幸(1982-)，女，浙江籍，工程师，博士，从事电气试验及状态检修相关工作。