井下防爆车发动机阻尼系统缓冲解耦优化
2015-05-25陈俊海孙大刚韩斌慧宋勇王新李飞
陈俊海,孙大刚,韩斌慧,,宋勇,王新,李飞
(1.太原科技大学机械工程学院,太原030024;2.中国煤炭科工集团太原研究院有限公司,太原 030006)
井下防爆车发动机阻尼系统缓冲解耦优化
陈俊海1,孙大刚1,韩斌慧1,2,宋勇1,王新2,李飞1
(1.太原科技大学机械工程学院,太原030024;2.中国煤炭科工集团太原研究院有限公司,太原 030006)
防爆发动机剧烈的振动对车辆使用寿命影响较大,针对上述问题,以WC5E型防爆胶轮车发动机为研究对象,建立其六自由度力学模型,研究发动机各阶振动频率分布及振动耦合情况,利用Matlab优化工具箱对阻尼元件刚度参数进行优化,实现系统固有频率的合理配置和振动解耦程度的提高,最后对原车及解耦优化后车辆进行动态测试试验,结果显示优化后的阻尼系统大大的衰减了发动机振动向车架的传递,起到了良好的缓冲效果。
防爆发动机;阻尼系统;缓冲;解耦
防爆胶轮车运用于井下低矮巷道运输,防爆发动机是胶轮车的动力源同时也是振动和噪声的主要来源,井下巷道路面情况复杂,由防爆发动机产生的振动对整车使用寿命及性能发挥有很大的影响。发动机的振动往往不是单一模态振动,而是多个模态耦合振动,使得振动振幅增大。关于发动机振动解耦国内外学者做了大量的研究,提出了如弹性轴、扭矩轴及能量解耦等方法[1-5]。然而,上述研究大多针对汽车发动机阻尼系统,鲜见关于防爆工程车辆发动机振动解耦的研究。在实际运用中,防爆工程车辆发动机阻尼元件常常选取简单的减振垫来减小发动机振动向机架的传递,其隔振效果有限,因此有必要对其阻尼系统分析设计。针对上述问题,以WC5E型防爆胶轮车发动机为研究对象,从能量解耦的角度优化其阻尼元件参数,使得发动机振动各阶模态耦合情况有所改善。
1 发动机阻尼系统建模及解耦分析

图1 车辆-发动机动力学模型Fig.1 Dynamic model of vehicles-engine
防爆胶轮车可以看作是一个多自由度弹性系统,据振动理论相关知识,建立如图1所示的车辆-发动机动力学模型,模型坐标系O-XYZ原点位于车辆质心处,X轴取为车辆前进方向,为正,Z轴垂直向上,Y轴由右手定则确定;其中me、mf分别表示发动机质量和车架质量,Kg.fe、fg分别表示来自发动机和地面的激振力,N.综合车辆外形尺寸、机舱空间限制等因素影响,防爆柴油机阻尼系统采用四点平置式布置,其位置具体如图1中1、2、3、4所示。
在发动机阻尼系统隔振设计中,常常将发动机及车架视为刚体,橡胶元件忽略其扭簧作用,简化为三向刚度弹簧。综上所述,建立发动机阻尼系统力学模型如图2所示,坐标系各轴方向选取与前述一致,原点位于发动机质心处:

图2 发动机阻尼系统动力学分析模型Fig.2 Dynamic analysis model of engine damping system
对于第i个阻尼元件,其支反力FTi和反力矩Fθi分别为:

Ki为第i个阻尼元件刚度矩阵,kxi、kyi、kzi表征第i个阻尼元件三向刚度参数;Bi为位置转换矩阵,xi、yi、zi为第i个阻尼元件在质心坐标系下的位置。
将式(1)、式(2)合并可得:

利用同样的方法可以得到阻尼系统的阻尼矩阵,因此如图1所示动力学分析模型其振动微分方程为:
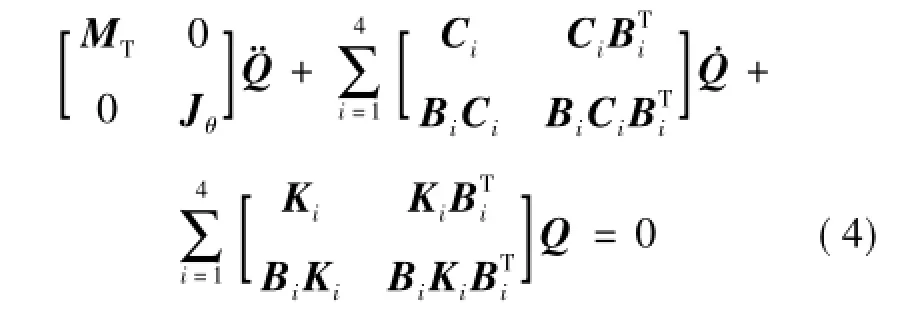
对系统自由振动分析时,可忽略橡胶阻尼对降低共振峰值的作用,系统自由振动方程可简化为:

m表示发动机质量;Iij(i,j=1,2…6)表示发动机惯性参数。
据振动理论相关知识,发动机振动可以看作是刚体作多自由度耦合振动。刚体在作某方向的振动,其振动能集中于该方向上时,这样就实现了该方向振动与其他方向振动的解耦[6]。
刚体作多自由度振动时,其系统作第j阶振动时,其最大振动能由下式表示:

第k个广义坐标分配的能量为:

综上所示:当系统以第j阶固有频率振动时,第k个广义坐标所占的能量百分比Pkj为:

式中:Φj为系统的第j阶振型;(Φj)k及(Φj)l分别为第k和第l个元素;mkl为系统质量矩阵的第k行第l列元素;k,l,j=1,2,…,6.
依据公式(8)可求出系统作多自由度振动时其振动能在各阶固有频率下的能量分布,据此分析其振动耦合情况,可以判断出系统是否存在振动耦合。系统作第j阶固有频率时,Pkj越大表示振动能主要集中于该方向,与其它方向振动耦合越低。
2 阻尼系统优化设计
2.1 约束条件
防爆胶轮车工作在煤矿井下巷道,其路面等级较低,由地面扰动引起的激励频率约为0.1~5 Hz[7].对阻尼系统设计时,发动机自身的激励相对与地面激励影响大些,因此本文重点对发动机内部激励频率进行分析。
发动机内部激振频率有燃烧激振频率和惯性力激振频率[8],其计算如下:

式中:n为发动机转速;i为发动机汽缸数;τ为发动机冲程数;Q为激励的谐次(1阶不平衡力取1,2阶不平衡力取2).
针对所使用的发动机为直列六缸四冲程发动机,怠速转速为600 r/min,各阶不平衡力相互抵消,数据代入公式(9)计算燃烧激振频率可得为30 Hz,根据隔振理论,系统的固有频率满足不大于激振频率1的关系时,才能够取得良好的隔振效果。因此在阻尼系统设计时,应将系统的固有频率比控制在21.2 Hz以下。
综上所述,阻尼系统固有频率应控制在5 Hz到21.2 Hz之间,即5 Hz≤f≤21.2 Hz.
2.2 设计变量
发动机阻尼系统设计中影响较大的因素主要有阻尼元件安装位置、角度及阻尼元件的刚度参数。在本文中车辆属于定型产品,其元件安装位置以及安装角度不便改动,且基于制作阻尼元件成本考虑,四个橡胶阻尼元件结构各向刚度参数相同,只有橡胶阻尼元件刚度参数可以改变,因此,本文选取橡胶阻尼元件的三向刚度参数(共3个,分别为kxi、kyi、kzi)作为本次优化的设计变量。
2.3 目标函数
由前文,Pkj值越大表示系统的解耦程度越高。因此阻尼系统的优化目标函数为:

综上所述:优化设计数学模型为:
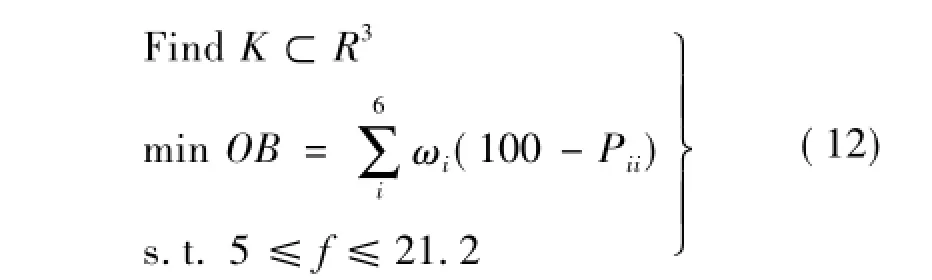
利用Matlab优化工具箱编制其计算及优化程序,算例如下:

表1 阻尼系统参数Tab.1 Damping system parameters

表2 原车阻尼系统固有频率及能量分布/%Tab.2 The natural frequency and energy distribution of original car damping system/%
防爆胶轮车发动机阻尼系统参数如表1所示,发动机质心及惯性参数由发动机生产厂家提供,通过实验的方法得到阻尼元件的三向刚度参数;由表2可以看到阻尼系统固有频率在7.6~34 Hz,各阶频率或接近发动机固有频率(约为30 Hz)或大于发动机固有频率,且从第二阶到第六阶固有频率过于接近,容易引起共振,频率配置不合理。由表2,对应发动机主要激振力方向(z和θx)其振动解耦程度只有27.9%和29.6%,与其它方向振动耦合比较严重,有必要对阻尼系统参数进行优化设计。
表3、4分别为优化后阻尼系统固有频率、能量分布及阻尼元件刚度参数。对比表2、3,优化后系统固有频率配置在6.85~21.09 Hz之间与发动机固有频率相距较远,且各阶固有频率相差大于1 Hz,不易引起共振;对于发动机主要激振力方向(z和θx)其振动解耦程度分别达到了93%和91.27%,与其他模态的振动解耦较高,并且其他方向模态振动解耦程度也达到了85%以上,优化取得了良好的效果。

表3 优化后阻尼系统固有频率及能量分布/%Tab.3 The natural frequency and energy distribution of optimized damping system/%

表4 优化后橡胶悬置元件静态刚度值/(N/mm)Tab.4 Static stiffness of optimized rubber suspension elements/(N/mm)
3 实车试验
对原车及优化后车辆,采用东华测试系统对其各橡胶元件振动前后加速度进行测量,通过减振前后加速度对比得到其振动传递率。以右前橡胶元件为例,图3、4分别为原车及优化后车辆右前橡胶元件减振前后加速度时域信号,其中右前上、下分别测量减振前、后加速度;其它各测点采用与上述一致的布置方法。对比图3、4,优化后加速度分布相对集中,其峰值也比原车有多降低。通常采用振动加速度的均方根值来作为驾驶员人体舒适性的评价指标[9],各测点振动加速度的均方根值如表5所示。由表5,优化后各元件振动传递率相较于原车有所降低,右前位置优化程度较高;优化后车辆驾驶室垂向加速度振动均方根值较原车由3.21 m/s2下降到1.14 m/s2,降低了64.3%,大大提高了驾驶员驾驶车辆的舒适性。综上所述,优化后的阻尼系统大大的衰减了发动机振动向机架的传递,起到了良好的缓冲减振效果。

图3 原车右前阻尼元件减振前后加速度Fig.3 Acceleration of original car right-front damping element before and after damping

图4 优化后右前阻尼元件减振前后加速度Fig.4 Acceleration of optimized car right-front damping element before and after damping
4 结论
(1)针对防爆胶轮车发动机振动剧烈的问题,建立其六自由度力学模型,从振动能解耦,固有频率合理配置的角度对阻尼元件参数进行了优化设计;
(2)优化后的阻尼元件,经计算和实验,其结果表明取得了良好的解耦效果和缓冲效果,有效的衰减了发动机振动向车架的传递;
(3)对胶轮车发动机阻尼系统的设计研究可以为其它工程车辆发动机阻尼缓冲提供一定的参考。
[1]梁天也,史文库,洪泽浩,等.发动机悬置系统优化设计[J].噪声与振动控制,2007,8(4):44-46.
[2]JEO-YEOL PARK,RAJENDRA SINGH.Effect of non-proportional damping on the torque roll axis decoupling of an engine mounting system[J].Journal of Sound and Vibration,2008(1):841-857.
[3]YUNHE YU,NAGI G,NAGANATHAN RAO V,et al.A literature of automotive vehicle engine mounting system[J].Mechanism and Machine Theory,2001(36):123-142.
[4]赵艳杰.基于Matlab的动力总成悬置系统参数优化设计[J].机械设计,2009,8(8):62-65.
[5]徐石安.汽车发动机弹性支承隔振的解耦方法[J].汽车工程,1995,17(4):198-204.
[6]吕兆平.能量解耦法在动力总成悬置系统优化设计中的运用[J].汽车工程,2008,30(6):523-526.
[7]江帅.煤矿井下无轨胶轮车油气悬架动态特性仿真与优化[D].太原:太原理工大学,2010.
[8]张保成,苏铁熊,张林仙.内燃机动力学[M].北京:国防工业出版社,2009.
[9]郑木莲,孟建党,张世铎,等.路桥过渡段上车内人体舒适性评价方法[J].长安大学学报:自然科学版,2012,32(2):1-6.
Decoupling Buffer Optimization of Mine Explosion-proof Car Engine Damping System
CHEN Jun-hai1,SUN Da-gang1,HAN Bin-hui1,2,SONG Yong1,WANG Xin2,LI Fei1
(1.College of Mechanical Engineering,Taiyuan University of Science and Technology,Taiyuan 030024,China;2.Tai Yuan Institute co.,LTD.of China Coal Technology and Engineering Group,Taiyuan 030006,China)
Severe engine vibration is proved to have larger impact on the life of vehicle.According to this problem,using the WC5E type explosion-proof-vehicle engine as the research object,the six degrees of freedom mechanical model was set up,and the engine's vibration frequency distribution and vibration coupling case were analyzed.Matlab optimization toolbox was applied to optimize damping element stiffness parameters so as to realize reasonable allocation of system natural frequency and improve the vibration decoupling rate.At last,dynamic testing experiment was made on both the original car and decoupling-optimized vehicle,the results show that the optimized damping system greatly reduce the vibration transmission from the engine to the frame and play a good vibration buffer effect.
explosion-proof engine,damping system,buffer,decouple
TH113.1
A
10.3969/j.issn.1673-2057.2015.03.014
1673-2057(2015)03-0228-05
2014-12-18
山西省研究生优秀创新项目(20143086);天地科技工艺技术创新基金(KJ-2013-SXMJ-05)
陈俊海(1991-),硕士研究生,主要研究方向为工程车辆振动和噪声的阻尼控制。
