花键冷敲精密成形接触面积数值计算与分析

刘志奇，卢泓昱，曲 博，王伟杰

(1.太原科技大学机械工程学院，太原 030024; 2.金属材料成形理论与技术山西省重点实验室，太原 030024)

花键冷敲精密成形接触面积数值计算与分析

刘志奇1，2，卢泓昱1，2，曲 博1，2，王伟杰1，2

(1.太原科技大学机械工程学院，太原 030024; 2.金属材料成形理论与技术山西省重点实验室，太原 030024)

通过分析冷敲精密成形的金属变形过程、加载过程和边界条件，建立花键冷敲精密成形接触面积数学模型，对接触面积进行理论计算;被成形件在滚压模具中连续快速发生局部塑性变形，为了对花键类零件冷敲精密成形工艺的机理和工艺力学进行研究，通过分析花键冷敲精密成形过程滚打轮与工件接触过程，建立工件进给量与滚打道次数值关系，得出工件进给量与各道次之间打入深度关系及各道次面积演化规律;应用MATLAB数值分析软件对接触面积影响因子进行数值计算与仿真分析。

花键;接触面积;数学模型;数值计算

冷敲成形是一种新型的近净成形技术，工件在滚打轮多次冲击载下发生塑性变形最终形成齿形，由于其变形过程复杂，为了能够更好研究花键轴变形特性情况，研究滚打轮与工件接触面积对揭示成形过程力能关系有重要意义。成形过程中，虽然加载时间短，但滚打轮与工件接触过程是一个渐变过程，该过程各阶段接触面积直接影响力能关系，进而对工件成形成性产生直接影响;而接触面积与工艺参数、滚打轮尺寸有直接数值关系，因此研究接触面积成为分析工艺条件对成形质量和精度的重要因素。

本文在剖析该工作原理基础上，建立数学几何模型，进而得出三个方向接触面积解析解，并且根据工艺参数得出各道次之间的数值关系，根据该数值关系进一步求出各道次接触面积演化过程，最终借助MATLAB数值计算软件模拟仿真不同工艺参数对接触面积的影响规律。

1 接触面积的数学模型

1.1 花键冷敲成形几何关系建立

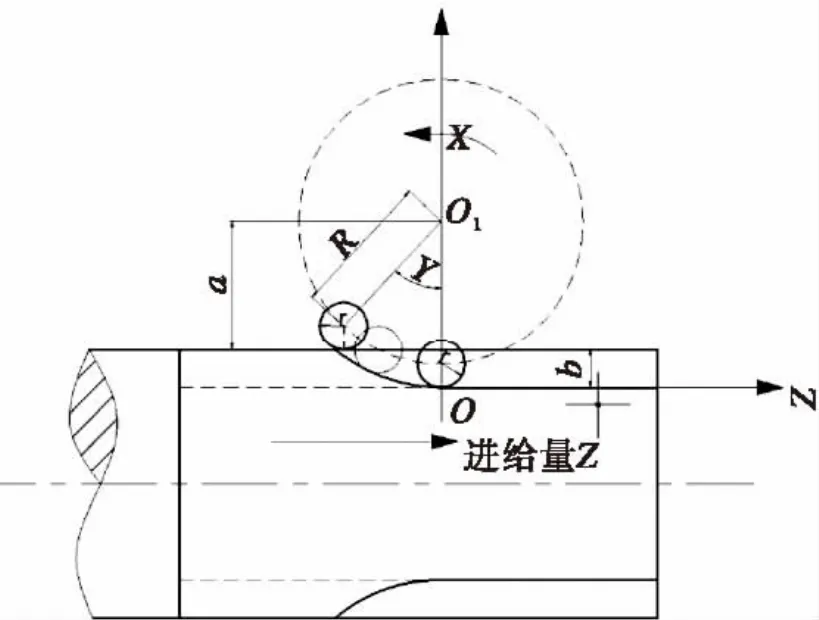
图1 花键冷敲几何关系Fig.1 Geometrical relationship of rapid cold-rolling spline

花键冷敲成形过程中，滚打轮与工件的实际接触面是一个三维曲面且随着γ角的变化而变化，为了简化计算，可将滚打轮与工件的接触区域分别向径向、轴向和切向投影，可得径向投影面积Sr，轴向投影面积Sz和切向投影面积ST.花键冷敲成形的几何模型如图1所示，取工件轴心方向为Z轴，X轴垂直于工件轴心与滚打轮轴心所确定的平面，图中R为回转半径，回转圆心为O1;r为滚打轮半径;d为滚打过程中打入量;γ为滚打轮刚刚与工件毛坯接触时与X轴的夹角;ɑ为XOZ平面内滚打轮回转中心与工件毛坯外缘的径向间距。建立接触面积数学模型前做如下假设:

(1)忽略工件、滚打轮弹性变形;

(2)工件在压缩量形成过程中滚打轮轮廓与花键成形齿廓相一致。

1.2 数学模型的建立

冷敲成形过程中，从滚打轮接触工件坯料到分离，实际接触面积是根据γ角的变化而变化的。不同位置的γ和打入量d的关系为:

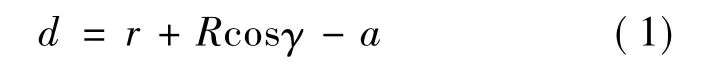
矩形花键和渐开线花键切向投影面积可以近似求取，但由于投影面积随着γ角的变化而变化。

在XOZ平面内，γ角为滚打轮过滚打轴轴心与X轴的夹角，则在一次滚打过程中，不同位置θ和打入量d的关系为:

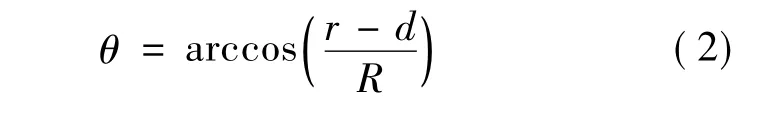
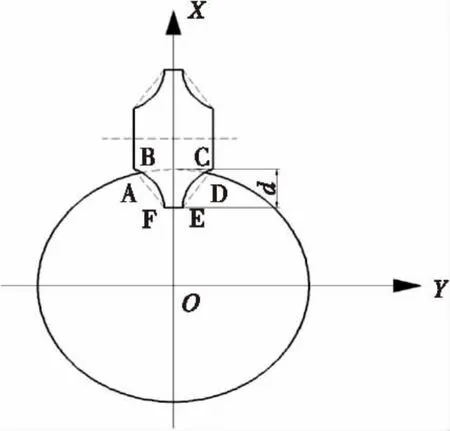
图2 滚打轮与工件接触区域切向投影面积Fig.2 Tangential projected area of contact area between die and workpiece

如图2所示，区边梯形ADEF为矩形花键;区边梯形BCEF为渐开线花键切向投影面积。由于AD或BC段是一圆心角很小的曲线段，因此近似可认为该曲线段为一直线段。这样根据梯形面积可计算梯形花键沿滚打轮切线方向与毛坯的接触面积:

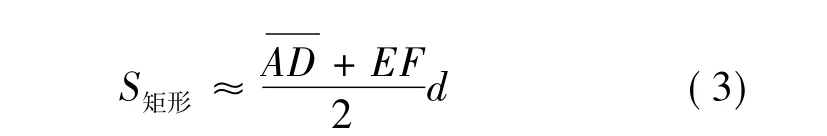
对于渐开线花键，根据齿廓方程可求出BF曲线方程，即可求出渐开线花键切向投影面积:

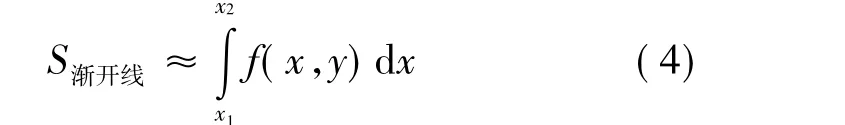
其中f(x，y)是关于渐开线齿廓的方程，我们可以根据渐开线齿廓的直角坐标方程得出齿廓上个点坐标[2]，继而对其最小二乘法[12]拟合得到齿廓曲线函数f(x，y).

(2)径向投影面积Sr:

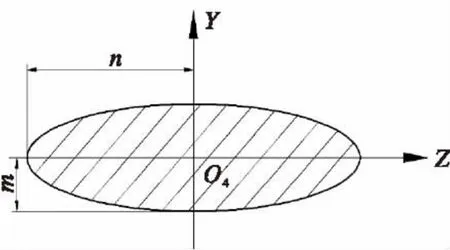
图3 滚打轮与工件接触区域径向投影面积示意图Fig.3 Radial projection area of contact area between die and workpiece

如图3所示，阴影部分面积为滚打轮与毛坯接触区域径向实际投影面积，椭圆为滚打轮与工件接触区域径向投影面积。为了便于计算，椭圆的面积近似表示径向投影面积。其中，m为椭圆长半轴，n为椭圆短半轴，由此可得径向投影面积为:

(3)轴向投影面积Sz:

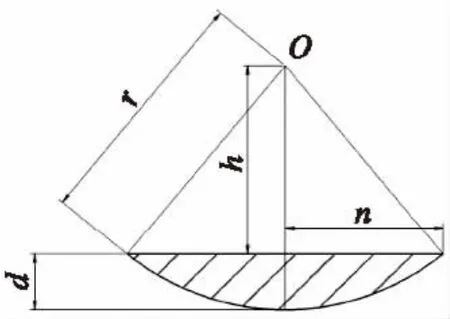
图4 滚打轮与工件接触区域轴向投影面积Fig.4 Axial projection area of contact face between die and workpiece

轴向投影面积如图所示，根据几何关系求得:

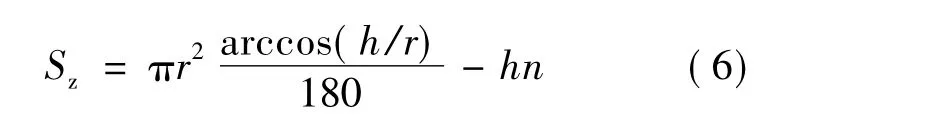
2 接触面与工艺参数关系

花键冷敲成形过程是多道次渐进成形过程，对工件一点的成形过程进行观察可知，花键齿槽齿廓成形过程属于渐进演变过程，该过程与工件进给速度有密切关系，进给量的变化直接导致花键成形道次的变化，因此研究进给量对花键成形道次影响，并建立几何模型与数学模型对指导花键冷敲成形演化规律有重要意义。

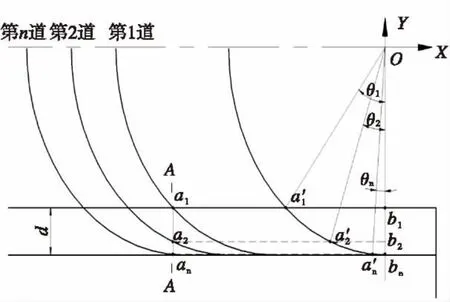
图5 建立直角坐标系下多道次成形过程Fig.5 Cartesian coordinate system of multiple passes forming process

如图5所示，对工件一点进行跟踪，从滚打轮首次接触到最后分离，工件随着进给量的轴向运动与滚打轮的打入，点由最初位置运动到点。根据公式计算得到每一进给量滚打轮的打入深度，确定跟踪点由初始位置到最终位置所需道次。

图5中圆O的方程为:

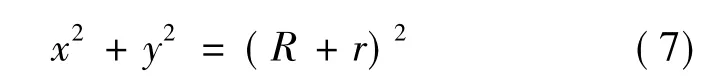
其中R为回转半径，r为滚打轮半径，d为打入深度，z为单次进给量。

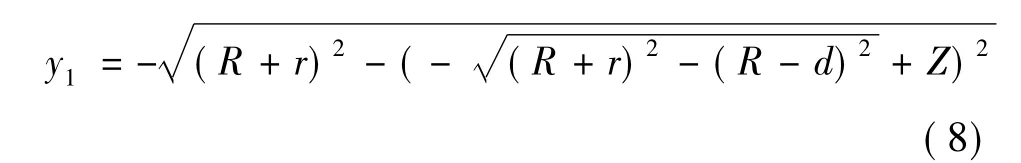
由y0、y1可以求出第一次敲击深度:

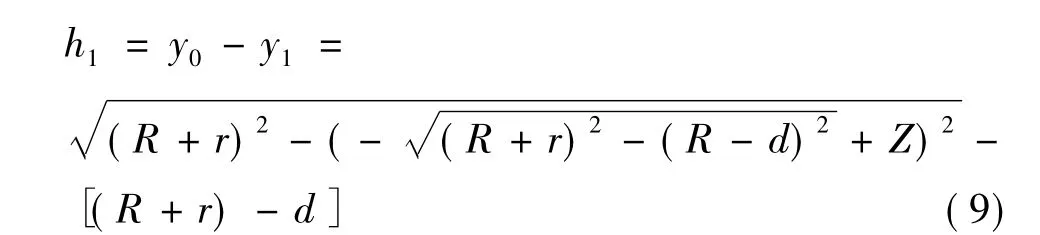
依次类推可得:

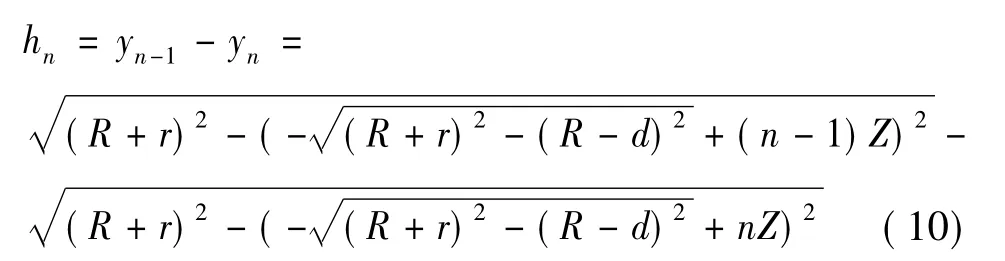
化简后得:

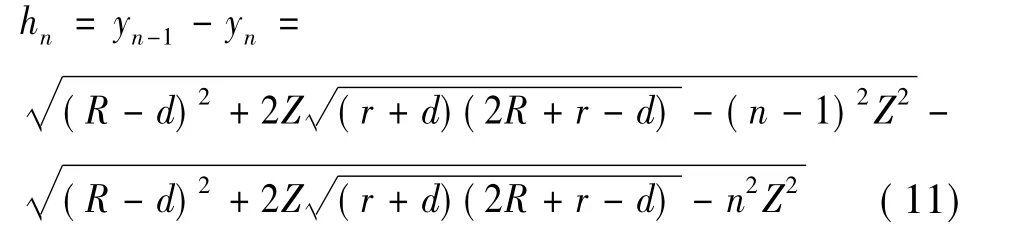
其中0＜z＜x0;n为滚打道次数，当回转半径和进给量一定时，滚打轮半径越大，滚打道次越多，成形效率越低;当r越小时，滚打道次变小，成形质量越差。为了保证加工效率，又要满足成形质量前提下，选择合适的进给量和滚打轮半径是非常重要的。

3 数值仿真分析

3.1 模数对接触面积的仿真分析

接触面积是关于m、r的函数，即S=f(m，r);但是当模数确定后，滚打轮与工件的接触面积只与r有关，为了研究接触面积关于模数的变化规律，我们采用控制变量法取r=20 mm，通过数值分析软件MATLAB对接触面积进行定量计算分析，可得如下结果:

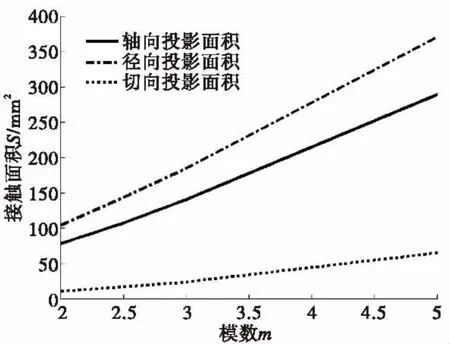
图6 模数m对接触面积S影响规律Fig.6 The impact of modulus m on contact area S

由图6可以看出随着花键模数增大接触面积也随着增大，而切向投影面积随着模数的增大变化比较缓慢，径向和轴向投影面积随着模数增大急剧增大。

3.2 各道次接触面积的仿真分析

由于花键冷敲成形是多道次渐进成形过程，工件上一横截面是由滚打轮n次敲击累积效应继而包络出齿廓形状。各道次打入工件深度受回转半径R，滚打轮尺寸r，花键模数m，进给量Z的影响，即h= h(R，r，Z，m);由于表达式变量较多，因此借助MATLAB对其进行定量计算分析。取基本参数R= 102.5 mm、r=20 mm、Z=3 mm/s、m=3;研究各道次递增切向投影接触面积δS演化规律。

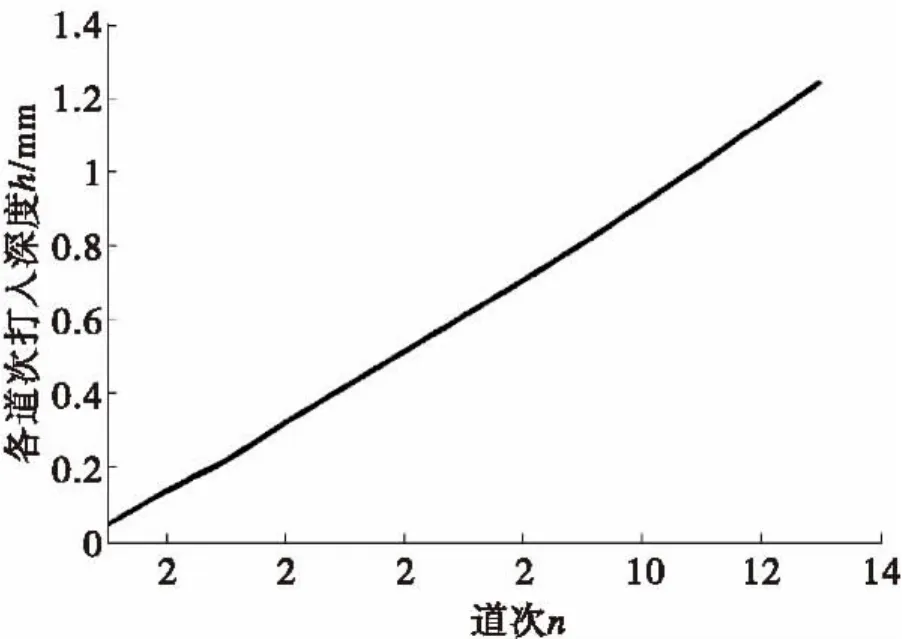
图7 道次数n与打入深度h的数值关系Fig.7 The numerical relation between n and h

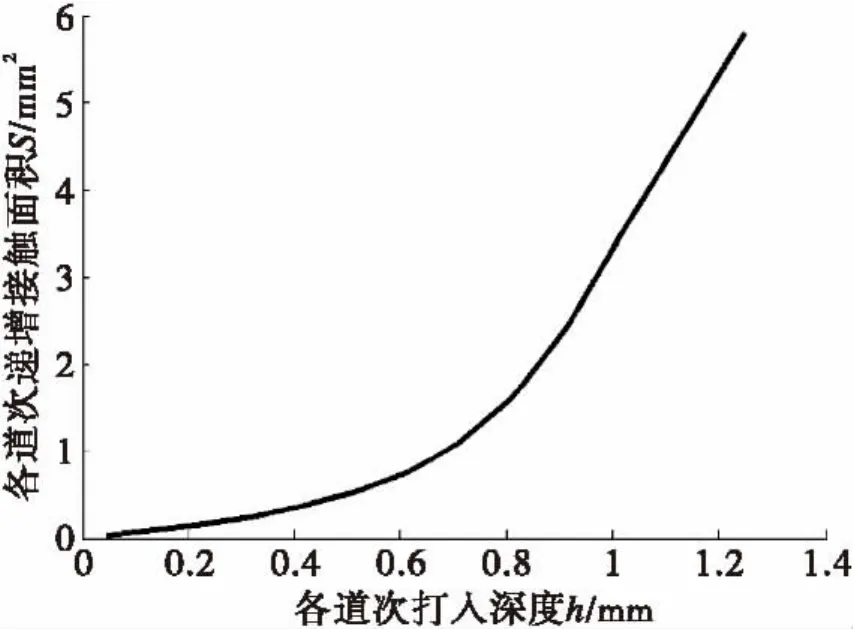
图8 打入深度h对δS的影响规律Fig.8 The impact of h on δS

图8可以看出随着滚打轮打入道次增加，各道次打入深度也在增加，且成近似线性关系;由图9可以看出h小于0.6 mm之前，曲线比较平缓，在该点之后呈指数形式增加;综合图8可以得出在前6道次内随着滚打轮打入深度增加，接触面积增加较小，随着道次增加，打入深度增加，当打入深度大于0.8 mm之后，接触面积急剧增加。

3.3 滚打轮尺寸对接触面积仿真分析

花键冷敲成形过程中滚打轮尺寸r是其接触面积影响因子之一，对于一定模数齿数的成形件来说，滚打轮尺寸对轴向和径向投影面积起主要影响作用，增大滚打轮尺寸一定程度可以提高成形效率，但滚打轮过大会使其与工件接触面积增大以致滚打轮能量耗散分散，这对成形质量产生重要影响。因此研究滚打轮尺寸对接触面积影响规律。

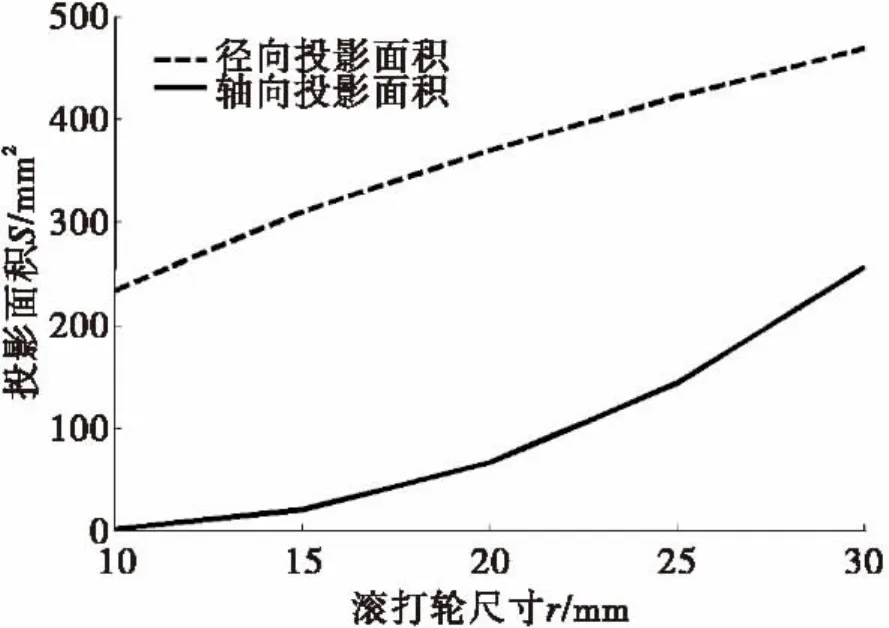
图9 滚打轮尺寸对接触面积影响Fig.9 The impact of roller size on contact area

图10可以看出，在滚打轮尺寸r小于15 mm时，轴向投影面积很小，且随r的增大接触面积增大非常缓慢，在该点之后随着r的增大轴向接触面积增加明显。由虚线可以看出随着r增加，径向投影面积变化近似成线性关系，而且该投影面积较大。

4 结论

(1)工件模数m在2～5之间时，切向投影面积S随模数增大趋势缓慢，而轴向投影面积与径向投影面积随模数增大而陡增，径向接触面积最大，其次是轴向投影面积，最小是切向投影面积。

(2)对模数为3的花键进行定量计算，由图可以看出对一横截面齿槽成形过程来说，各道次打入深度成线性递增关系，在打入深度0.6 mm之前，各道次递增面积增长缓慢，在该点之后接触面积发生指数形式陡增。

(3)滚打轮尺寸对接触面积影响主要体现在轴向投影面积和径向投影面积，滚打轮尺寸在r=15 mm之前对轴向投影面积影响甚微，在该点之后接触面积随滚打轮尺寸变化增加较大。而对于径向投影面积来说，滚打轮尺寸的递增与该投影面积近似呈线性递增关系，并且径向投影面积始终大于轴向投影面积。

参考文献:

[1]刘晋平，王宝雨，张康生，等.辊式楔横轧楔入轧制几何分析[J].塑性工程学报，2001(1):55-58.

[2]王友林，于青，姜英.齿轮轮齿齿廓渐开线的实用直角坐标方程研究[J].机械传动，2002(3):41-43.

[3]钱直睿.多点成形中的几种关键工艺及其数值模拟研究[D].长春:吉林大学，2007.

[4]崔凤奎.高速精密冷滚打成形技术研究[D].西安:西安理工大学，2007.

[5]束学道，张康生，胡正寰，等.楔横轧力能参数影响因素分析[J].重型机械，2002(4):29-33.

[6]SAFDARIAN R，MOSLEMINAEINI H.The effects of forming parameters on the cold roll forming of channel section[J].Thin-Walled Structures，2015，92:130-131.

[7]任秉银，唐余勇.数控加工中的几何建模理论及其应用[M].哈尔滨:哈尔滨工业大学出版社，2001.

[8]张大伟，李永堂，付建华.外花键冷滚压精密成形滚压接触面积的计算与仿真分析[J].太原科技大学学报，2007，28 (1):64-68.

[9]QIAN Z R，LI M Z，TAN F X.The analysis on the process of multi-point forming for dish head[J].Journal of Materials，2007: 517-520.

[10]DUFLOU J R，VERBERT J，BELKASSEM B，et al.Process window enhancement for single point incremental forming through multi-step toolpaths[J].CIRP Annals-Manufacturing Technology，2008，57(1):253-256.

[11]胡茂林.空间和变换[M].北京:科学出版社，2007.

[12]任玉杰.数值分析及其MATLAB实现[M].北京:高等教育出版社，2012.

Theoretical Calculation and Analysis on Contact Area of Spline Cold Precision Rolling

LIU Zhi-qi1，2，LU Hong-yu1，QU Bo1，WANG Wei-jie1
(1.School of Mechanical Engineering，Taiyuan University of Science and Technology，Taiyuan 030024，China; 2.Shanxi Key Laboratory of Metallic Materials Forming Theory and Technology，Taiyuan 030024，China)

The mathematical model of spline cold forming contact area was established by analyzing the metal deformation process，loading and boundary conditions of spline cold rolling，the theoretical calculation of contact area was got.The quick continuous plastic deformation of shaped parts occurs in the rolling mold.In order to make a research of technology mechanism and mechanic，the numerical relationship of workpiece feed rate and knock passes was established by analyzing contact process of roller and workpiece，and the relationship of workpicece feed rate and each pass knock depth was obtained，as well as the evolution of contact area.The numerical analysis software MATLAB was used to calculate and simulate the impact factor of contact area.

spline，contact area，mathematical model，numerical calculation

TH16;TG393

A

10.3969/j.issn.1673-2057.2015.04.002

1673-2057(2015)04-0250-05