基于单能射线的厚度测量系统合金补偿研究

张晓敏，吴志芳，张玉爱，苗积臣

（清华大学 核能与新能源技术研究院 核检测技术北京市重点实验室，北京 100084）

基于单能射线的厚度测量系统合金补偿研究

张晓敏，吴志芳，张玉爱，苗积臣

（清华大学 核能与新能源技术研究院 核检测技术北京市重点实验室，北京 100084）

针对高精度射线在线检测技术中存在的合金补偿问题，提出了窄束单能入射射线下合金补偿的理论计算公式，找出了合金补偿系数和厚度之间的规律。通过实验方法测量了实际系统中的合金补偿系数，验证了理论分析的正确性。利用蒙特卡罗程序MCNP5建立几何模型进行仿真实验，结果和理论分析相一致，与实验结果亦相似，说明几何模型能准确反映实际情况，可替代实验。对实验和仿真结果按照理论参考值进行合金补偿，补偿效果明显，1.25MeV射线能量下304不锈钢相对测量误差从约1%减小至约0.1%。

合金补偿；单能射线厚度测量；蒙特卡罗方法

随着我国冶金钢铁行业的迅速发展和对高质量、高精度板带材产品需求的急剧增加，高精度检测设备已广泛应用于大型现代化钢铁企业。高精度射线测厚仪和凸度仪作为一种线度测量系统，能实时反馈钢板的中心厚度、断面轮廓、纵向平直度及宽度等信息［1－2］。清华大学核能与新能源技术研究院成功研制出国内首个具有自主知识产权的X射线凸度仪，各项性能均达到国际标准［3－4］。

合金补偿技术作为射线在线检测技术的一个核心问题制约着测厚仪与凸度仪的工业应用［5］。钢铁行业板材的型号多样，各型号的化学组分差异很大。因此在高精度测量系统中，必须考虑测量对象的材料变化对测量结果的影响［2，67］。国内大型钢铁企业引进的相关设备均采用现场采集的方法实现校正［8］，方法适用范围小，成本大，亟待建立一个完备的研究模型。

射线法测厚依赖X或γ射线与物质相互作用的过程实现测量目的。射线可分为单能射线和连续能谱射线，由于连续能谱射线的能谱信息不易获取，与物质作用过程中存在能谱硬化等特殊现象的影响，而单能射线能量单一，与物质作用过程简单，因此在一般科学研究中首先考虑单能射线，根据单能射线的研究结果再进一步研究相对复杂的连续能谱射线。本文探究单能射线下测厚系统的合金补偿方法。

1 合金补偿及相关理论分析

对于射线法厚度测量系统，一般均需利用某种材料的标定板对其进行刻度［9］。从理论上讲，若要测量准确，选取的标定材料和测量材料应一致，从而保证对应数据之间的一致性。但在实际测量中，对标定板有极为严格的精度要求，不可能针对每种材料均制取相应的标定板。大多数情况下，测量材料和标定材料不同，测量厚度不能代表实际厚度，需对其进行相应的校正。

假设材料实际厚度为xcoil，未进行合金补偿的测量厚度为xmeasure，通过引入补偿系数s将测量厚度校正到实际厚度，则：

根据射线与物质的相互作用原理，窄束单能X或γ射线在物质中遵循指数衰减规律，有：

其中：I0为入射前的射线强度；I为被物体吸收后的射线强度；x为物体的厚度；μ为物体的线性吸收系数［10］。

对式（2）进行变换即可得到x与射线强度之间的关系：

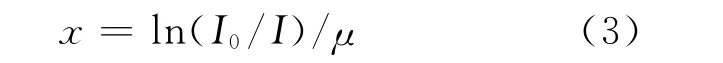
则有：

其中：μcoil为测量材料的线性吸收系数；Icoil为通过测量材料后的射线强度。

在实际测量中，测量厚度按式（5）计算：

其中，μbase为标定材料的线性吸收系数。

根据式（1）、（4）、（5）可得到单能射线下合金补偿系数的理论计算式：

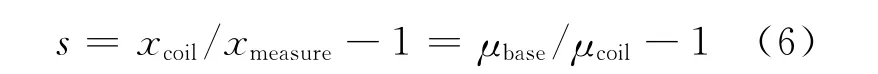
由式（6）可知，在窄束单能入射射线下，合金补偿系数仅由两种材料的线性吸收系数决定，不受吸收材料厚度的影响。

合金材料一般由多种元素按照一定的质量比组成，其在单能下线性系数可通过式（7）确定：

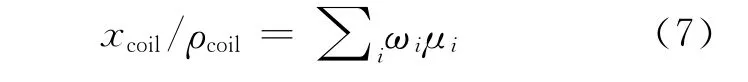
其中：ωi为第i种元素的质量百分比；μi为第i种元素在该能量下的质量吸收系数［11］。

本文以纯铁为标定材料，研究304不锈钢的合金补偿系数。304不锈钢的化学成分为：C，0.046%；N，0.049%；Si，0.43%；P，0.028%；S，0.001%；Cr，18%；Mn，1.16%；Fe，72.266%；Ni，8.02%。参考美国国家标准与技术研究院数据库提供的各元素质量吸收系数，按式（6）、（7）可计算出304不锈钢在1.25MeV下的合金补偿系数的理论参考值为－0.009 2。

从式（6）、（7）可知，射线源能量、所含合金元素及元素含量是影响合金补偿系数的主要因素。

2 蒙特卡罗模拟实验

2.1 MCNP5几何模型

MCNP5建立的几何模型如图1所示。在模型中，射线源发出的γ射线与吸收材料发生作用后，经准直器进入探测器。其中，射线源为能量1.25MeV的理想点源，射线出射方向为小角度锥形束；吸收材料为不同厚度的规则长方体板，其材料分别为纯铁和304不锈钢，纯铁用来模拟标定材料，304不锈钢用于模拟测量材料；准直器为中心带孔的铅板，探测器为体单元模型，其计数采用F4卡，记录通过探测单元的粒子通量。为保证模拟结果的精确度，源粒子数设置为2×108。

图1 MCNP5几何模型示意图Fig.1 Scheme of MCNP5geometrical model

2.2 模拟结果及处理

1）系统刻度

模拟中将纯铁作为标定材料，分别模拟2～40mm之间共20组厚度。对模拟结果进行相关处理后得到系统的刻度曲线，结果示于图2。

由式（3）可知，x与ln（I0／I）呈线性关系，因此对于窄束单能射线测厚系统，其系统刻度曲线应为直线。图2所示的模拟结果符合上述推断，证明几何模型能达到窄束测量系统的标准，模拟结果可信。

2）304不锈钢模拟结果及合金补偿系数的测量

图2 蒙特卡罗模型刻度曲线Fig.2 Calibration curve of Monte Carlo model

利用图2所示的刻度曲线对304不锈钢的模拟结果进行测量，测量结果列于表1。在各厚度下，对304不锈钢的测量值均比实际值偏大，相对测量误差在0.8%～1.2%之间。根据测量厚度和实际厚度，利用式（6）计算出各厚度下的合金补偿系数，计算结果如图3所示，合金补偿系数随厚度在某值附近波动。对数据点进行线性拟合，拟合结果是值约为－0.009 5的水平线，与理论值－0.009 2的差别不大。模拟计算的合金补偿系数随厚度的波动是由模拟系统本身的统计涨落所造成，通过加大模拟粒子数目的办法可减小波动。

表1 蒙特卡罗模型厚度测量结果Table 1 Thickness measured by Monte Carlo model

图3 蒙特卡罗模型的合金补偿系数Fig.3 Alloy compensation coefficient of Monte Carlo model

对于单能测厚模拟系统，若不考虑本身的统计涨落，可认为模拟得到的合金补偿系数不随厚度变化，与理论值相符合。对测量厚度按理论值进行合金补偿，补偿结果列于表1，补偿后的测量值更加接近实际值，相对测量误差大部分在±0.1%以内。

360Co放射源实验研究

3.1 实验平台介绍

实验依托清华大学核能与新能源技术研究院研制的集装箱CT系统为平台，对不同厚度的纯铁板和304不锈钢钢板进行测量。实验平台的放射源为60Co（可近似认为其为1.25MeV单能射线），探测器为充气电离室，钢板和探测器之间通过钨板和铅块实现准直。

3.2 实验结果及处理

利用纯铁对系统进行刻度，测量结果和刻度曲线如图4所示。纯铁厚度与ln（I0／I）呈良好的线性关系，但同模拟结果及理论值相比，刻度曲线在纵轴截距不为零，这说明系统不属于严格意义的窄束射线，准直器未完全遮蔽散射射线，在利用此刻度曲线测量304不锈钢钢板厚度时需对曲线和探测器输出进行处理。

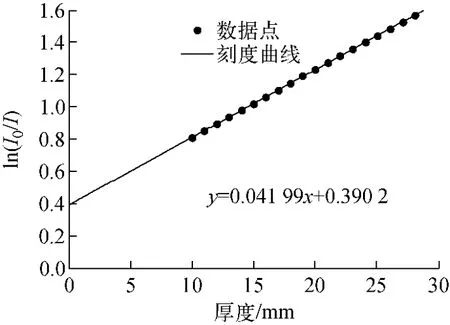
图4 实验平台刻度曲线Fig.4 Calibration curve of experiment system

利用实验平台刻度曲线对304不锈钢的实验测量数据进行测量，测量结果列于表2。同模拟结果类似，实验测量值均比实际厚度偏大，相对测量误差在0.5%～1.8%之间。图5为304不锈钢合金补偿系数的实验测量结果，在10～40mm的厚度范围内，合金补偿系数在－0.01附近波动，对数据点进行线性拟合，拟合结果呈良好的水平线，说明合金补偿系数的实验测量结果有不随厚度变化的趋势。

表2 304不锈钢实验测量结果Table 2 Thickness measured by 304stainless steel experiment system

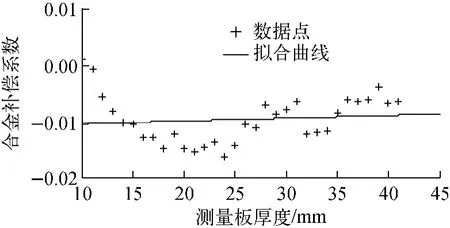
图5 实验测量的合金补偿系数Fig.5 Alloy compensation coefficient measured by experiment system

实验测量的合金补偿系数随厚度有一定的波动，这种波动与材料的化学成分无关，而是射线源的稳定性、散射及周围实验环境等共同影响的结果，通过严格控制实验条件可减小这种波动。

在单能测厚系统中，去除其他因素的影响，可认为实验测量的合金补偿系数不随厚度的变化而变化，与理论分析相符合。对测量结果按理论值进行合金补偿，补偿结果列于表2。经过补偿，相对测量误差减小约1个数量级。

4 结论

本文分析了在单能射线厚度测量中存在的合金补偿问题，得到了合金补偿系数的计算公式。在窄束单能射线下，系统的合金补偿系数由两种材料的线性吸收系数共同决定，且不受材料厚度的影响。

通过建立MCNP模型进行了模拟实验，模拟结果从定性和定量两方面验证了理论分析结果。从定性来说，单能测厚系统的合金补偿系数与厚度无关；从定量来讲，通过两种材料的线性吸收系数计算得到的合金补偿系数理论值同模拟测量结果相近，采用理论值对测量结果进行校正能达到测量目的。通过60Co实验平台测量了实际系统的合金补偿系数，实验结果与模拟结果及理论分析结果相符合。

［1］ 何斌.热轧生产中的X射线板型测量技术［J］.新疆钢铁，2010（2）：33-35.HE Bin.

Application of X-ray profile measuring technique in hot strip mill of bayi steel［J］.Xinjiang Iron and Steel，2010（2）：33-35（in Chinese）.

［2］ 朱秋峰，张新燕，李大安.X射线测厚技术在热轧钢板生产中的应用［J］.无损检测，2008，30（5）：321-323.

ZHU Qiufeng，ZHANG Xinyan，LI Daan.Application of X-ray measuring technique in hot strip mill［J］.Nondestructive Testing，2008，30（5）：321-323（in Chinese）.

［3］ 苗积臣，吴志芳，张玉爱，等.凸度检测系统厚度测量精度分析［J］.原子能科学技术，2011，45（8）：983-986.

MIAO Jichen，WU Zhifang，ZHANG Yuai，et al.Research of thickness measure precision in X-ray profile gauge［J］.Atomic Energy Science and Technology，2011，45（8）：983-986（in Chinese）.

［4］ 苗积臣，吴志芳，邢桂来.凸度检测系统中X光机参数对厚度测量精度的影响［J］.原子能科学技术，2011，45（9）：1 112-1 115.

MIAO Jichen，WU Zhifang，XING Guilai.Effects of X-ray tube parameters on thickness measure precision in X-ray profile gauge［J］.Atomic Energy Science and Technology，2011，45（9）：1 112-1 115（in Chinese）.

［5］ ARTEM’EV B V，MASLOV A I，POTAPOV V N，et al.Use of X-ray thickness gauges in manufacturing rolled non-ferrous metals［J］.Russian Journal of Nondestructive Testing，2003，39（6）：55-61.

［6］ 魏运鹏，方伟新.X射线测厚仪测量精度影响因素及补偿措施［J］.自动化仪表，2011，32（10）：79-81.

WEI Yunpeng，FANG Weixin.Factors influencing measurement accuracy of X-ray thickness gauge and appropriate compensation measures［J］.Process Automation Instrumentation，2011，32（10）：79-81（in Chinese）.

［7］ 高飞，王磊，申凌云，等.RM312板形仪厚度精度及稳定性的提高［J］.自动化应用，2011（6）：9-10.

GAO Fei，WANG Lei，SHEN Lingyun，et al.Improvement of thickness measurement accuracy and stability of RM312shape meter［J］.Automation Application，2011（6）：9-10（in Chinese）.

［8］ 杨建华，刘文琦，郎华威，等.同位素测厚仪的合金曲线标定方法的研究［J］.仪器仪表学报，2004，25（4）：725-726.

YANG Jianhua，LIU Wenqi，LANG Huawei，et al.A new method of calibrating alloy curve of isotope thickness gauge［J］.Chinese Journal of Scientific Instrument，2004，25（4）：725-726（in Chinese）.

［9］ 邢桂来，张玉爱，苗积臣.凸度仪校准片厚度序列选取的理论分析和仿真［J］.原子能科学技术，2011，45（10）：1 247-1 249.

XING Guilai，ZHANG Yuai，MIAO Jichen.Theory analysis and simulation of thickness series for reference samples used in calibration of X-ray instantaneous profile gauge for steel strip［J］.Atomic Energy Science and Technology，2011，45（10）：1 247-1 249（in Chinese）.

［10］安继刚.电离辐射探测学［M］.北京：原子能出版社，1995.

［11］杨福家.原子物理学［M］.北京：高等教育出版社，2008.

Study on Alloy Compensation for Thickness Measurement System of Monoenergetic Radiation

ZHANG Xiao-min，WU Zhi-fang，ZHANG Yu-ai，MIAO Ji-chen
（Beijing Key Laboratory on Nuclear Detection ＆Measurement Technology，Institute of Nuclear and New Energy Technology，Tsinghua University，Beijing100084，China）

To solve the problem of alloy compensation for high accuracy radiographic inspection technique，a calculation formula of alloy compensation coefficient was presented and the relation between alloy compensation coefficient and thickness was found.The alloy compensation coefficient measured by an isotope thickness measurement instrument indicates that the theoretical analysis results are correct.A geometric model was built by MCNP5based on the Monte Carlo method.The simulation results are consistent with the theoretical analysis results.It proves that the model is accurate and the method to calculate the alloy compensation coefficient is feasible.To compensate the experimental and simulated thickness with the calculated alloy compensation coefficient，the relative measurement error of 304stainless steel decreases from about 1%to 0.1% at 1.25MeV.

alloy compensation；momoenergetic radiation thickness measurement；Monte Carlo method

TL99

：A

：1000-6931（2015）05-0930-05

10.7538／yzk.2015.49.05.0930

2014-01-15；

2014-05-08

张晓敏（1987—），男，甘肃庆阳人，博士研究生，核技术及应用专业