八方联系智慧现浑然一体高效生
2015-05-25安徽省灵璧第一中学郑良
☉安徽省灵璧第一中学 郑良
八方联系智慧现浑然一体高效生
☉安徽省灵璧第一中学 郑良
一、问题提出
社会一方面要求教育必须减轻学生负担,另一方面对人才能力的需求越来越高.如何解决这对矛盾,唯有提高课堂教学效率.“教学效率需从两个维度来认识:在学生的时间投入方面,指能够充分利用实践,全身心、主动地参与数学学习;在数学结果方面,指多方面学习效果——认知成绩、理性精神、效率意识、良好的认知结构和数学学习能力.教学效率是相对概念,同样的学习结果,学习时间较少,则教学效率高.同样的学习时间,学习的效果好而且多样,则教学效率高.”[1]反观我们的课堂,师传生受的教学现状使课堂发展是线性的、波澜不惊的.这种对知识、思想方法的“填鸭”式灌输的教学,学生没能切身体验到思维历程和感悟到认知冲突的历练,从而导致“懂而不会”现象的不断产生.“探索是数学教学的生命线”(布鲁纳语),探索是一个曲折的过程,是失败与成功交融的辩证统一过程,是师生之间的互动过程.追溯成因、探寻解决方案具有重要的现实意义.基于上述分析与思考,笔者选取了如下问题进行探究:


二、情境再现
限于篇幅,下面的所有讨论都只对a≠0展开.为真实呈现教学情境,现以师生对话形式再现课堂实录.
师:对于本题的条件和结论,你有哪些想法?(学生思考后)
生1:对任意不同时为零的实数a,b,f(x)=0至少有一个根在(-1,0)内.设f(x)=0的两个根分别为x1,x2,且x1<x2,通过x1∈(-1,0),x2∈(-1,0)分别找出a与b的关系
生2:思路可取,过程繁杂.
师:生1的想法非常自然、接地气.朴素的解法过程如何呢?绝知此事要躬行.(展示生1的解题过程)
证法1:当a≠0时,则有f(x)=a(3x2+2tx+t-1).记h(x)= 3x2+2tx+t-1,其Δ=4(t2-3t+3)>0,设h(x)(f(x))的两个零
由-1<x1<0
①当t≤0时,平方得t2<t2-3t+3<t2-6t+9,解得t<1,则t≤0;
③当t>3时,不等式无解.
综上所述,由x1∈(-1,0)得t∈(-∞,2).
同理,由x2∈(-1,0)得t∈(1,+∞).因此,当t∈(-∞,1]∪[2,+∞)或t∈(1,2)时,函数h(x)在(-1,0)内分别有1个,2个实数根,即函数y=(fx)在(-1,0)内至少有一个零点.
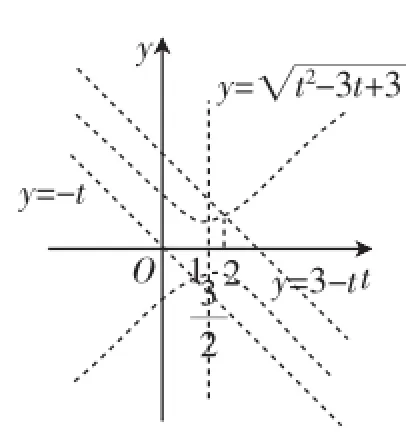
图1
生2:生1的处理比较“精细化”,结论中“至少”提示我们可用并集概念“模糊化”进行整体考量,即(-∞,2)∪(1,+∞)=R.生1从数的角度对不等式进行求解,导致只见树木不见森林,需要分类讨论;若能利用形的整体与直观,运算具有针对性,可提高解题效率.
(师生共同完善生2的解题过程)
生3:结论中“至少有一个零点”中的“至少”提示我们可以尝试用反证法来证明.
①当x1≥0时,x1x2≥0,x1+x2≥0,故s>2,与s=0矛盾;
②当x2≤-1时,s=3(x1+1)(x2+1)+3x1x2-1>2,与s=0矛盾;
③当x1≤-1,x2≥0时,s=3(2x1+1)x2+3x1+2<0,与s=0矛盾.
综上所述,假设不成立,即原命题成立.
师:(追问生3,针对如此变形的思维过程,少数学生可能会遗漏③)反设的结果是原结论的反面(补集),必须一一驳斥,能根据具体数式等进行合理变形,导出矛盾是证明的关键.
生4:“闭区间上连续函数零点定理”是判定“连续函数y=f(x)在区间(a,b)内至少有一个零点”的充分不必要条件.欲使函数y=f(x)在区间(a,b)内至少有一个零点,可转化为函数y=f(x)在(a,b)的子区间(c,d)内至少有一个零点.利用二次函数的(最值)性质,可尝试用区间的中点与端点的函数值(二分法)进行判断.综上所述,函数y=(fx)在(-1,0)内至少有一个零点.生5:生4将f(-1)(f0)巧妙变形,合理分解,只需判2断的取值范围,当然还可以将其细化.二次函数的最值只能在端点处或顶点处取得,利用端点和顶点对应的函数值的关系是解题的方向,更能反映问题的本质.

①若t>2或t<1时,(f-1)(f0)=-a(2t-2)(t-1)<0,则函数y=(fx)在(-1,0)内至少有一个零点.
②若t=1时,(fx)=ax(3x+2)的零点分别为-2,0,符3合题意;若t=2时,(fx)=a(3x+1)(x+1)的零点分别为,-1,符合题意.
③若1<t<2时,(f-1)(f0)>0,(fx)的对称轴所以(fx)在(-1,0)内至少有一个零点.
综上所述,函数y=(fx)在(-1,0)内至少有一个零点.
师:生5将问题进行分解,对f(-1)f(0)>0,能结合函数的对称性、最值,准确定位,合理解剖.下面我们共同探究参考答案的思维历程.
生6:本题转化为函数y=f(x)在(-1,0)的子区间内至少有一个零点.可用待定系数法得到问题的通解,赋值法体现了特殊与一般的逻辑关系.
探究目标:设m,n∈[-1,0],且m≠n,使得f(m)f(n)<0.

师:精彩!赋值是操作,是逻辑推理的显性化.根据题意如何取值往往涉及解方程(组)等.例如,f(x)在(-1,0)内至少有一个零点,必存在一个数,其函数值(-1,0).
当a≠0,b≠0时,记a=(0,a),b=(b,0),则向量m,n的“故事”,才能做到知其然并知其所以然.
生7:由上面方程组,联想到共线(反向)向量,可得如下证法.
证法6:当a≠0,b=0时,f(x)=3ax2-a的零在基底{a,b}下的坐标分别为m=(2m+1,3m2-1),n=(2n+ 1,3n2-1),由题意知m,n共线(反向).

师:生7由方程组的结构特征,联想到向量,(通过坐标变换)从图形的角度给出解释.
生8:本题的命题背景为高等数学的罗尔中值定理(若函数F(x)满足如下条件:①F(x)在闭区间[a,b]上连续;②F(x)在开区间(a,b)内可导;③F(a)=F(b).则在(a,b)内至少存在一点ξ,使得F′(ξ)=0).
证法7:设F(x)=ax3+bx2+(b-a)x,则F′(x)=f(x)=3ax2+ 2bx+b-a.又函数F(x)在闭区间[-1,0]上连续,在开区间(-1,0)内可导,且F(-1)=F(0)=0,由罗尔中值定理可知,至少存在一个实数ξ,使得F′(ξ)=0,即y=f(x)在(-1,0)内至少有一个零点.
三、教学感悟
1.高效课堂应强调先进理念的引领
在界定“高效课堂”时,我们需要不断地返回到时代精神之中,用新的理念、新的观点去诠释课堂,追求的应该是一个动态的、发展的过程.如给每个学生话语权,对话是思维交流的重要方式.案例中生1想法朴实,过程稍显烦琐,引来学生笑声,教师不为了进度而剥夺其话语权,取而代之与学生一起聆听其思维发生、发展、完善的过程,生2准确理解并能灵活运用并集概念,对数形结合思想认识深刻,生3变形巧妙说明其对目标与方向把握精准.通过“挤”出学生想法,深入理解学生,以学定教.教师要信赖学生,敢于放手,尝试通过教师的“无为”促使学生的“有为”,如每个学生均给出不同的证法,课堂上群策群力,还给出其他证法,例如,利用平均值原理0等.同时要善于向学生(教育服务对象)学习,在做好学生学习帮助者的同时坚信每位学生不仅能帮助自己完成教学任务,还能帮助自己提高教学水平.又如,教学评价的目的不是为了证明(互动),而是为了改进.评价的根本目的是反馈交流,促进师生反思、改进,促使其完善、发展,从而保证课程目标的实现.
2.高效课堂应关注课堂系统的优化
研究高效课堂,其目的不是去构建一个普适性的、通用型的教学模式,而是引导教师结合具体的教学情境选择和创新最优化的教学设计.例如,尽可能站在学科系统的高度,着眼于知识之间的联系和规律,着重于哲理观点的升华;选取典型的问题,不断变式,进行一题多解,多解归一,多题归一,使学生能自觉地运用联系的视角看待问题,透彻地理解分析问题,高端的观点处理问题,例如,案例中教师穿针引线,引领学生巩固知识、感悟思想方法、澄清认识,能从局部和整体分析与解答问题,切实提升学生的智慧.乌申斯基说得好:“智慧不是别的,只是组织得很好的知识体系.”当学生的头脑“强大”了,在问题面前“运筹帷幄”、“纵横捭阖”,难题自然“无处遁形”、“落花流水”了.
3.高效课堂应聚焦教学行为的转变
美国当代管理理论大师阿吉里斯曾使用“使用理论”和“信奉理论”两个不同的概念来区分人们的“行为”与“认识”之间的差距.即人们口头上陈述的往往是自己的“信奉理论”,而事实上指导他们行动的却是“使用理论”.很多教师对转变教与学方式表示认同,但真实的课堂却依然如故.这就启发我们高效课堂的研究不能局限于观念的认识,而应该外化为教学的行为.当前教学中,很多教师能向学生交待思维过程,期待学生从看到的过程中领悟问题本质,少数教师只对答案进行告知,缺乏正确的解读.清末数学家华衡芳主张暴露思维过程,“一切算法无不坦白示人”,一切解法“不求简奥,不避粗俗,惟使人易明而已”.不避粗俗,是指解题过程中不可避免的弯路;不求简奥,是指简奥来自于挣脱困境的反思,否则,学生只能陶醉在“简奥”之美而受益甚微.“当时,希尔伯特(Hilbert)选听富克斯(Fuchs)的课.他的课确实与众不同,给人的印象至深.课前,他不大做准备,因为他习惯于在课上把自己置于险境:对要讲的内容,现想现推.正如他的一个学生后来写的那样,学生因此而‘得到了一个机会,瞧一瞧最高超的数学思维的实际过程’.”[2]这种教师(原生态)的真实思维过程,使学生终身受益.教师要躬亲示范,促使学生从模仿到自觉领悟.
4.高效课堂应源于三个理解能力的落实
魏书生老师曾说过:“学生的能力是学出来的,不是教师教出来的.”但学生是向教师学习的,教的方式决定着学的方式,教的深刻,学的透彻,教有深度,学有高度.教师的高度决定学生的高度,教师“三个理解”的水平决定着教学的水平.[3]任何教师都想让自己的学生更出色,但教师的水平成为左右学生发展的瓶颈.“以己昏昏,岂能使人昭昭.”没有对数学、教学、学生等准确的理解,理念、行为犹如无源之水,高效课堂乃是空中楼阁.教师要终身学习,不断研究,积累高效课堂的前提与基础.如生8给出的罗尔定理就是笔者分层教学指导的结果.如教师对高等数学的理解程度决定着教学的高度、深度与广度,如罗尔定理的几何意义、闭区间套定理的极限逼近思想、洛比达法则等.数学教育学家张奠宙先生说:“在日常的中学数学教学中,能够用高等数学的思想、观点、方法去解释和理解中学数学问题的例子很多,重要的是,作为一名数学教师应该具有这样的思维意识.”
尽管教学理念得以发芽生根,局部探究得以实现.但必须提及的是,案例问题的初步思考是在课下进行的,课堂探究方式方法也不成熟,课堂优质高效尚未完全落实.教学是科学,也是艺术.教学技能反映着教学作为科学的一面,而教学智慧则展现着教学作为艺术的一面.因此,高效的课堂既需要教师专业化的行动策略,也需要教师个性化的教育智慧.
本文的撰写,得到天津师范大学津沽学院刘伟老师、江苏省睢宁县古邳中学苗勇老师的帮助,笔者在此表示衷心的感谢!
1.王光明.重视数学教学效率提高数学教学质量——“数学教学效率论”课题简介[J].数学教育学报,2005(8).
2.【美】康斯坦丝·瑞德(ConstanceReid),著.希尔伯特——数学世界的亚历山大[M].袁向东,李文林,译.上海:上海科学技术出版社,2006.
3.渠东剑.三谈启发思维重于诱导结果[J].中学数学教学参考(上),2015(4).
5.苏鸿,主编.高效课堂[M].上海:华东师范大学出版社,2013.
6.孙维刚.如何让学生聪明起来[J].中小学管理,1999(10).
7.王锋,郑良.关于数学“一题多解”教学的辩证思考[J].中学数学(上),2015(1).F
