波利亚解题模型在高中数学解题教学中的应用

☉浙江省嵊州市黄泽中学 袁钢南

波利亚解题模型在高中数学解题教学中的应用

☉浙江省嵊州市黄泽中学 袁钢南

21世纪我国基础教育进入到新课改时代，想要对当前时代发展需求有效满足，就必须要对传统应试教育中存在的问题彻底改善，教学目标集中在培养学生健全人格上，在这一基础上就要完善新的基础教育体系.其中在高中数学解题教学过程中，对波利亚解题模型进行应用，有助于引导学生正确把握数学解题思路.波利亚解题模型体现了它的解题思想，它的解题思想主要表现为四个过程阶段：阅读题目、理解题目；得出解题思路、制定解题计划；实施解题计划；回顾解题过程.清楚了这种模型的具体解题思路之后，我们将以具体实例来阐述这种模型的运用.

一、波利亚解题模型的理论研究

波利亚是一位经典分析大师，在变分学、概率论及函数论等多方面有深入研究，波利亚解题思想较丰富，其中最为经典的专著有《数学的发现》、《数学与猜想》及《怎样解题》等，其中《怎样解题》中的解题模型及解题表具有重要的应用价值.在波利亚解题模型中，将解题过程分为四个阶段，即理解问题、制定计划、实施计划及回顾分析.其中第一阶段，理解问题要弄清已知条件是什么，问题是什么.如：解决应用题时，采用数学语言将题目描述出来，并且还要对其中的已知条件和未知条件等明确.在对题目弄明白之后，就要对大脑中的相关知识点进行搜索定位，确定具体的解决方式.第二阶段就需要针对这些问题制定相应的计划，应理解条件中各个要求有怎样的联系，或者未知量与已知量有什么关系等.可从寻找模型、寻找技能、转化题目三方面进行，也是指找到与此题目相类似的问题，并从相关解题中获得启发，深入分析题目的问题及条件等，查看是否有合适的思想方法及技能，尤其在遇到较为复杂的问题时，可将其转换为比较熟悉的模型，对其进行解决.第三阶段，实施制定的计划，在已形成的解题思路及解题方案的指引下，采用已学知识、技能及原理等解决问题.第四阶段，则需要对整个解题过程进行回顾性分析及总结，主要要求学生怎么理解问题，形成怎样的解题思路，以及如何检验所得问题的结果，本题是否还隐藏有其他的解决办法.

二、波利亚解题模型在高中数学解题中的常用模式

1.叠加模式

这种模式通常是将其具体情况分解成相关的几个特殊情况组合，或者是把相关的特殊情况全部叠加在一起集合成为一般情况，之后采用相适应的方式对其进行解决.

例1如果一个物体做抛物线运动，其轨迹如图1所示，那么将其初始速度设置成v，求物体运动曲线的轨迹方程.

解析：关于这一题目可采用叠加模式进行解决，由于物体的运动轨迹是一条曲线，并不是圆弧.当一质点在水平方向实施匀速直线运动的时候，如果运行t秒之后，那么其位移则可以用公式x=vt表示，但是关于其运动轨迹也可以将其看成是两种运动

图1

2.递归模式

这种模式应用通常是在数列求和中，在高中数学解题中此类题型是较为常见的题，解决此类题目时需要应用递归模式.

例2求S2=12+22+32+42+52+62+……+n2的和.

解析：针对此题的解题方式我们可采用递归模式来进行求解，此时，公式（n+1）3=n3+3n2+3n+1，从而得出（n+ 1）3-n3=3n2+3n+1，将具体数值带进去，即可得到23-13=3× 12+3×1+1；33-23=3×22+3×2+1，43-33=3×32+3×3+1，…，以此类推，即可得到（n+1）3-n3=3n2+3n+1，将两边相加，得到（n+1）3-1=3S2+3S1+n.最后将S1带入到上式中，可得到

3.双轨迹模式

这种模式通常是在数学几何解题中应用，可以将问题成功转化成一个点进行解决，依照具体条件能够将其分成若干部分，不管是哪一个部分都可以将其转化成为点的轨迹，并且每一个点的轨迹可以是一条直线，也可以是一个圆等，在对满足条件的若干轨迹的交点也即是需要求解的问题.

例3已知三个相等并且不在同一直线上的圆，作一圆使得包含其他三个，并且与三个圆均相切.

解析：对于此道题，要想实现与其他三个圆均相切，则必须找到相应的圆心及半径即可，根据圆心及半径作圆就较为简单.因此，本题的解题关键就是寻找圆心及半径.可假设作出图2.在该图中O假设为要找的圆心，而O1、O2、O3为已知圆的圆心，其中A、B、C均为切点.即OA= OB=OC，所代表的也就是圆的半径.之后，依照以上题目中的已知条件，可以得到三个小圆的半径均相等，即O1A=O2B=O3C，也表示OO1=OO2=OO3.这样一来，将问题转化为：已知圆心O1、O2、O3三点，作与它们的距离相等的点O，如图3，换句话来说，求出△O1O2O3外接圆的圆心.最终，将此道题可转换为我们之前解答的题目，就可以很简单地将圆作出来了.

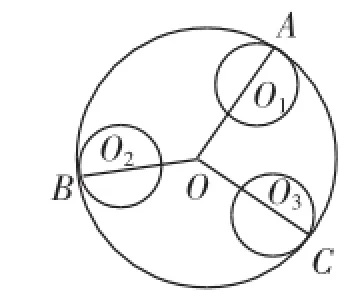
图2

图3

三、高中数学解题中应用波利亚解题模型的基本思路

1.理解题目

理解题目就要理解题目给出的条件，理解题目的语言陈述，首先要清楚已知数据、未知条件和题干条件都分别是什么.进而要深层次地分析题目，弄清题目中的细节，对要求的问题进行定位.学生在清楚明白这些要求和条件之后，就要思考解题思路、运用数学方法进行解题.下面将以实例对理解题目进行详细的阐述.

例4将直线2x-y+λ=1沿x轴向右平移1个单位，所得直线与圆x2+y2+4x-2y=0相切，求实数λ的值.

（1）首先，这道题目自身就是用数学语言来表达的题目，所以不用将其转化为数学问题.

（2）然后，我们可以得知条件有两个，一是直线2xy+λ=1沿x轴向右平移1个单位，另一个是平移之后的直线与圆x2+y2+4x-2y=0相切，问题是求出实数λ的值.

（3）题干条件和所要求的问题都清楚明白之后，就需要对题目范围进行判定.将两个具体已知条件列出来，将题目答案的范围确定，应为实数.

2.解题思路与解题计划

制定解题计划是这一步的主要任务和内容，对于问题的理解之后，就是构思解题思路，形成良好的解题思路需要良好的知识储备和经验储备，加强对模型的积累和思想方法、技能的积累，制定思路时可以想想是否曾经遇到过相似的题目，看是否能从中得到一些启示，来形成自己的解题思路.解题思路和解题计划的制定需从三方面入手：寻找类似的模型；寻找相关的技能和思想方法，对题目条件进行深入思考分析，看是否有相应的技能和思想方法；将题目进行适当的简化与转化，转化为熟悉的模型，然后进行解题.

例5已知a1=2，an+1=2an+5n，求数列｛an｝的通项公式.

（1）第一步是将解题思路具体化，找出解题的合适模型.通过观察题干给出的条件，我们可以选择待定系数法来进行构建新模型，可推出参考量an+1=2an+5n，然后再构造出新数行数学计算解答.

（2）找到类似的模型之后，就需要将现有不熟悉的模型转化为简单熟悉的解题模型，转化模型本题要用的是待定系数法，那么应使第三项变为常数项，因此将两边同除以5n，得而转化为5bn+1-2bn=1这种模型来解题.

3.实施解题计划及解题回顾

实施解题计划是具体的实施过程，实施过程中会遇到各种各样的问题，所以在进行实施解题方法时，我们应该认真思考以前解题时可行的代数或者是几何运算，用形式推理或者是直接观察，再或者是两者的结合将解题步骤确定并进行检验，将解题思路与方法在具体运算中高效地结合

解题回顾，顾名思义就是在解决完一个问题后回过头来检验自己的解答过程和解答的答案是否正确，这是经常被学生和教师忽略的.做题不能只是做题，还要从做题中深层次地挖掘出一些可总结、可利用的东西，这些东西可以指导着以后求解的其他问题，解题者不能只停留在对当前这一个问题的解答，而是要深入理解和思考如何解答这个问题，以及寻找更加简便的解题思路和解题途径，对于解题过程中的障碍要充分发挥已学知识和数学思想的作用，使解题更快更对.