圆柱耐压壳基座板厚对振动传递性能的影响

温华兵，刘林波，吴晨晖

(江苏科技大学振动噪声研究所，江苏 镇江 212003)

圆柱耐压壳基座板厚对振动传递性能的影响

温华兵，刘林波，吴晨晖

(江苏科技大学振动噪声研究所，江苏 镇江 212003)

建立耐压圆柱壳体及平台结构的有限元模型，引入实验与有限元模型的传递函数相关系数，进行传递函数相关系数灵敏度分析，修正圆柱壳体的有限元模型，使圆柱壳体结构的前10阶固有频率的计算误差小于8%，在800 Hz低频率范围内传递函数计算与实验结果的幅值误差小于3 dB。在基座板厚对传递函数灵敏度分析的基础上，探讨基座板厚对振动传递的影响。

基座;传递函数;相关系数;灵敏度;模态;有限元

在对结构进行有限元建模时，常忽略板材之间焊接焊缝对结构的影响，对一些复杂的局部结构加以简化，将一些难以确定的参数用等效方法处理，从而不可避免地带来计算误差。有限元模型的建模和简化方法，将直接影响到计算结果的准确性。因此，有限元模型的修正，对复杂结构的动态特性进行准确的预测是很重要的，目的是使有限元模型与实验数据相一致。灵敏度分析是一种评价因设计变量或参数的改变而引起目标函数特性敏感程度的方法。已有的讨论集中于车身阻尼层结构的声灵敏度分析及优化［1］，振动传递路径的功率流传递度灵敏度［2］，采用摄动法研究各向异性圆柱壳体的非线性振动特性［3］，双层圆柱壳噪声预报及统计能量参数灵敏度分析［4］，文献［5-9］研究了基于频响函数相关性的灵敏度分析的有限元模型修正方法。本文考虑采用传递函数相关系数灵敏度方法，修正圆柱壳体及基座结构的有限元模型，分析基座参数对振动传递特性的影响。

1 有限元模型的修正方法

采用相关分析，可以比较有限元与实验结果的一致程度，由于传递函数包含了结构的特征频率、振型和阻尼特性，选用传递函数作为修正的目标，可较全面地修正有限元模型的结构动态特性。在频响函数的每一个频率处，用形状相关系数和幅值相关系数来描述计算和测试传递函数之间的相关性。形状相关系数定义为

式中:He(ωi)——在频率ωi处实验的传递函数;

Ha(ωi)——在频率ωi处计算的传递函数。

形状相关系数表示数值计算和测试传递函数之间的形状相关程度，主要由共振峰值的位置和数量决定，与模型的刚度和质量参数灵敏。传递函数不仅与形状有关，还与幅值密切相关，再引入幅值相关系数

幅值相关系数表示数值计算和测试传递函数幅值之间的相关程度，与模型的阻尼参数灵敏。形状相关系数和幅值相关系数的取值范围在0～1之间，当大小为1时，表明两传递函数的形状和幅值完全一致。

灵敏度分析方法包括微分法和有限差分法。传递函数相关系数的灵敏度表示结构的某一部分参数改变对相关系数的影响，即给定的状态参数下，相关系数对于状态参数的偏导数

为了使有限元模型与实际结构的动态特性更加接近，传递函数灵敏度的有限元模型修正方法为

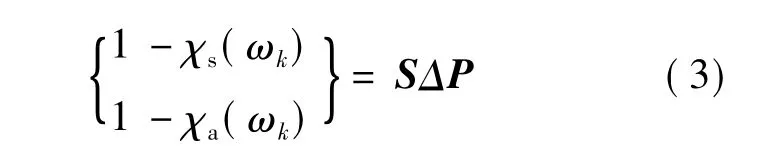
将频响函数相关系数写成实部和虚部形式，灵敏度矩阵［S］为

依赖预测和测量的传递函数的相关系数，有限元模型修正计算是一种迭代的过程，收敛条件为:若则计算停止。式中常数k的取值范围根据模型的复杂程度确定，一般取0.5～1.0之间。

2 圆柱壳体有限元模型的修正

圆柱壳体直径2.7 m，长度4 m，壁厚10 mm，外壳均布环肋加强，均分为20个肋位，舱壁采用加筋结构加强，内含加筋平台结构和基座结构，结构示意于图1。基座结构安装在13～17#肋位处底部，长745 mm、宽200 mm、高300 mm，面板厚9 mm、5块肘板和1块腹板厚5 mm，材料为碳钢，圆柱壳体采用空气弹簧支撑，垂向固有频率为3 Hz，远低于加筋圆柱壳体的结构振动模态(第1阶固有频率为111 Hz)，近似认为处于自由～自由状态。

图1 圆柱壳体结构示意

建立圆柱壳体结构的有限元模型见图2。

其中圆柱壳体、基座、平台及舱壁结构均用SHELL壳单元，加强筋和加强肋骨使用BEAM单元。为使有限元离散结构准确地描述圆柱壳体结构中应力波的传播，一个波长内至少应有5个节点(4个单元)，单元的长度约80 mm(1 700 Hz)。模型共含11 214个单元，7 978个节点。

图2 圆柱壳体结构的有限元模型

圆柱壳体模型是由众多的钢板焊接而成，对于不同的焊接方法、工艺和焊接材料，焊接后焊缝的刚度和厚度与原来钢板不同，因而在有限元建模时需要依据实测结果对有限元模型参数进行修正，以减少计算误差。为完善圆柱壳体及基座结构的有限元模型，开展圆柱壳体模型的振动模态和振动传递特性实验［10］。以基座面板至壳体上若干个代表性位置的传递函数为目标函数，先以材料的弹性模量、密度参数为变量，再以结构阻尼参数为变量，通过对变量迭代的方法修正有限元模型，在800 Hz低频范围内，取计算停止条件的常数k=0．7。

对有限元模型修正后，圆柱壳体结构的振动模态结果对比见表1。

表1 圆柱壳体结构的振动模态结果

圆柱壳体结构前10阶固有频率的计算误差小于8%，振型(m，n)代表圆柱壳体表面沿着轴向、周向的变形。实验测试得到的圆柱壳体振动模态阶次比有限元模态计算结果少，主要是由于实验时测点数目较少、受频率步长影响、或部分密集模态重合等因素，造成个别振动模态参数没有被有效识别出来。在基座面板上施加模拟激励，计算或测试圆柱壳体上不同位置的加速度响应，从而得到基座至壳体表面的传递函数。基座至壳体0#、6#肋位顶部位置的传递函数有限元仿真与实验结果对比见图3。在0～800 Hz低频率范围内，计算与实验结果吻合较好，传递函数峰值较为接近，趋势基本一致，平均幅值误差在3 dB以内;随着振动频率的增加，传递函数幅值的总体趋势接近，但误差增加，在800～2 000 Hz频率范围内，传递函数平均幅值的误差为6.8和14.2 dB。

图3 基座至壳体表面的传递函数

结果表明，修正后的圆柱壳体有限元模型，在800 Hz低频范围内能较好地反映实际结构的动态特性;在更高频率的计算结果中只能定性地反映振动特性的变化趋势。

3 基座板厚对传递函数的灵敏度

基座面板、腹板和肘板厚度对传递到壳体表面的传递函数灵敏度，反映了基座板厚对振动传递影响的灵敏程度。板厚对传递函数灵敏度＜0，说明板厚增加，传递函数下降，传递到壳体上的振动减少;传递函数灵敏度的幅值越小，说明板厚增加越有利于抑制基座结构的振动传递。

基座面板、腹板和肘板厚度对壳体上0#肋位顶部位置的传递函数灵敏度见图4。在800 Hz低频范围内，传递函数灵敏度的幅值较小，说明基座板厚对振动传递的影响较小;在800～2 000 Hz频率范围，少数频率处的传递函数灵敏度＞0，多数频率处的传递函数灵敏度＜0。基座的传递函数灵敏度幅值波动较大，说明基座板厚对振动传递函数的影响较大。在基座面板、腹板和肘板中，腹板厚度的传递函数灵敏度函数最小，面板厚度的灵敏度函数最大，即改变基座面板的厚度，对控制振动传递的效果更明显，在多数频率下，增加基座面板的厚度可以减小壳体表面振动的传递。

图4 板厚对壳体上的传递函数灵敏度

4 基座板厚对振动传递的影响

基座面板厚度对壳体上振动传递函数的影响见图5。

图5 面板厚度对振动传递函数的影响

当面板的厚度从4 mm增加到12 mm时，在800 Hz低频率范围，振动传递函数的平均值降低约4 dB;在800～2 000 Hz中高频率，面板厚度对振动传递函数有较大影响，振动传递函数在部分频率下的起伏波动量约10 dB，平均值降低6 dB。振动传递函数的变化趋势与传递函数灵敏度分析结果一致。在圆柱壳体上不同位置，基座面板厚度对振动传递函数的影响规律相近。这是由于仅基座面板的厚度参数，并不改变在低频时主要受圆柱壳体低阶次振动模态影响的振动传递特性，在中高频段，基座面板厚度的增加导致基座阻抗提高，从而减少基座的振动传递。

图6为基座不同板厚比(计算板厚与设计板厚的比值)时壳体上的振动传递函数。板厚比从0.4增加到2.4时，在800 Hz低频率范围，振动传递函数的平均值降低约6 dB;在800～2 000 Hz中高频率范围，板厚比对振动传递函数有较大影响，振动传递函数在部分频率下的起伏波动量约10～20 dB，平均值降低17 dB;板厚比从1.0增加到1.6时，中高频传递函数的平均值降低约5 dB，在板厚比增加到1.6时，传递函数平均值下降的趋势减缓。

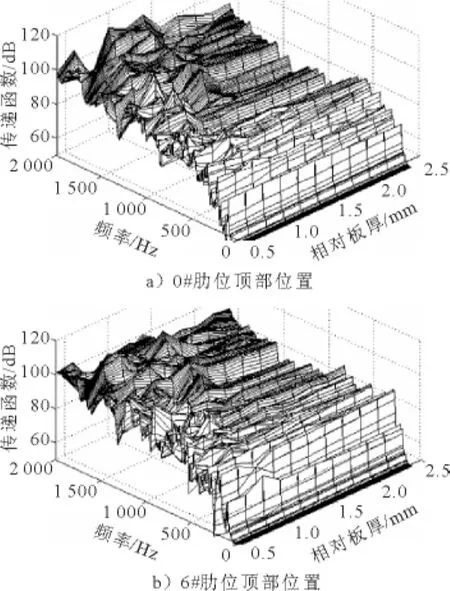
图6 基座板厚比对振动传递函数的影响

5 结论

采用传递函数灵敏度分析的有限元模型修正方法，可使建立的有限元模型较好地反映实际结构的动态特性。修正后的圆柱壳体有限元模型，前10阶固有频率的计算误差小于8%，传递函数幅值在800 Hz低频率范围较为接近实验结果，平均幅值误差在3 dB以内，传递函数幅值在中高频的总体趋势与实验结果基本一致。

轴向、周向的变形，一些难以确定的参数采取度圆柱壳体的中高频传递函数对结构参数的传递函数灵敏度分析，可用于指导结构的声学设计。整体改变基座的板厚，对基座结构振动模态的影响较大，基座阻抗在中高频明显增加，基座至圆柱壳体的中高频振动传递明显下降;但板厚增加到一定程度时，振动传递的下降幅度减缓。这对基座结构的声学设计具有参考价值。

［1］邓江华，刘献栋，李兴虎，等.车身阻尼层结构的声灵敏度分析及优化［J］.噪声与振动控制，2009(1):54-57.

［2］赵群，张义民，赵晋芳.振动传递路径的功率流传递度灵敏度分析［J］.振动与冲击，2009，28(7):183-186.

［3］JANSEN E L.A perturbation method for nonlinear vibrations of imperfect structures:application to cylindrical shell vibrations［J］.International Journal of Solids and Structures，2008，45:1124-1145.

［4］刘小勇，盛美萍，行晓亮，等.双层圆柱壳噪声预报及统计能量参数灵敏度分析［J］.振动与冲击，2007，26 (7):50-53

［5］徐张明，沈荣瀛，华宏星.基于频响函数相关性的灵敏度分析的有限元模型修正［J］.机械强度，2003，25 (12):5-8.

［6］温华兵，王国治.基于频响函数相关系数灵敏度的浮筏舱段有限元模型修正［J］.江苏科技大学学报:自然科学版，2005，19(6):75-79.

［7］WANG Ouozhi，ZHEN Xuegui.Improvement of dynamic property ofraft structure in vibration isolation system through sensitivity analysis［C］//Proceedings of the 4th Intemational Conference 011 Advances in Steel Structures，13.15 June.Shanghai，Elsevier Ltd，Oxford，UK，2005:1737-1742.

［8］温华兵，王国治.基于频响函数灵敏度分析的鱼雷模型有限元模型修正［J］.鱼雷技术，2006，14(3):10-14

［9］彭伟才，何锃.基于统计能量模型的辐射声功率灵敏度分析［J］.中国舰船研究，2009，4(6):11-14.

［10］温华兵，左言言，夏兆旺，等.加筋圆柱壳体支撑结构振动传递特性试验研究［J］.船舶力学，2013，17 (7):785-792.

Effect of Supporting Structure Plates Thickness on the Vibration Transmission Characteristics of a Cylinder Pressure Hull

WEN Hua-bing，LIU Lin-bo，WU Chen-hui
(Institute of Vibration and Noise，Jiangsu University of Science and Technology，Zhenjiang Jiangsu 212003，China)

The FE model of cylinder pressure hull and platform structure is built and the transfer function correlation coefficient of the experiment and the FE model is given to analyze the sensitivity of the transfer function correlation coefficient as well as to modify the FE model.As the results，the calculation deviation of the first 10 nature frequencies is less than 8%and the transfer function amplitude deviation of the calculation and experiment results is less than 3 dB under the frequency of 800 Hz. Based on the transfer function correlation coefficient sensitivity analysis，the effects of the panel thickness of supporting structure on vibration transfer are investigated.

supporting structure;transfer function;correlation coefficient;sensitivity analysis;modal;FEM

U661.4

A

1671-7953(2015)02-0006-05

10.3963/j.issn.1671-7953.2015.02.002

2014-05-19

修回日期:2014-11-16

国防基础科研项目(2010CH001G)

温华兵(1977-)，男，博士，副教授

研究方向:振动噪声控制

E-mail:wen-huabing@163.com