复合材料层合板的双Hopf分叉分析*
2015-05-24周艳张伟
周艳 张伟
(北京工业大学机械工程与应用电子技术学院,北京 100124)
引言
复合材料层合板振动与稳定性的研究始于上世纪八十年代,随后许多学者开始关注层合板的非线性振动响应问题.Nayfeh等人[1]利用实验方法研究了在简谐激励下复合材料层合板的非线性振动问题.Abe等人[2]利用多尺度法研究了简谐激励作用下矩形层合薄板的两模态非线性响应.Chen等人[3]研究了通常情况下在初始不均匀应力作用下的层合板大振幅非线性动力学方程.Ye等人[4,5]研究了正交对称铺设及反对称铺设的复合材料层合板在参数激励作用下的非线性振动和混沌运动.Zhang等人[6]研究了复合材料层合板在1∶1内共振情况下的周期和混沌运动.Guo等人[7]研究了角铺设复合材料层合板的非线性动力学响应.
首先引入了复合材料层合板的非线性动力学方程,利用多尺度法得到系统在直角坐标和极坐标形式下的平均方程,利用高维非线性系统的Hopf分叉定理,研究了复合材料层合板在主参数共振-1∶1内共振下的双Hopf分叉.数值模拟给出了系统在一定条件下存在不同形式的周期运动.
1 复合材料层合板的平均方程
以飞机机翼的颤振为工程背景,把机翼的局部简化为如图1所示的力学模型,它是一块具有纤维增强正交各向异性对称结构的复合材料层合薄板,此薄板四边简支并且同时受到横向载荷与x方向的面内载荷共同作用.薄板的长、宽、高分别为a,b和nh,直角坐标系oxyz位于层合板的对称平面内,z轴向下,设薄板内任一点沿x,y和z方向的位移分别为u,v和w,沿x方向作用的面内载荷为p=p0-p1cosΩ2t,横向载荷为 F=F0-F1cosΩ1t.
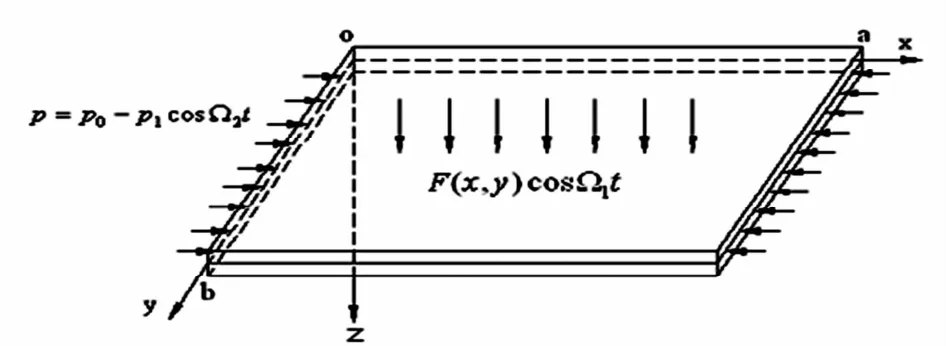
图1 横向与面内载荷作用下的层合薄板模型Fig.1 Themodle of the thin plate subjected to its plane and transverse excitation
我们得到如下形式的二自由度非线性动力学方程[8],
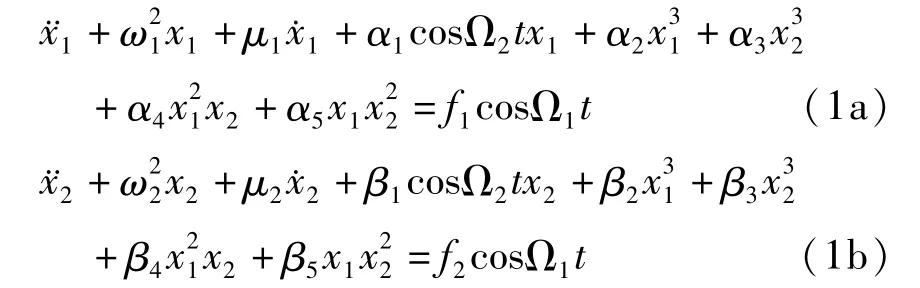
假设系统(1)是一个弱非线性系统,我们引入小扰动项ε,得到如下方程,

研究复合材料层合板在主参数共振—1∶1内共振情况下的双Hopf分叉特性,共振关系如下
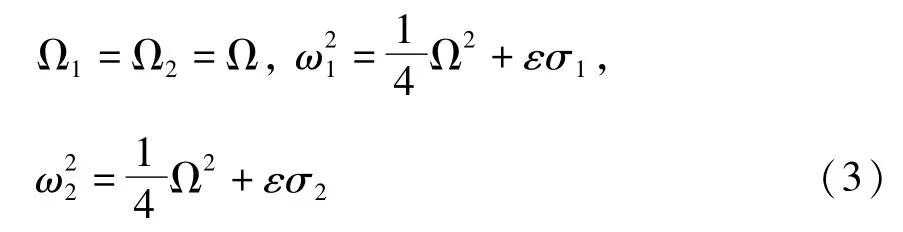
其中ω1和ω2是相应线性系统的第一阶和第二阶固有频率,为了计算方便,设Ω=2.
利用多尺法得到复合材料层合板直角坐标形式的平均方程为
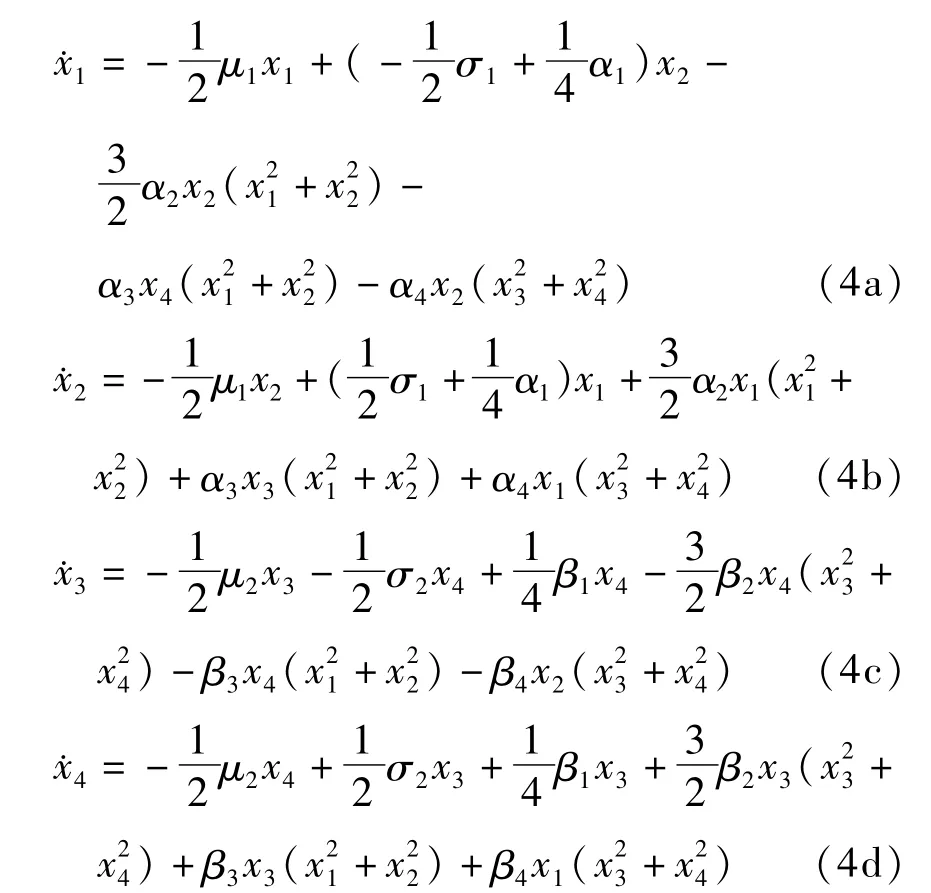
系统(2)极坐标形式的平均方程可以表示为
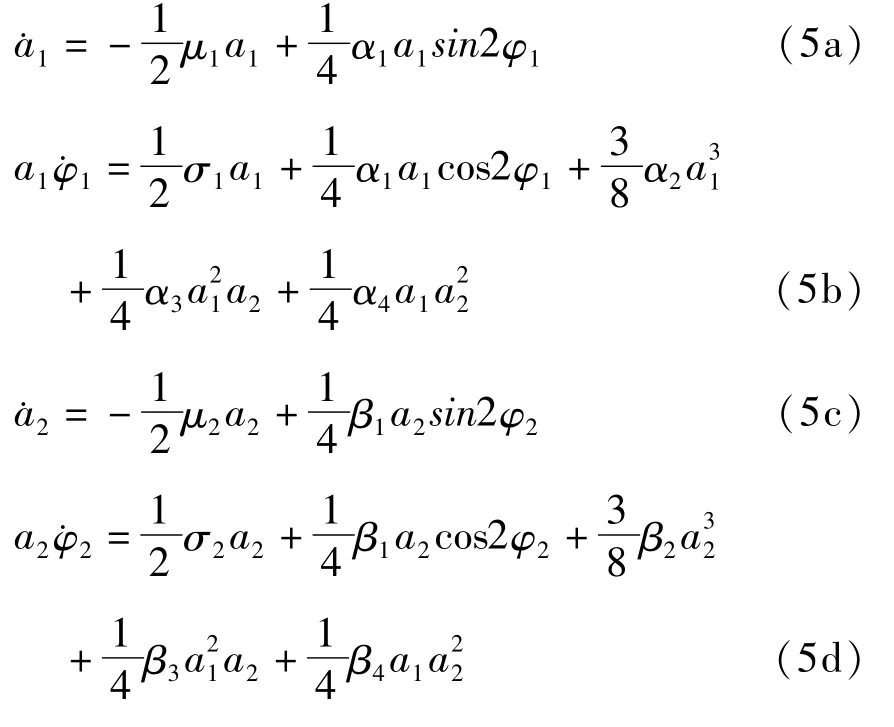
2 复合材料层合板Hopf分叉分析
在以下分析中,我们主要考虑复合材料层合板可能存在的各种平衡点分叉以及平衡点附近可能存在的周期解.方程(4)在零解处的Jacobi矩阵为
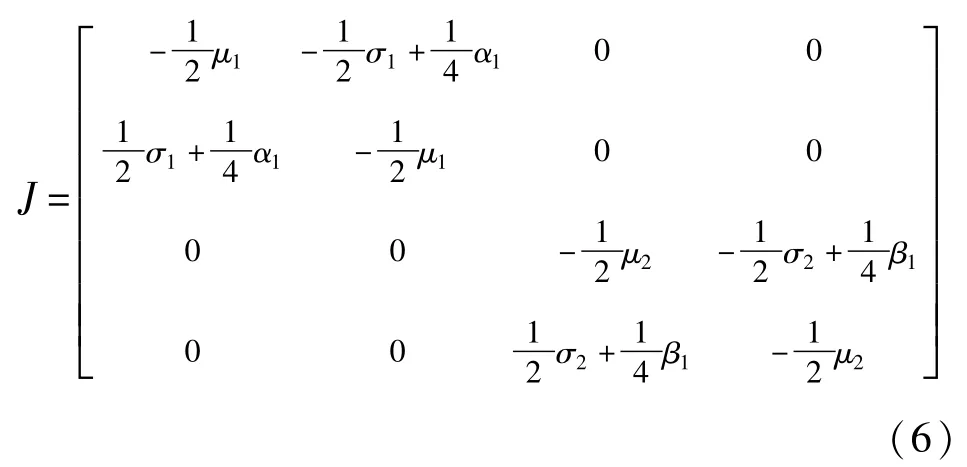
特征方程为
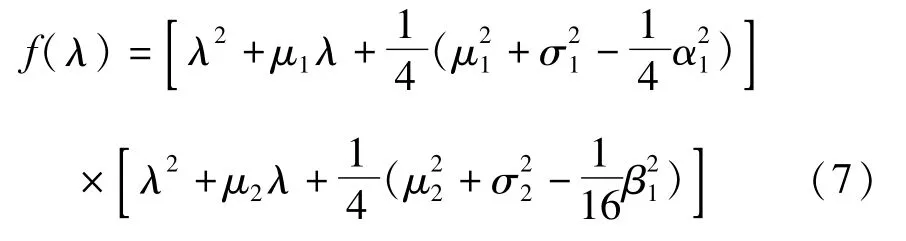
我们得到当时,方程(4)零解的稳定性临界线为
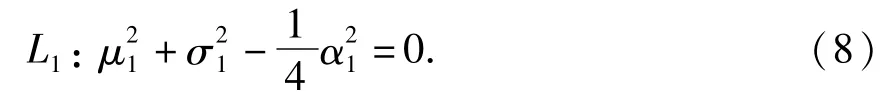
由奇异性理论[9]可知方程(4)的零解在临界线L1上发生静态分叉,系统(2)产生第一类型的周期解(x1,x2,0,0),可以表示为

当时,系统(4)零解的稳定性临界线为
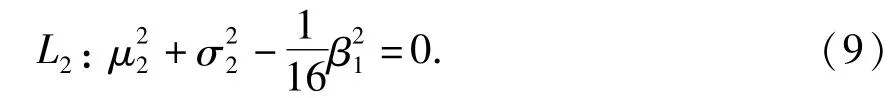
根据方程(4)在(x1,x2,0,0)处的 Jacobi矩阵和特征方程可知,当时,第一类型周期解的稳定性临界线为

当μ2>0时,系统(4)第一类型周期解的稳定性临界线为
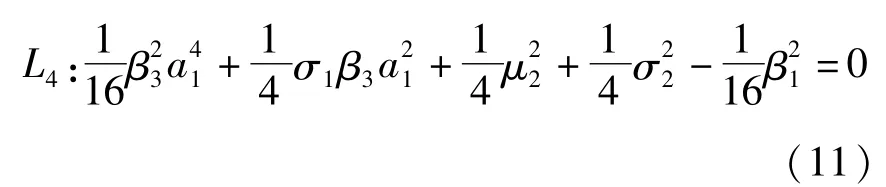
由奇异性理论[9]可知系统(4)的零解在临界线L2上同样发生静态分叉,系统(2)产生第二类型周期解,表示如下
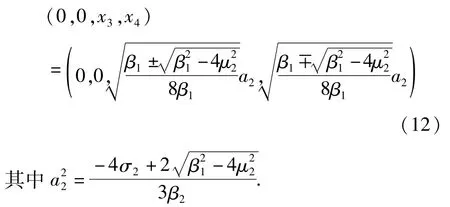
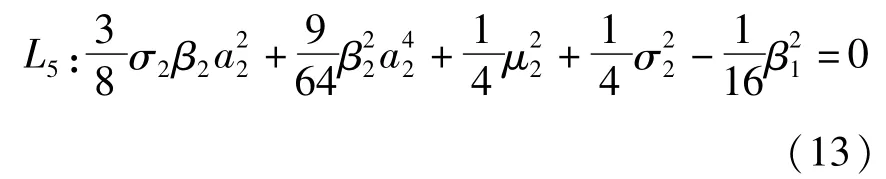
方程(4)第二类型周期解在临界线L5上将发生Hopf分叉而失稳,系统(2)的频率为和 ω4,其中 ω4是系统在(0,0,x3,x4)处产生的Hopf分叉频率,即
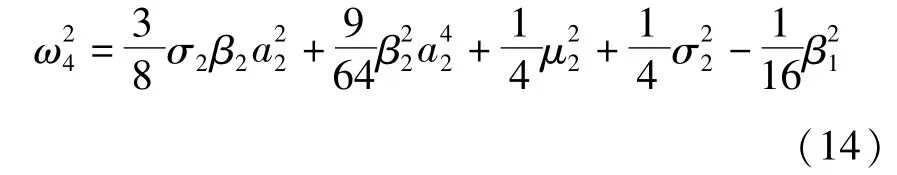
当μ1>0时,可得方程(4)的第二类型周期解的稳定性临界线为

3 数值模拟
利用数值模拟方法对复合材料层合板在主参数共振-1∶1内共振情况下的非线性动力学行为进行研究.利用Matlab程序对系统(4)进行数值模拟.分叉图2将平衡点附近邻域分为不同的区域,分别对应复合材料层合板不同的振动形式.图3至图5分别表示复合材料层合板不同形态的非线性振动特性.在以下各图中,图(a)和(b)分别是平面(x1,x2)和(x3,x4)上的二维相图,图(c)和(d)分别为平面(t,x1)和(t,x3)上的波形图.复合材料层合板的阻尼系数分别为 μ1=0.18和 μ2=0.36,其它参数和初值分别为 σ1=0.16,σ2=-0.41,α1=1.5,α2=0.4,α3=0.7,α4=0.3,β1=0.6,β2=0.2,β3=0.25,β4=0.69,x10=0.18,x20=0.43,x30=0.19,x40=0.42.

图2 复合材料层合板的局部分叉图Fig.2 The local bifurcation diagram ofcomposite laminated thin plate
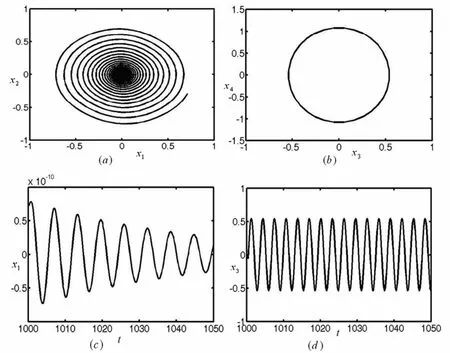
图3 复合材料层合板的第一类型周期运动Fig.3 The frist type of periodic motion of composite laminated thin plate

图4 复合材料层合板的第二类型周期运动Fig.4 The second type of periodic motion of composite laminated thin plate
4 结论
本文研究了受面内激励和横向激励联合作用下复合材料层合板的双Hopf分叉.利用Hopf分叉定理给出了系统平衡解在参数空间小邻域内发生的各种分叉现象,以及在主参数共振-1∶1内共振情况下发生双Hopf分叉的必要条件.数值模拟验证了理论分析的正确性.
1 Oh K,Nayfeh A H.Nonlinear resonances in cantilever composite plates.International Journal of Nonlinear Mechanics,1996,11(2):143~169
2 Abe A,Kobayashi Y.Three-mode response of simply supported,rectangular laminated plates.International Journal Series-Mechanical Systems Machine Elements and Manufacturing,1988,41(1):51~59
3 Chen C S,ChengW S,Chien R D,Dong J L.Large amplitude vibration of an initially stressed cross ply laminated plates.Applied Acoustics,2002,63(9):939~956
4 Ye M,Lu J,Ding Q,Zhang W.Nonlinear dynamics of a parametrically excited rectangular symmetric cross-ply laminated composite plate.Acta Mechanica Sinica,2004,37:64~71
5 Ye M,Sun Y,Zhang W,Zhan X P,Ding Q.Nonlinear oscillations and chaotic dynamics of an antisymmetric cross-ply laminated composite rectangular thin plate under parametric excition.Journal of Sound and Vibration,2005,287(4-5):723~758
6 Zhang W,Guo X Y,Lai S K.Research on periodic and chaotic oscillations of composite laminated plateswith oneto-one internal resonance.International Journal of Nonlinear Sciencesand Numerical Simulation,2009,10(11-12):1567~1583
7 Guo X Y,ZhangW,Yao M H.Nonlinear dynamics of angle-ply composite laminated thin plate with third-order shear deformation.Science in China Series E:Technological Sciences,2010,53(3):612~622
8 郭翔鹰.复合材料层合板的非线性动力学研究[硕士学位论文].北京:北京工业大学工学,2007(Guo X Y.The nonlinear dynamics research of composite laminated plates[Master Thesis].Beijing:Beijing University of Technology,2007(in Chinese))
9 Golubisky M,Schaeffer D G.Singularities and groups in bifurcation theory I.New York:Applied Mathematical Sciences,1985
