地震作用下考虑地基土层构成的高耸式结构物动力有限元分析
2015-05-24徐宾宾朱耀庭寇晓强郭玉彬
徐宾宾,朱耀庭,寇晓强,郭玉彬
(1.中交天津港湾工程研究院有限公司,天津 300222;2.港口岩土工程技术交通行业重点试验室,天津 300222;3.天津市港口岩土工程技术重点试验室,天津 300222)
地震作用下考虑地基土层构成的高耸式结构物动力有限元分析
徐宾宾1,2,3,朱耀庭1,2,3,寇晓强1,2,3,郭玉彬1,2,3
(1.中交天津港湾工程研究院有限公司,天津 300222;2.港口岩土工程技术交通行业重点试验室,天津 300222;3.天津市港口岩土工程技术重点试验室,天津 300222)
本文利用基于有效应力原理的有限元程序,计算了埋立在软弱成层地基上的高耸式结构物地震响应,重点考虑成层地基的土层构成对结构物地震稳定性的影响。结果表明:(1)地表土体为松散的冲填砂时,地震中产生砂土液化,极大的降低了地表承载力,高耸式结构物的埋深应适当增加;(2)地表土体为软弱的冲积黏土时,地震中并未产生液化破坏,但由于地表黏土层放大了地震波振幅,结构物摇晃剧烈,应着重验算结构物自身的抗弯刚度;(3)地表同为易液化的冲填砂、结构物埋深足够大时,还应考虑易液化层厚度,厚度较大的易液化层能够有效的减弱地表处地震波振幅,降低结构物的倾覆风险。
高耸式结构物;有效应力原理;有限元;地基土层构成;地震稳定性
1 研究背景
砂土液化是地震造成的巨大危害之一。现行的液化判断标准通常采用FL/PL法[1],虽然此法概念明确、应用方便,但其并未考虑地基中的各层土质,因此并不是一种准确的液化判别方法。Nakai等[2]统计了东日本大地震中采用FL/PL法预测共计112处砂土液化与否的情况,虽然FL/PL法预测的24处非液化地点在地震中并未液化,但在预测的88处有液化危险的却有35处并未液化。因此,越来越多的学者倾向于利用基于有效应力法的有限单元法分析地震中的砂土液化及结构物响应[3-4]。另外随着经济的快速发展,软弱地基上采用高耸式结构物的工程越来越多,精确计算其地震响应及地震稳定性越来越重要。目前在计算高耸式结构物的地震响应时,分析重点往往放在结构物本身的地震响应[5-6],忽略了支撑结构物的地基类型及地基构成,造成了预测的不准确或是不完整。本文利用基于有效应力原理的有限元程序,考虑支撑高耸式结构物软弱地基的土层构成,分析结构物的地震响应和地震稳定性。
2 计算条件
2.1网格划分及边界条件地基计算模型采用平面应变条件,如图1所示,由上至下分为4层。地基表面为大气压边界,考虑到地基底层土体渗透性较低以及地基长度足够大,底面和两个侧面为不排水边界。另外,为了施加地震荷载,分别在两个侧面施加周期性边界条件,地基底部为黏性边界[7-8]。
2.2地层构成及土性参数考虑软弱地基的特点,表层土体采用具有代表性的冲填砂或冲积黏土,表层以下分别为冲积砂、洪积砂和泥岩。按地表土体类型地基又可分为A、B、C三类,如图2所示,A类地基从上至下有冲填砂层、冲积砂层、洪积砂层和泥岩层;B类地基从上至下有冲积黏土层、洪积砂层和泥岩层;C类地基包括冲填砂层、冲积黏土层和泥岩层。
土体本构模型采用名古屋大学土质力学小组提出的上下负荷面剑桥模型[9],它可以利用结构性和超固结概念描述砂土的不同松散状态和密实程度以及黏土的不同扰动程度。表2给出了各层土体的上下负荷面剑桥模型参数,其中5个弹塑性参数与剑桥模型一致,分别为临界状态线斜率M、正常固结线在v-lnp′空间中的截距(p′=9.81 kPa时)、压缩指数λ~、膨胀指数κ~和泊松比ν;另外结构性退化指数a、超固结退化指数m、旋转硬化指数br为控制土体状态变化速度参数,具体可见文献[10]。需要注意的是,各种参数均通过拟合室内三轴试验和一维固结试验结果得到。

图1 网格划分以及边界条件

图2 地基土层构成和高耸式结构物埋深
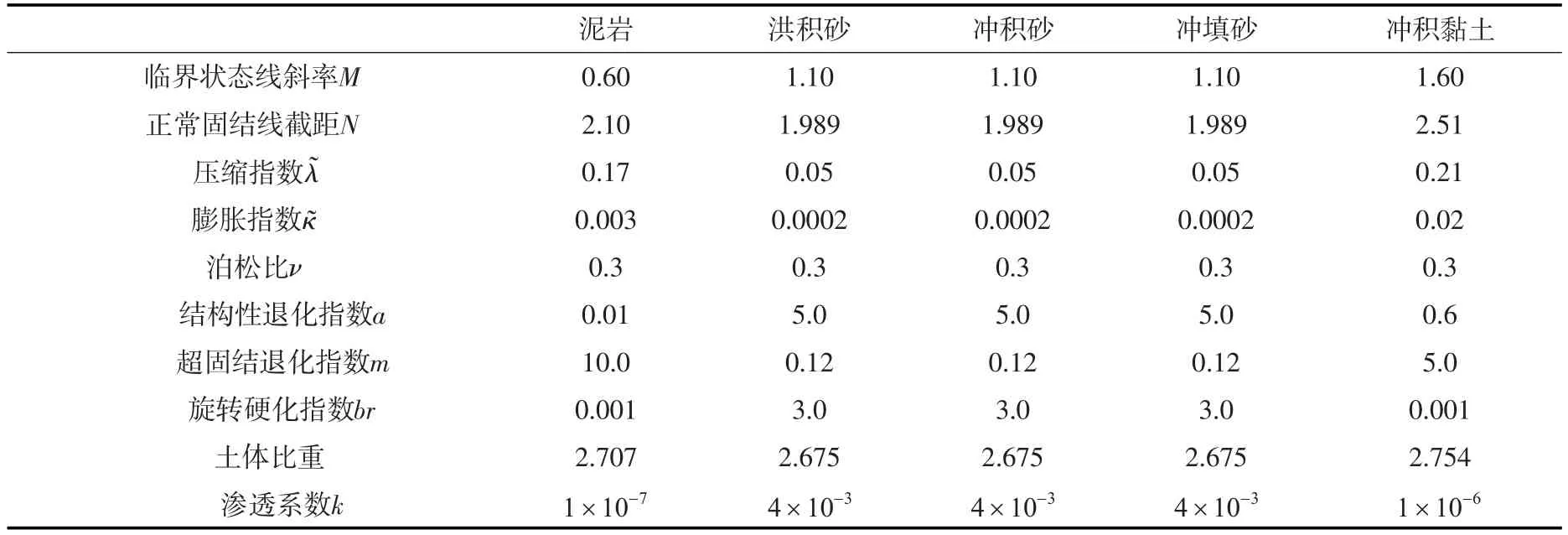
表1 地基中各层土体参数
2.3高耸式结构物参数高耸式结构物为轻量空心钢圆柱,高15 m,重2.4 kN,底部直径0.3 m,顶部直径0.14 m。结构物底部通过混凝土底座固定在地基上。考虑到计算采用平面应变条件,将三维的钢圆柱按照抗弯刚度相等原则换算为二维的“钢板墙”,钢圆柱及混凝土参数如表2所示。

表2 混凝土底座和空心钢圆柱的材料常数
2.4输入地震波计算中采用中日本防灾管理委员会预测的Tokai-Tonankai-Nankai地震波[11],如图3所示,最大加速度为300 gal,主震周期介于0.2~0.4 s,持续时长100 s。
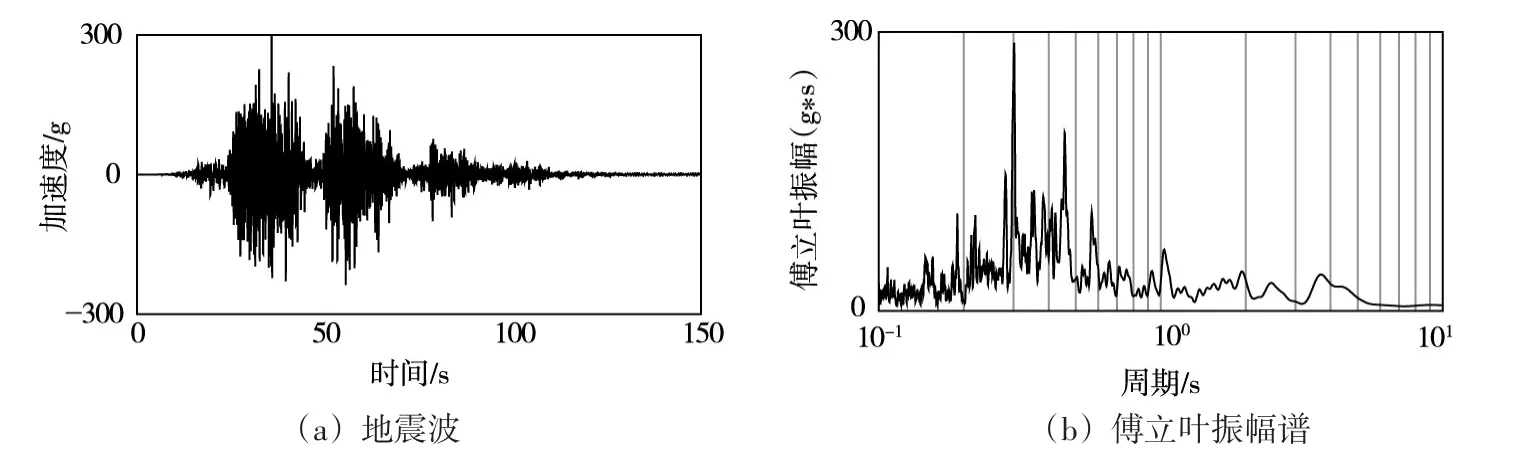
图3 地震波曲线及傅立叶振幅谱
3 计算结果及分析
为验证高耸式结构物的地震稳定性,计算方案如表3所示,考虑了结构物埋深、地表土体类型、地表易液化层厚度的影响。
3.1结构物埋深影响考虑结构物埋深影响时,采用A类地基且地表易液化层厚度均为12 m,结构物埋深分别取1 m、2 m,如表3中情况1和情况2所示。

表3 计算方案
为深入理解地基各层土体的地震响应,分别在各个地层中取土体单元并计算地震反应。图4中给出了各层土体地震中的有效应力路径变化,其中平均有效应力S=σ′-p′I,(σ′为有效应力张量)。可以看到,泥岩由于刚度大,地震中偏应力和平均有效应力几乎没有减小;洪积砂在地震中偏应力和平均有效应力均有所减小,但并未减小至零;而冲填砂和冲积砂由于其相对密实度较小,其偏应力和平均有效应力均接近于零,即通常所说的砂土液化。
图5给出了情况1和情况2中结构物顶部的水平位移和沉降比较。虽然地震中地表砂土液化、结构物左右晃动剧烈,情况1中由于埋深较大,地震后其水平位移随着超静孔隙水压力的消散,地基刚度的恢复而逐渐收敛;而情况2中由于埋深较小,结构物因地表砂土液化,承载力降低产生了较大的侧向倾斜,竖向沉降也随之变大。实际工程中,若高耸式结构物侧向倾斜较大,可能会引起其上附着的电线、信号发射器等损坏,影响正常使用。
图6给出了情况2中地震结束3 min后地基内的剪应变分布以及结构物的倾斜程度。可以看到剪应变主要分布于冲填砂和冲积砂层内,混凝土底座周围则因为土与结构的相互作用产生了较大的剪应变,而结构物也有较大的侧向位移。
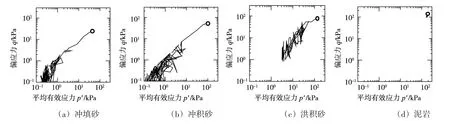
图4 地震中各层土体的有效应力路径变化
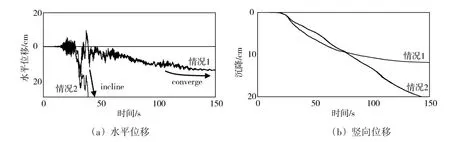
图5 情况1和情况2中结构物顶部的水平位移和竖向位移比较
地表土体类型影响 为了考虑地表土体类型对高耸式结构物地震稳定性的影响,分别计算表层土体为冲填砂和冲积黏土两种情况,结构物埋深均为1 m,如表3中情况2和情况3所示。
同样图7给出了地震中地表冲积黏土层的有效应力路径变化,与情况1中的洪积砂层类似,平均有效应力和偏应力均有所减小但并未接近于零,即并未产生液化破坏。
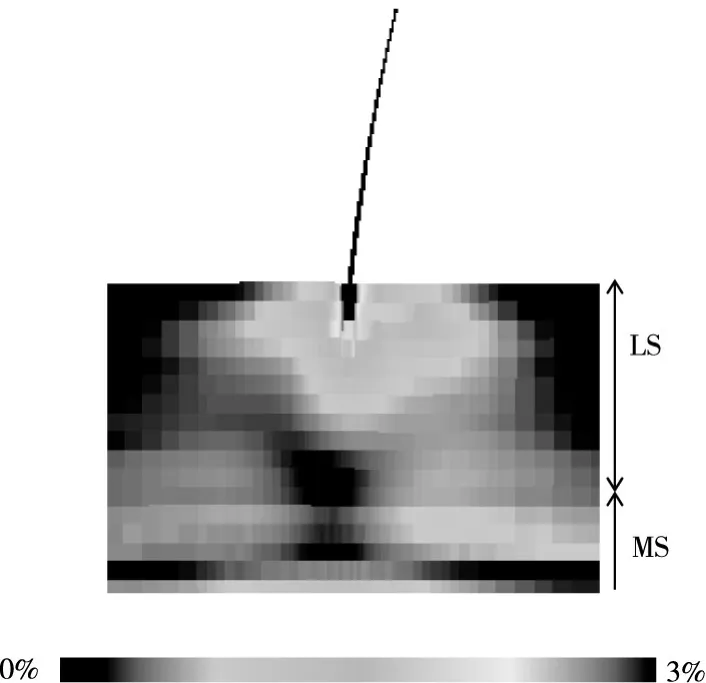
图6 情况2中地震结束3min后地基内的剪应变分布

图7 地震中冲积黏土层的有效应力路径变化
图8给出了情况2和情况3中结构物顶部的水平位移和竖向位移随时间变化情况。如前所述,情况2中由于地表冲填砂液化、地基承载力降低,结构物在地震中很快产生了较大的侧向位移;而情况3中虽然地震中结构物经历了剧烈的晃动,却并未产生较大的侧向倾斜,由此可知,虽然地表处地震波的振幅因冲积黏土层而被放大,结构物却因地基并未液化、地表仍有一定承载力而保持稳定性,此类地表时应着重验算结构物本身的抗弯刚度。
地表易液化层厚度影响 上述两节中已经比较了相同地基类型下结构物埋深和不同地表土体类型的影响,本节中将考虑相同埋深和相同地表类型时地表易液化层厚度的影响,如表3中情况4和情况5所示。
图9给出了情况1、情况4和情况5中结构物顶部的水平位移和竖向位移。由图9可知,虽然结构物埋深同为2m,且地表同为易液化的冲填砂,结构物的地震稳定性却相差极大。由图10可知,情况4中地表易液化层较厚,地震波在穿过该层时地震波振幅减小、有较大衰减;而情况5中地表易液化层较薄,地震波穿过该层时衰减较小,致使结构物很快产生了较大的侧向倾斜。

图8 情况2和情况3中结构物顶部的水平位移和竖向位移比较

图9 情况1、情况4和情况5中结构物顶部的水平位移和竖向位移比较
4 结论
本文通过基于有效应力原理的有限元计算,分析了在不同埋深、地表土体类型以及地表易液化层厚度条件下高耸式结构物的地震稳定性,得到如下结论:(1)地表为易液化的松散砂土层时,高耸式结构物的埋深应适当增加,防止因地震中砂土液化、地表承载力降低而产生较大的侧向倾斜;(2)地表土体为冲积黏土时,地震波在地表处被放大,地震波振幅变大,结构物摇晃剧烈,此时应着重验算结构物本身的抗弯刚度;(3)地表土体为易液化的松散砂土层时,地震波在通过地表砂土层时被衰减,地震波振幅减小。当易液化层厚度较大时,地震波衰减幅度也较大,结构物侧向倾斜较小;而当易液化层厚度较小时,地震波衰减程度较小,加之地表砂层液化而导致承载力降低,结构物很快失去稳定性;(4)对高耸式结构物进行地震稳定性分析时,须根据地质勘察资料,充分考虑地基土层的构成、地表土体类型以及地表易液化层厚度的影响,以提高计算和预测的准确性。
[1] Iwasaki T,Arakawa T,Tokida K.Simplified procedures for assessing soil liquefaction during earthquakes[J]. Soil Dynamics and Earthquake Engineering,Southampton,1984,3(1):925-939.
[2] Nakai K,Noda T.A means for assessing the seismic stability of a temporary structure sited on soft ground and pre⁃venting its collapse[J].Japanese Geotechnical Journal,2010,5(3):499-510.
[3] 郝鹏,刘云贺,刘哲,等.隧道围岩结构地震动稳定性分析的动力有限元强度折减法[J].水利学报,2011,42(4):1241-1248.
[4] 陈灯红,戴上秋,彭刚.坝-基动力相互作用的高阶时域模型[J].水利学报,2014,45(5):547-556.
[5] 马人乐,牟宗磊,何敏娟,等.钢结构电视塔塔楼在竖向地震作用下的反应分析[J].特种结构,1998,15(2):42-45.
[6] 刘红梅,金江,王海霞.塔式结构地震波响应仿真分析[J].南通大学学报:自然科学版,2006,5(4):25-28.
[7] Lysmer J,Kuhlemeyer R L.Finite dynamic model for infinite media[J].ASCE,1969,95(4):859-877.
[8] Noda T,Asaoka A,Nakano M.Soil-water coupled finite deformation analysis based on a rate-type equation of motion incorporating the SYS Cam-clay model[J].Soils and Foundations,2008,48(6):771-790.
[9] Asaoka A,Noda T,Yamada E,et al.An elasto-plastic description of two distinct volume change mechanisms of soils[J].Soils and Foundations,2002,42(5):47-57.
[10] Asaoka A,Nakano M,Noda T.Superloading yield surface concept for highly structured soil behavior[J].Soils and Foundations,2000,40(2):99-110.
[11] Center Disaster Mamagmemt Councol.Research report about Tokai-Tonankai-Nankai earthquake[R].2003:18-20.
Dynamic seismic stability analysis of erect structure considering soil stratigraphic
XU Binbin1,2,3,ZHU Yaoting1,2,3,KOU Xiaoqiang1,2,3,GUO Yubin1,2,3
(1.CCCC Tianjin Port Engineering Institute Co.Ltd,Tianjin 300222,China;2.Key Laboratory of Port Geotechnical Engineering,Ministry of Communications,Tianjin 300222,China;3.Key Laboratory of Port Geotechnical Engineering of Tianji,Tianjin 300222,China)
The seismic response of erect structures mainly focuses on the response of the structure itself without considering the effect of soil profiles.In this paper,the seismic stability of erect structures built on the multi-layer ground is investigated based on the finite element method and the emphasis is put on the influence of soil stratigraphic on the seismic responses of the structure.The results show that:(1)when the surface ground is loose sand,liquefaction occurs in this layer,which results in the great de⁃crease of the bearing capacity,and the embedded depth of the structure should increase;(2)when the surface layer is weak clay,there is no liquefaction in this layer.However,the seismic wave is greatly am⁃plified during this layer and the structure oscillates greatly.Therefore,the stiffness of the structure should be verified carefully;(3)when the thickness of the liquefiable layer is small,the attenuation of the accel⁃eration in the liquefiable layer is small,so the stability of the structure above is significantly reduced.This means,even when the soil of the surface layer on which the structure is installed is the same,the stabili⁃ty of the structure during the earthquake varies greatly depending on the differences in the stratigraphic composition.
erect structure;effective stress principle;FEM;Soil stratigraphic;seismic stability
TU311.3
:Adoi:10.13244/j.cnki.jiwhr.2015.03.013
1672-3031(2015)03-0227-06
(责任编辑:李 琳)
2014-05-15
徐宾宾(1984-),男,河南焦作人,博士,工程师,主要从事软土地基处理及数值计算分析研究。
E-mail:xubinbin@tpei.com.cn
