基于方差-协方差组合预测的 中长期电力负荷预测研究
2015-05-23唐祥玲李思岑白朝元
唐祥玲 王 平 李思岑 白朝元
(西华大学电气信息学院,成都 610039)
电力负荷预测关系到如电力系统的规划和设计,电力系统经济、可靠和安全的运行、电力市场公平的交易等多个电力部门。所以,更精确地预测出电力负荷是很重要的。要精确科学地预测出未来某段时间的电力负荷,需要掌握并研究过去一定时间的电力负荷历史数据,而经济发展,社会变化,气象万千又影响着预测精度,因而找出一个好的预测方法至关重要。
电力负荷预测分为中长期和短期,目前国外研究出的成果比较成熟,而国内在技术上的发展明显滞后于经济的发展,在短期的电力负荷预测中的研究比较多,而中长期的研究比较少,所以对中长期电力负荷预测进行深入地研究是非常迫切的。
目前现有的负荷预测的方法基本分成三类:经典技术方法(如分产业产值单耗法、电力消费弹性系数法、负荷密度法、人均电量指标换算法、分类负荷预测法)、传统预测方法(回归预测法、时间序列预测法、趋势外推预测法等)、现代预测法(灰色预测法、神经网络法、混沌预测法、模糊预测法、专家系统法、优选组合预测法、小波分析法)。经典的技术方法在面临多重影响预测的不确定因素时预测困难,而且预测方法中大部分只适用于短期预测(如神经网络法、混沌预测法、小波分析法)。而其余的预测方法的必然适用范围不同并且精度也不同。怎样才能更精确地预测出中长期电力负荷呢?本文采用的组合预测法,将线性回归模型、二次多项式模型和灰色预测模型组合起来,能利用各预测方法的优点,顺应电力负荷指标繁多、变化各异的特点,预测出的结果大大提高了预测精度,为中长期电力负荷预测做出参考。
1 线性回归模型
回归分析法预测电力负荷目前技术相对其他方法更加成熟,过程简单,计算简便,特别是线性回归模型[1]。
假如自变量t和因变量y之间有线性关系,表示为

式中,变量x可是一般变量,也可是随机变量。变量y是随机变量,受变量x影响。c、b为待定系数,ε表示其他随机因素对y的影响总和,即随机误差, 服从正太分布N(0,δ2)。
对于很多个点数据,用xi代表自变量x的值,y i代表y的实际值,是yi的估计值,则有线性回归模型:

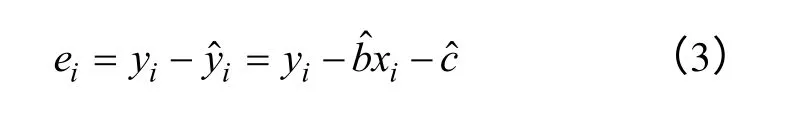
2 二次多项式模型
线性回归模型虽然简便,但是预测出的负荷精度较低,不适应变化较大的历史数据,现介绍的二次回归模型[2]相比线性回归更加适合于用电量被多样化和不确定性的因素影响的时候。
假如自变量x和因变量y之间有非线性关系,可以表示为
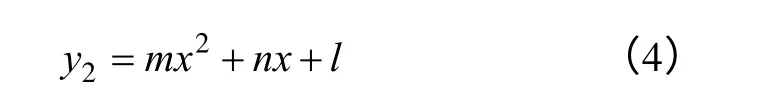
式中,m、n、l为待定系数,x表示时间,2y表示电量。
用最小二乘法的极小值原理,代数多项式拟合可计算出待定系数。
对于多项式
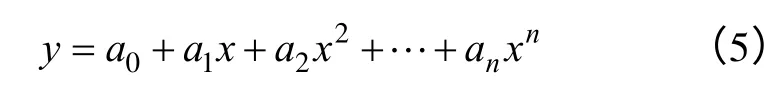
其最小二乘法的法方程为
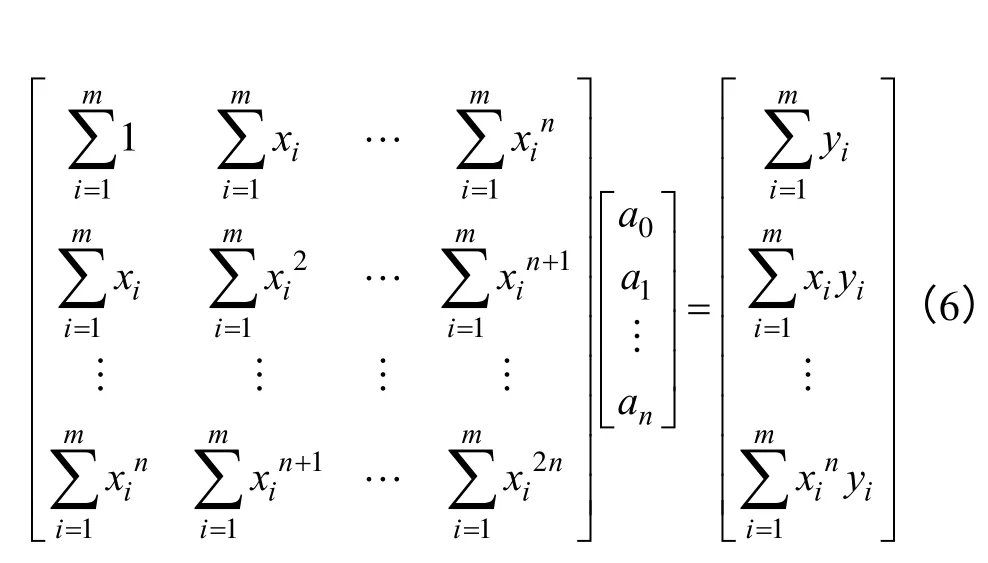
式中,n= 1,2,… ,m= 1,2,…。
3 灰色预测模型
灰色预测法能够考虑各种外在影响因素,负荷精度较高,对历史数据的要求较低,并且运算处理速度快,对预测结果能进行有效检验,这种预测方法在电力行业已得到普遍的应用。
灰色模型[3]中GM(1,1)模型是其中非常实用的一种,它的计算步骤是首先累加处理原始数据,再建立微分方程模型,求得拟合曲线,三是还原即可得到预测值。该模拟曲线上的数据符合指数规律,适用于预测具有单调性的指数序列。 假设用电量或者负荷的原始数据序列为
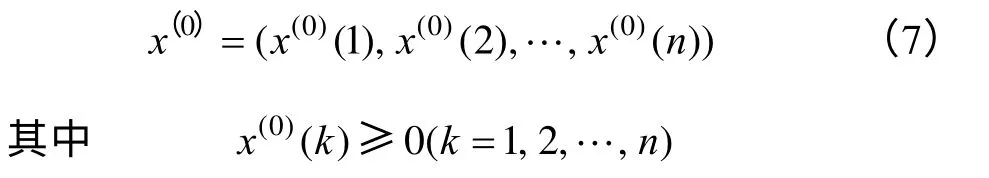
首先,累加处理原始序列,产生一个新的序列:
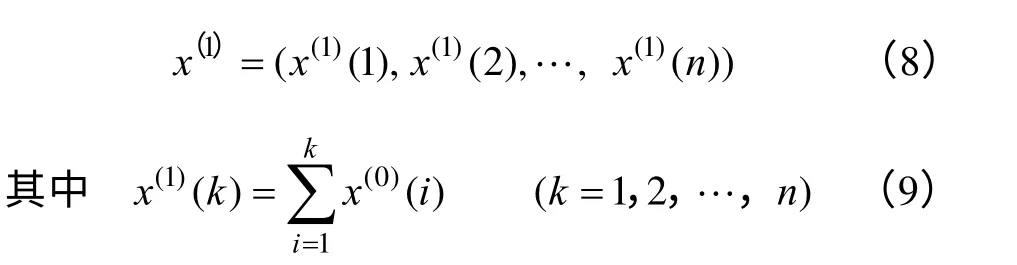
和原数列相比较生成的新数列是一个单调增长的曲线,如此便增强了原数列的平滑度,减小了原始数列的随机性,即增加了新数列的数据规律性。
x(1)(k)序列符合指数增长规律,因此需要建立关于x(1)序列的一阶微分方程模型:
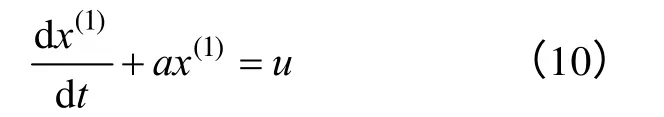
a,u为参数。记其中a,u的预测值分别为是则由最小二乘法求得参数Aˆ:
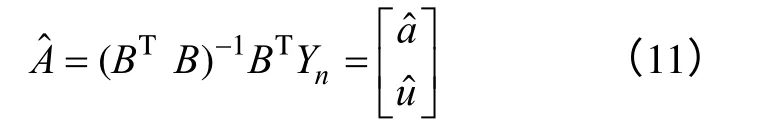
式中,B和Yn为已知量,为待定参数,由下面两式求得B和Yn。
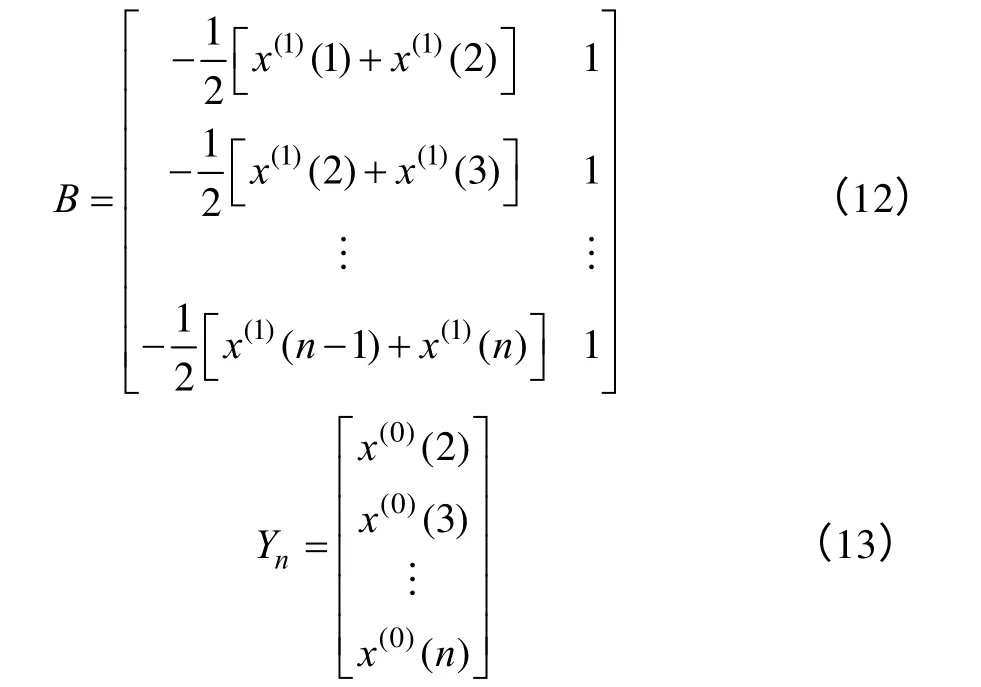
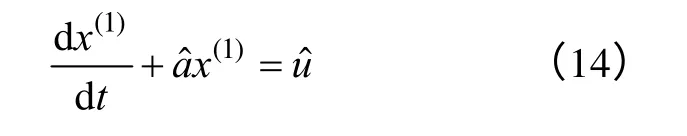
GM(1,1)的生成序列由式(14)离散化后便得到,其灰色模型(或称时间响应序列)为
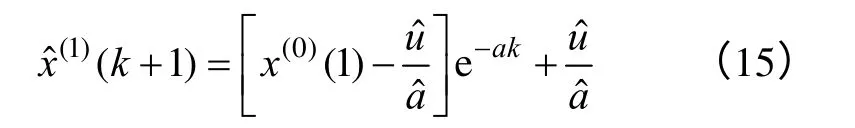
式中,k= 0,1,2,…。
最后,将式(15)累减还原之后,可以达到目的,求得灰色预测模型:
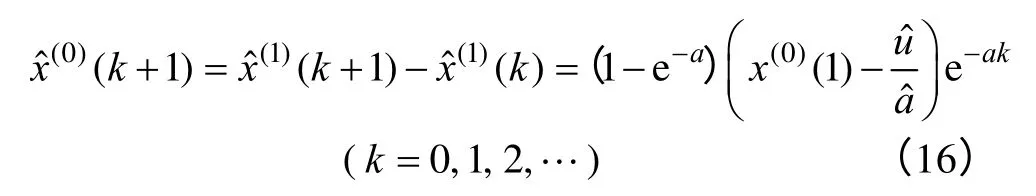
4 方差-协方差组合预测法
回归模型和二次多项式模型的计算简便,但相对的预测精度较低,外界影响下历史数据波动大的情况下精度更降几成。而灰色预测只有在原始数据具有良好的光滑性能时预测精度较高,因此构建组合预测模型可以综合各单一模型的优点,提高预测精度。方差-协方差组合预测[4]相对于其他组合预测法的优点是可以求得最佳的组合权系数,提高预测的稳定性和准确性。
设f1、f2、f3分别为三个模型的预测值,fc为加权平均的组合预测值,w1和w2、w3为相应的权系数,则:
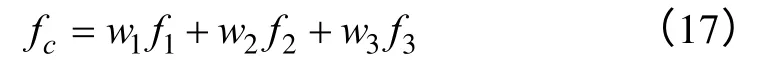
误差和其方差Var(ec)(fc也是无偏的)分别是:
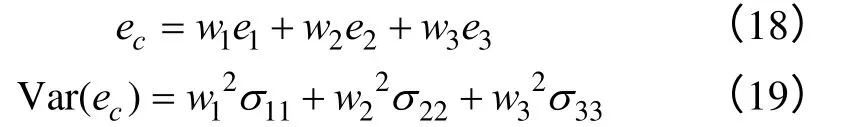
其中e1,e2、e3分别为三个预测模型的预测误差,组合预测的误差为ec,且w1+w2+w3= 1。σ11、σ22、σ33分别为三个预测模型的测误差方差。 求wi(i= 1,2,3)的极小值,可以引入拉格朗日乘子来求得。
三个预测方法的组合预测权系数分别为
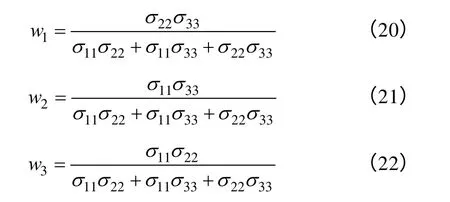
从式(20)中可以看出
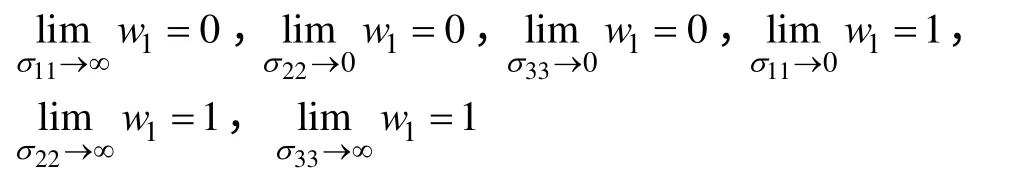
可得出结论:f1的权数值与该预测值的误差成反比。
5 应用及算例结果分析
根据某市2008—2013年每年的电力负荷数据,通过线性回归预测模型、二次多项式模型和灰色预测模型分别进行预测得出预测数据,并组合预测,结果如下。
5.1 线性回归模型
假设线性回归模型为y=c+bt
t为第几年的负荷,y为负荷量。
通过历史数据,用 Matlab 算出c= 1799.7,b= 291.5。
可得线性模型为y= 1799.7 + 291.5t
即可计算出预测负荷及误差,如表1所示。

表1
5.2 二次多项式模型
二次多项式模型为y2=mx2+nx+ l
由(6)式可得二次多项式的最小二乘法的方程计算式为

将表2数据代入(23)可得
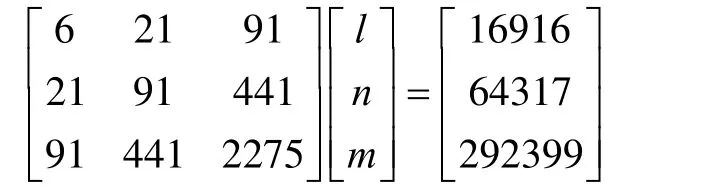
得出待定系数为m= 1.7,n= 280.3,l= 1812.8
由此可得到二次多项式为
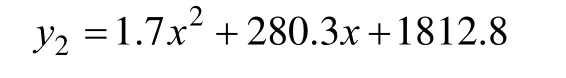
即可计算出预测负荷及误差,如表2所示。
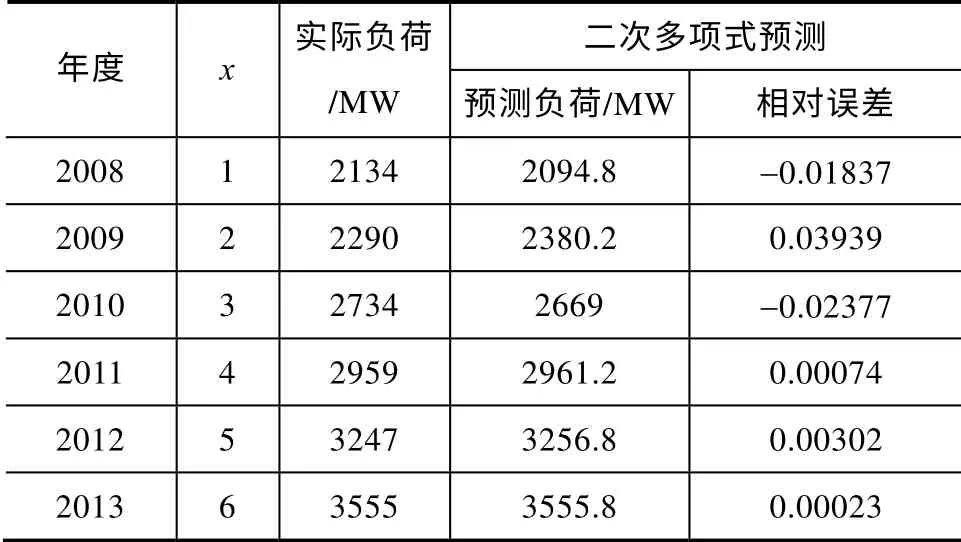
表2
5.3 灰色模型
直接用Matlab 计算出灰色预测模型的预测数据,见表3。
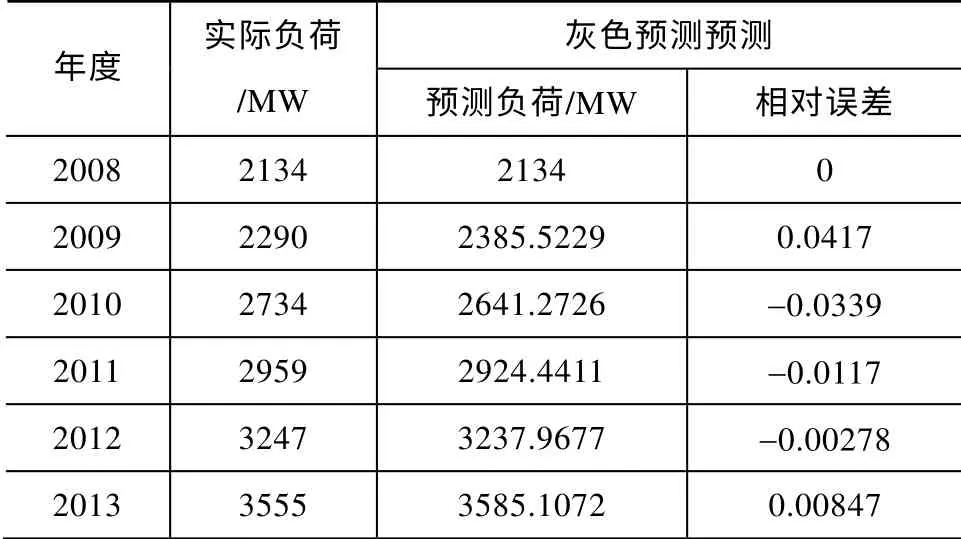
表3
5.4 组合预测模型
由各个模型数据,可计算出σ11= 2364.965,σ22= 2333.2,σ33= 3317.556。即可得w1= 0.3668,w2= 0.3718,w3= 0.2614,那么预测结果如表4所示 。
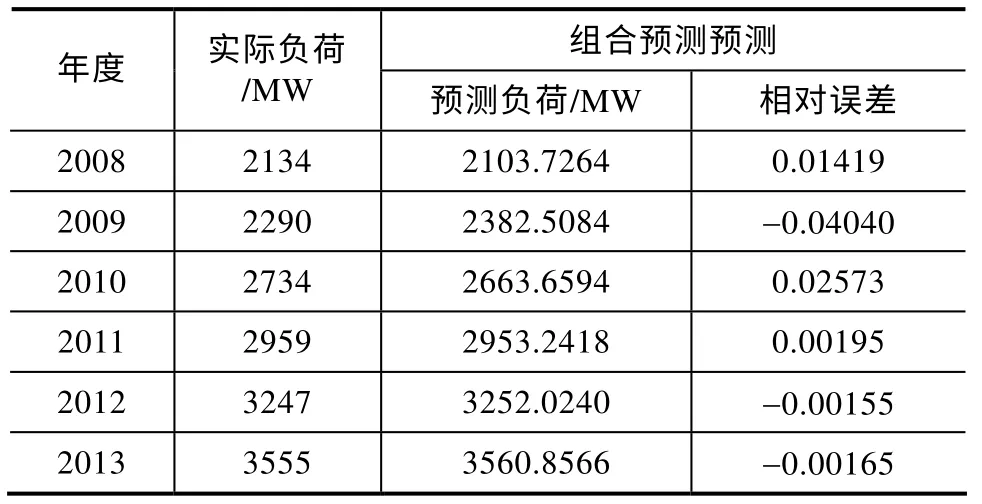
表4
6 结论
本文以线性回归模型、二次多项式模型以及灰色预测模型为基础构造出方差-协方差组合预测模型。通过实例结果,说明与单一的预测模型相比,该方差-协方差组合模型预测出的电力负荷结果精度更高,更具可行性。
因此未来6年的电力负荷预测结果见表5。
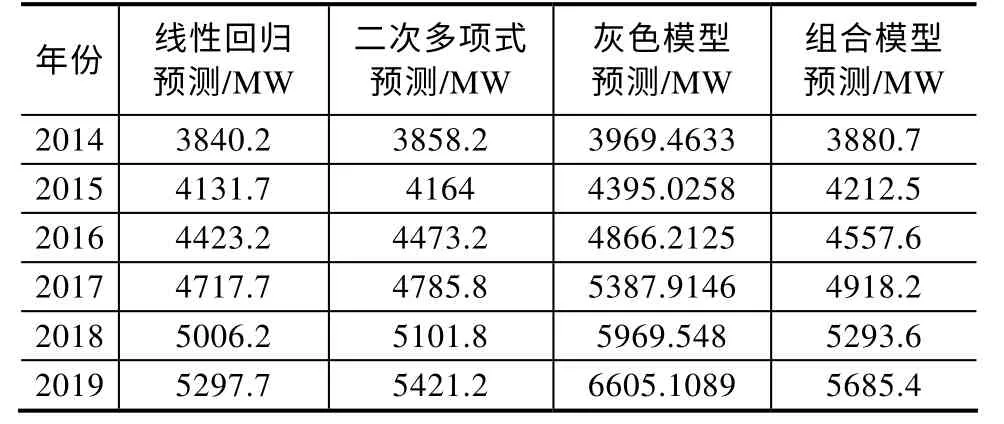
表5
[1] 称浩忠,张焰,等. 电力系统规划[M]. 北京: 中国电力出版社,2008.
[2] 黄业文. 测量误差二次多项式回归模型的参数估计[J]. 武汉船舶职业技术学院学报,2009(4): 59-61.
[3] 徐聪颖,廖峰,陈震海. 灰色组合模型在中长期电力负荷预测中的应用[J]. 电力需求侧管理,2011,13(2): 20-21.
[4] 甘霖. 组合预测模型在中长期电力负荷预测中的应用[D]. 南昌: 南昌航空大学,2012.
[5] 李泓泽,郭森,王宝. 基于最小二乘组合灰色模型的中长期电力负荷预测[J]. 水电能源科学,2012,30(8): 188.
[6] 冯晋. 电力系统中长期负荷的预测[D]. 成都: 四川大学,2004.
