基于数据的废纸配比预测纸浆白度的研究
2015-05-23沈文浩叶文轩
沈文浩 刘 章 叶文轩 焦 东
(1.华南理工大学制浆造纸工程国家重点实验室,广东 广州,510640;2.广州造纸股份有限公司,广东 广州,510281)
对于废纸来源和纤维种类的划分,美国等发达国家已经建立了非常完善的废纸回收标准和制度,回收的废纸分类准确,杂质含量少。废纸种类不同,其纤维种类、成分以及性能等差异很大,直接决定了不同种类的废纸浆性能之间的差异。通常,纸厂会采购多种不同种类的废纸,以混合制浆的方法来保证纸浆品质[1]。影响废纸浆性能的因素有很多,如纤维原料、制浆方法、打浆工艺、印刷加工方法、纤维循环回用次数、存放时间和环境条件等[2-5]。
掌握废纸配比与废纸浆性能之间的关系对于以废纸为原料的造纸企业来说具有重要的意义。例如,提前预知粗浆塔出口处纸浆白度对于后续漂白阶段减少化学品用量、降低生产成本具有积极的作用。由于影响废纸浆性质的因素多且具有很大的不确定性,因此废纸浆的性能指标与废纸配比之间往往存在高度非线性关系,难以建立机理模型。目前,对于利用废纸制浆的造纸企业,废纸配比的选择主要是凭借人工经验,导致废纸浆的性能指标与预期存在很大差异。
与其他质量稳定的造纸原料相比,废纸来源和品质受多方面因素的影响,不同种类的废纸之间存在明显的差异,如8#美废、10#美废、37#欧废等,无论是碎浆后浆料的白度,还是浮选与漂白后浆料的白度初始值明显不同,各工段后浆料白度的增值也不尽相同[6-7]。考虑到纸厂生产过程中的历史数据已经隐含了废纸原料的诸多特性,因此利用数据挖掘与机器学习的方法,可以直接建立废纸配比与废纸浆性能指标之间的关系模型[8],为纸厂确定合适的废纸配比提供科学的定量方法。本课题利用某纸厂3年的废纸浆检测数据和对应的废纸配比数据,选择支持向量机 (SVM)和BP神经网络的方法,在MATLAB软件平台下建立废纸配比与废纸浆白度指标之间的预测模型。
1 建模方法
1.1 BP神经网络
人工神经网络的原理是利用神经元节点之间的数学关系建立出能模拟复杂函数关系的网络[9]。目前越来越多地作为一种可供选择的数学工具来处理各领域中的问题,如系统辨识、预测、模式识别、分类、过程控制[10]。人工神经网络中最受关注的是BP神经网络[11],大多数神经网络结构都采用BP神经网络的结构。典型的BP神经网络是一个全神经网络,即包含3层结构:输入层、隐藏层和输出层,每一个神经元的输出可由式 (1)来描述。
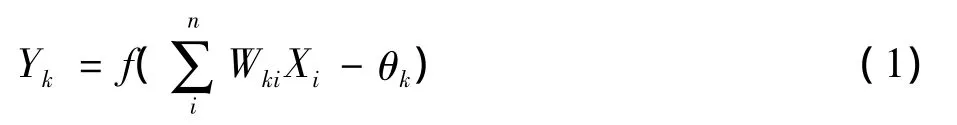
式中,Xi为输入信号,Wki为神经元权值,θk为神经元阈值,f(x)为神经元传递函数,Yk为神经元输出。
BP算法是基于误差最小化原则,即模型以实现期望值与预测值之间误差最小为目的。神经网络在训练过程中就是要寻找合适的权值,这个过程实质上可视为一个非线性无约束最小化问题[12]。
1.2 支持向量机 (SVM)
SVM是建立在统计学理论基础之上的新一代机器学习算法。从最初的应用于模式识别扩展到回归拟合,这种新方法正在获得越来越多的关注。SVM基于结构风险最小化原则,寻找出由训练误差和置信范围组成的泛化误差的最小上限[13]。
对于非线性回归,基本思想是通过一个非线性映射Φ:Rn→H将样本点映射到高维特征空间H,并在高维特征空间中进行线性回归,从而得到在原空间的非线性回归估计。回归估计函数见式 (2)。
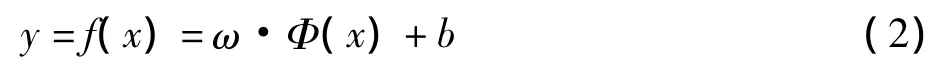
经过推导、引入内积核函数后,SVM的回归函数式 (2)写成式 (3)[14]。
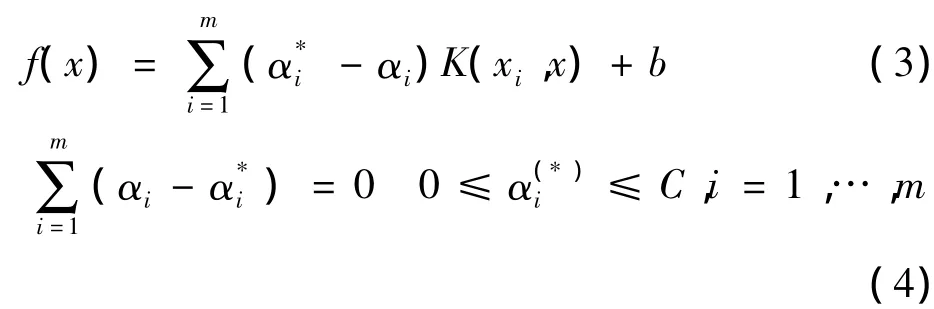
αi、是推导过程中引入的拉格朗日乘子,它们满足式 (4)条件。K(xi,x)是引入的核函数。
2 研究对象
数据来源于某纸厂废纸制浆生产线3年 (2011—2013年)的废纸配比和废纸浆检测数据,该生产线是以100%废纸为原料制浆,生产新闻纸,图1是其制浆工艺流程简图。
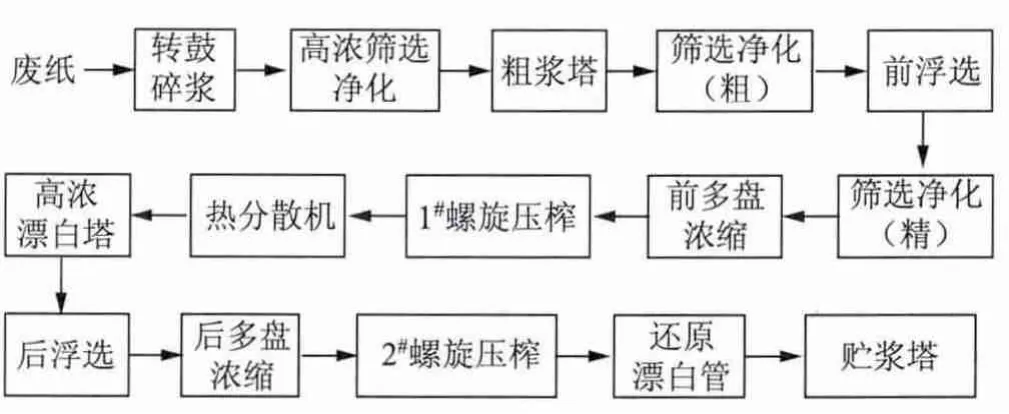
图1 某纸厂废纸制浆工艺流程简图
纸厂3年中使用的废纸种类共10种,其中以8#美废为主,用量平均占比超过60%。另外还用到其他种类的废纸,如10#美废、日本废纸、国内废纸等。3年间,由于废纸供应量、供应价格和纸浆性能要求等因素的影响,该厂更换了138次废纸配比。
纸厂关注的废纸浆性能指标分别是粗浆塔出口处纸浆的白度和灰分,以及贮浆塔送浆泵出口处纸浆的打浆度和抗张强度。根据相应的TAPPI标准离线测量得到以上纸浆性能指标,检测方法和检测频率如表1所示。

表1 纸浆性能指标的检测方法和检测频率
3 结果与讨论
3.1 数据预处理
为了保证数据的可靠性,对数据进行预处理是建模前必不可少的步骤。
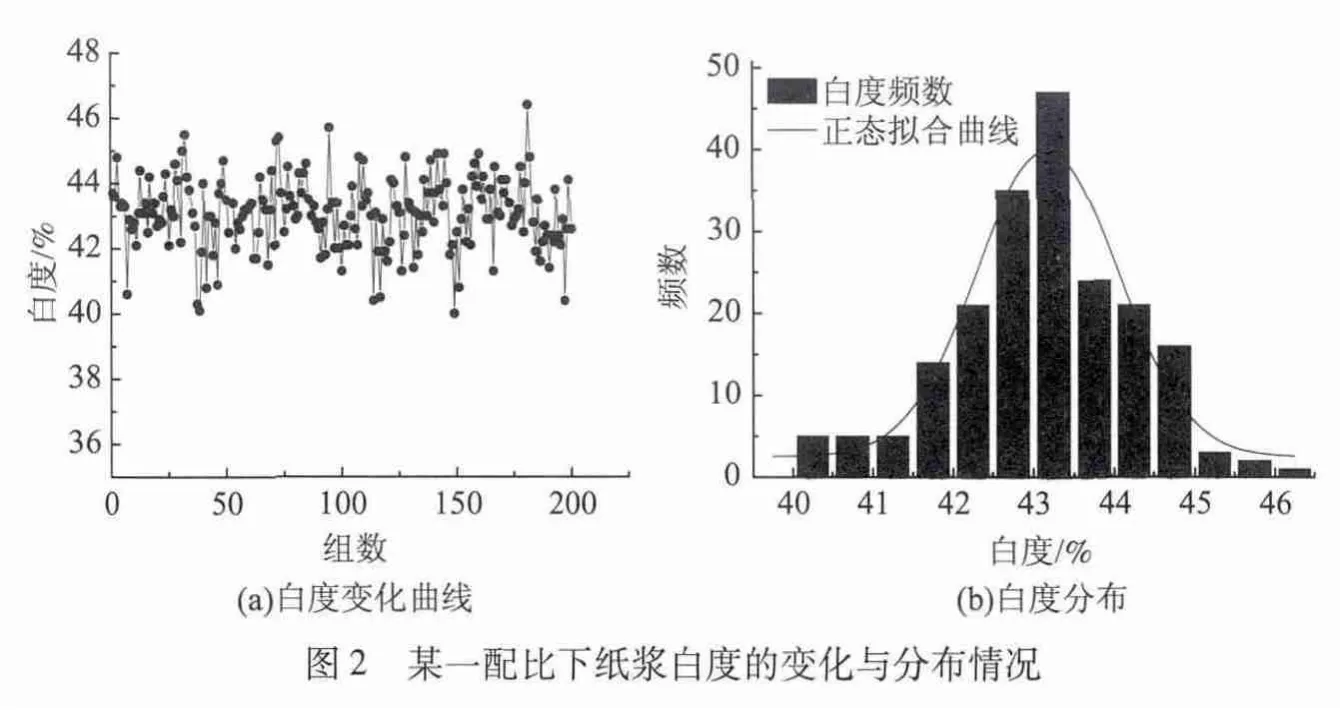
随机选择一组配比,该配比下的白度数据有200个。图2(a)是这段时间内粗浆塔出口处纸浆白度的变化曲线。从图2(a)可以看出,在同一废纸配比下,白度是波动的,变化范围为40%~46.4%。波动的原因推测如下:随着季节和供应商的改变,同一种废纸本身存在质量差异,即使采用同一配比,纸浆的性能指标也会有明显不同。图2(b)是这组白度数据的频数直方图,经过正态分布拟合后,可以看出白度数据大致服从正态分布,即服从N(μ,σ2),其中μ值是该组数据的平均值,σ是该组数据的标准差。采用3σ准则 (拉依达准则)对数据中的不可靠点进行剔除,超过该区间的数据被认为不可靠,予以剔除[15]。
为提高管理成效,学校有必要健全管理制度,制定一系列规章制度,增加思想教育管理的内容,要提高德育部门对思想教育管理工作的关注度。学校要树立人本理念,要将学生、家长引入到学校的管理中,不搞一言堂,涉及到思想教育问题交由学生会决策处理,要经过讨论形成科学有效的规章制度。管理是为了教育学生、维持教育教学秩序,促进学生综合素质的发展。学校管理制度的制订也要扬长避短,要尽量采纳学生提出的合理建议,舍弃不合理的因素。管理制度也要兼顾教育者、被教育者的客观实际,兼顾人性化、严肃性。
在选定的纸浆性能指标中,由于白度测量频繁,数据信息量较大,采用 [μ-2σ,μ+2σ]作为数据的可信区间;对于数据量相对较少的打浆度、抗张强度和灰分,采用 [μ-3σ,μ+3σ]作为可信区间。预处理后纸浆各性能指标的数据量如表2所示。
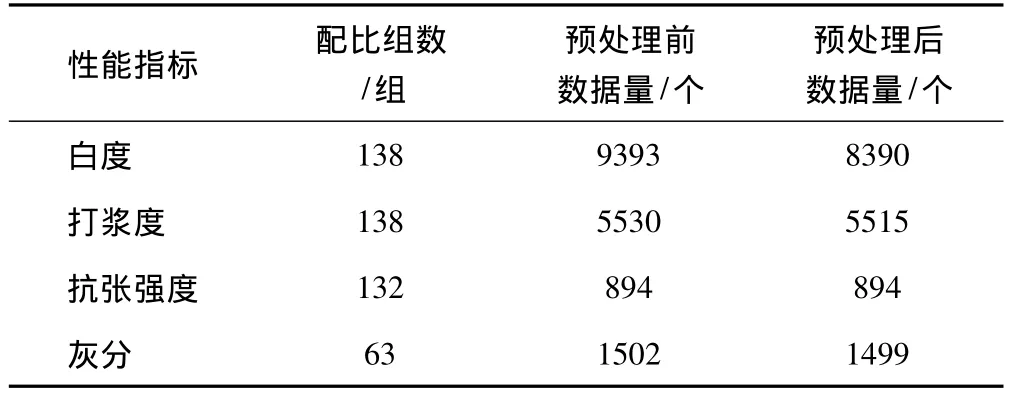
表2 预处理前后纸浆各性能指标数据总量对比
从表1和表2可以看出,由于纸浆白度指标测量频繁,数据量最多,而且也是纸厂目前最关注的纸浆性能指标,所以,下文只介绍通过废纸配比建立纸浆白度的预测模型,其他纸浆指标的预测方法类同。
3.2 建立模型的影响参数
3.2.1 BP神经网络预测模型
本研究中10种废纸的用量都会影响纸浆的白度,所以,根据BP神经网络的建模原理,确定输入层神经元个数为10(X1,X2,…X10),输出层的神经元个数为1(Y1)。由于只含有一个隐含层的3层BP神经网络就能以任意精度逼近一个连续函数[16],因此选取标准的3层BP神经网络进行建模。
图3所示为该3层神经网络的结构图。目前并没有准确公式可以推导出隐含层的个数,通常的办法是选择几种不同神经元个数,进行模型预测能力的比较,确定出合适的神经元个数[17]。本研究分别以隐含层神经元个数 (20,50,100)组建3组不同的BP神经网络,通过比较发现神经元个数为50的BP神经网络精度最高,因此确定隐含层神经元个数为50。根据实际训练时间和模型的收敛情况,利用MATLAB训练BP神经网络的参数为:允许最多训练步数1000步,学习速率0.1,训练最小误差0.0001。
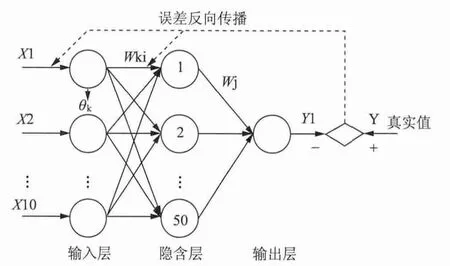
图3 建立纸浆白度预测模型的3层BP神经网络结构图
3.2.2 SVM预测模型
SVM的许多特性是由所选择的核函数来决定的,不同的核函数所表现的特性各不相同,因而由它们所构成SVM的性能也完全不同。目前,SVM的核函数可分为两大类:全局核函数和局部核函数。鉴于组合的混合核函数兼有全局核函数和局部核函数的优点[18],本研究中SVM核函数采用多项式核函数和径向基核函数组合的混合核函数,这样SVM具有更好的泛化能力,也具有很好的学习能力。
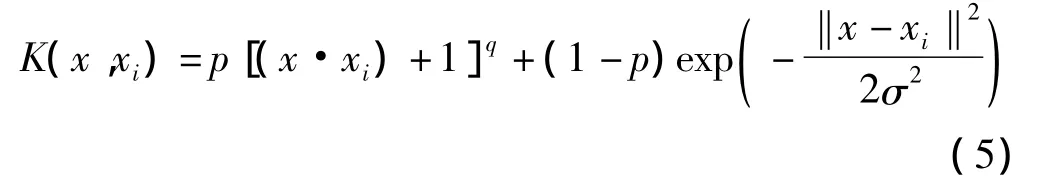
除了核函数的选择以外,SVM的参数选择对模型的影响也较大,需要选择较佳的参数组合。与前面BP神经网络参数选取方式类似。
p选取 (0.5,0.7,0.85,0.95),q选取 (1,2,3),σ2选取 (2-10,2-9,…,29,210),惩罚因子C 选取 (2-10,2-9,…,29,210),经过组合训练,比较模型精度后,确定合适的训练参数为:p=0.85,q=1,σ2=1,C=4。
将表2中的138组配比数据随机分为两部分,其中130组作为训练集,8组作为测试集,对预处理后的白度数据分别使用上述的BP神经网络和SVM方法,用训练集建立废纸配比预测纸浆白度的数学模型,用测试集测试训练好的预测模型,平均相对误差(MRE,Mean Relative Error)用于评价预测精度。
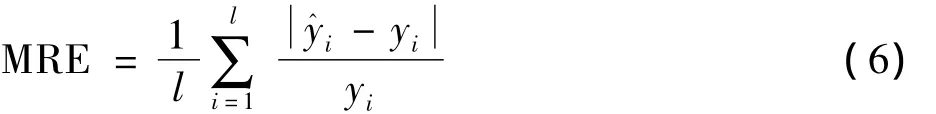
下面是预测模型的建立和测试结果,建模数据分别是全部样本数据和样本均值数据。
3.3 全部样本数据建模
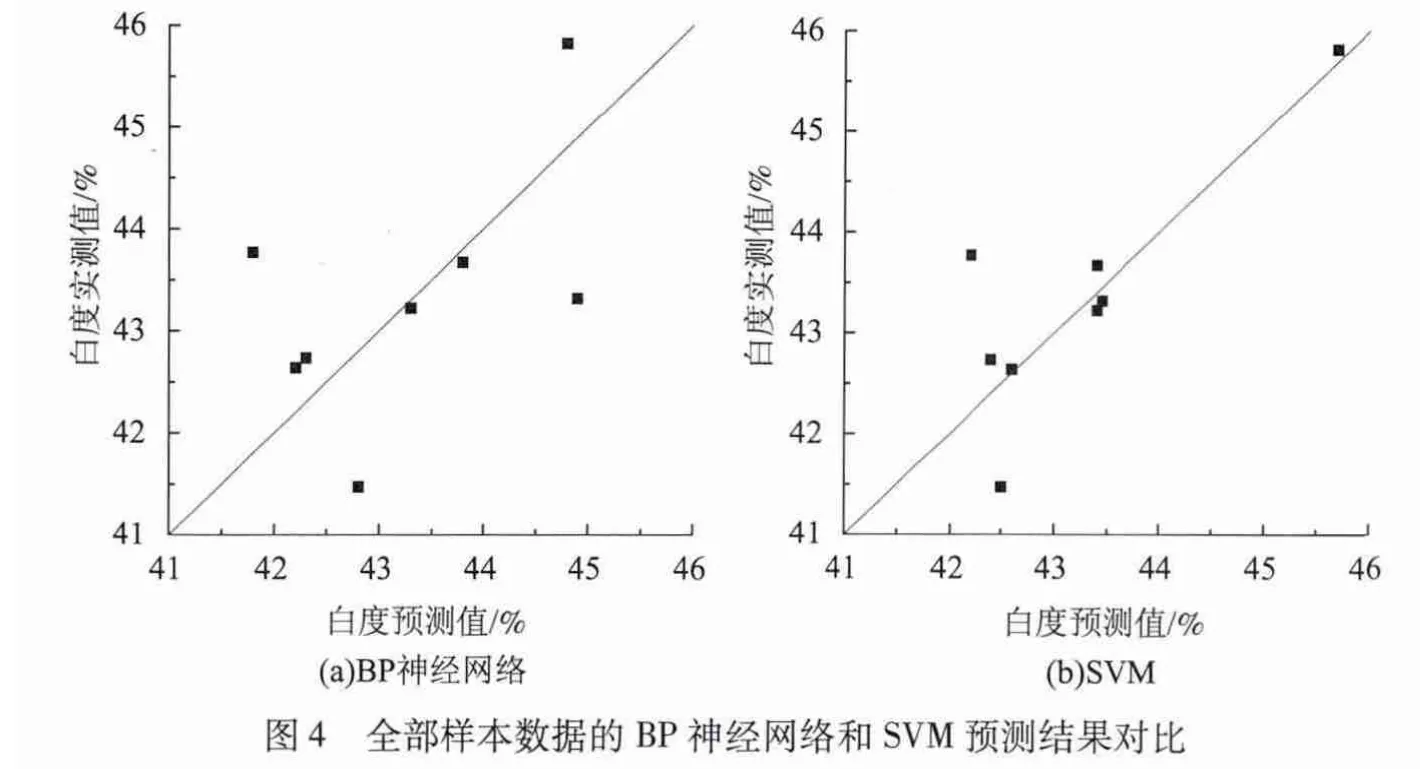
利用全部样本数据建立预测模型,即指利用每一组配比下所有的白度数据,分别采用BP神经网络和SVM方法,建立依据废纸配比预测纸浆白度的数学模型。以每组配比下所有白度数据的平均值作为该配比下的白度实测值,图4是8组测试集中纸浆白度的预测值和实测值对比结果。从图4可以看出,BP神经网络和SVM都能够合理预测出纸浆白度,但图4(b)中的数据点较图4(a)更靠近直线X=Y,同时表3中的1次试验数据也说明SVM的预测精度较BP神经网络的高。
为了避免随机误差,保持训练集和测试集的数据量不变,但每次随机组合训练集和测试集重复进行10次建模和测试,分别记录BP神经网络和SVM的预测结果。图5是利用两种建模方法,对测试集进行10次预测的平均精度对比。由图5可以明显地发现,无论训练集和测试集如何组合,SVM的预测精度普遍优于BP神经网络。
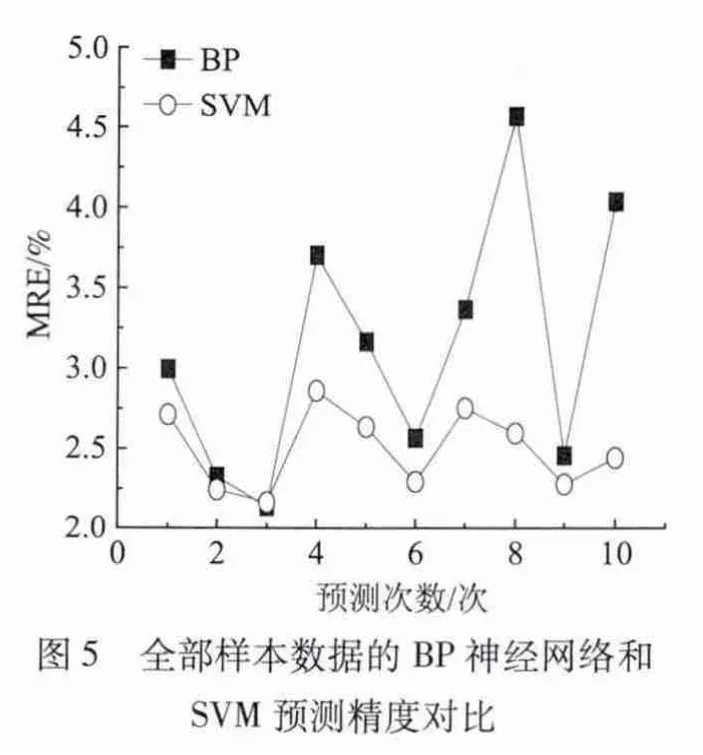
同样的预测结果也体现在表3中,表3列出了分别采用两种建模方法进行1次试验和10次试验的模型预测精度和训练时间。可以看出,不论是1次试验还是10次试验,SVM的预测精度均比BP神经网络的高。但是,SVM预测模型的训练时间远远大于BP神经网络的训练时间。这主要是由于SVM是借助二次规划来求解支持向量,而求解二次规划将涉及n阶矩阵的计算 (n为样本个数),当n数目很大时该矩阵的存储和计算将耗费大量的机器内存和运算时间,因此,使用某一配比下全部白度数据建立预测模型,SVM的运算量远远大于BP神经网络,相应需要更多的训练时间。
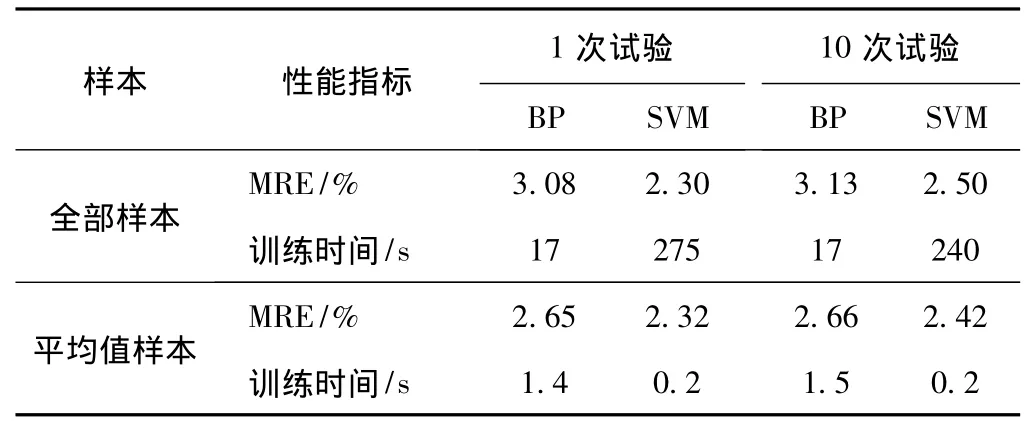
表3 不同样本数据集的BP神经网络和SVM性能对比
3.4 样本平均值数据建模
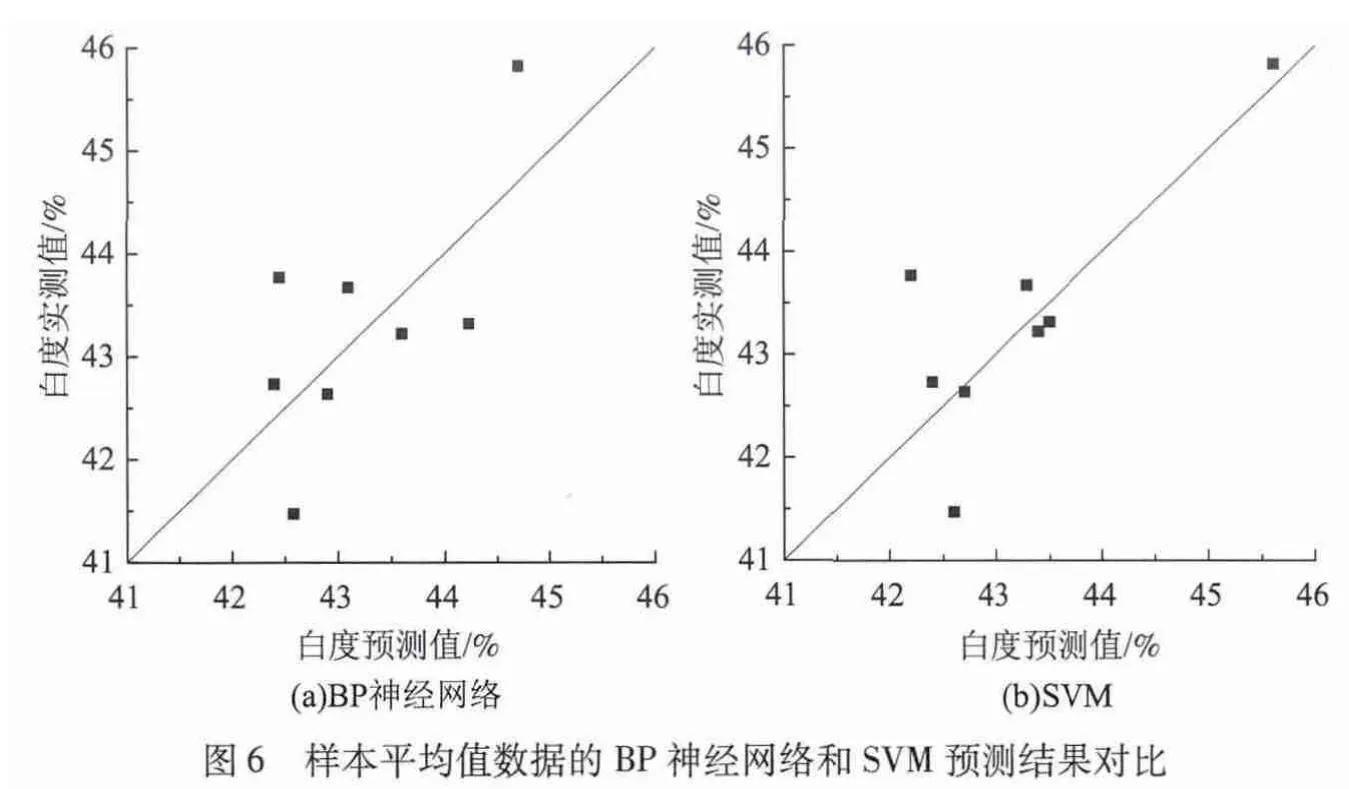
由图2(b)可知,纸浆白度数据近似服从正态分布,因此,针对上述使用全部样本数据建模需要较长训练时间的缺陷,可以采用一组配比下的所有白度数据的平均值作为该配比下的纸浆白度参考值。基于以上思路,同样随机选择表2中130组数据作为训练集,8组数据作为测试集,此时一组配比对应唯一的纸浆白度真实值。分别利用BP神经网络和SVM方法建立纸浆白度预测模型。预测结果如图6所示,同样可以发现,图6(b)中的数据点较图6(a)更靠近直线X=Y,同时表3中的1次试验数据也说明SVM预测模型的精度略优于BP神经网络模型。
同样地,重复进行10次建模和测试,图7是利用两种建模方法,对测试集进行10次预测的平均精度对比。由图7可以看出,总体上,SVM的预测相对误差小于BP神经网络的相对误差。同时,表3的数据进一步说明采用样本平均值数据作为数据集,SVM的预测精度仍然优于BP神经网络。需要特别指出的是使用样本平均值数据建立预测模型所需的训练时间明显缩短,特别是对于SVM建模方法。
预测结果表明,使用样本平均值数据建模时,虽然SVM模型的预测精度变化不大 (如图8(b)所示),但是BP神经网络的预测效果显然有较明显的提升 (如图8(a)所示),预测精度提高了15%。这主要有两方面原因,一是利用平均值数据使得一组配比下的白度指标唯一确定,而不是在一定范围内波动;另一方面,全部数据中,每一组配比下白度指标的检测次数并不相同,检测次数多的必然会对模型有较大的影响。
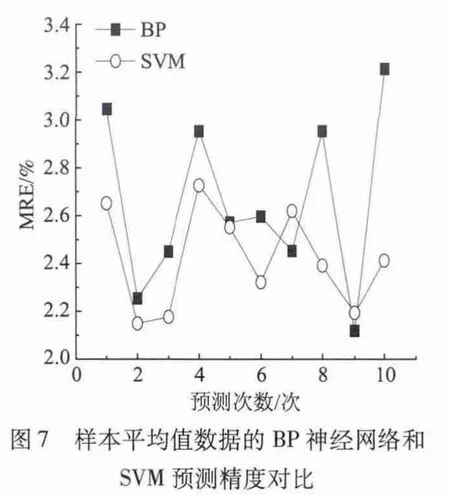
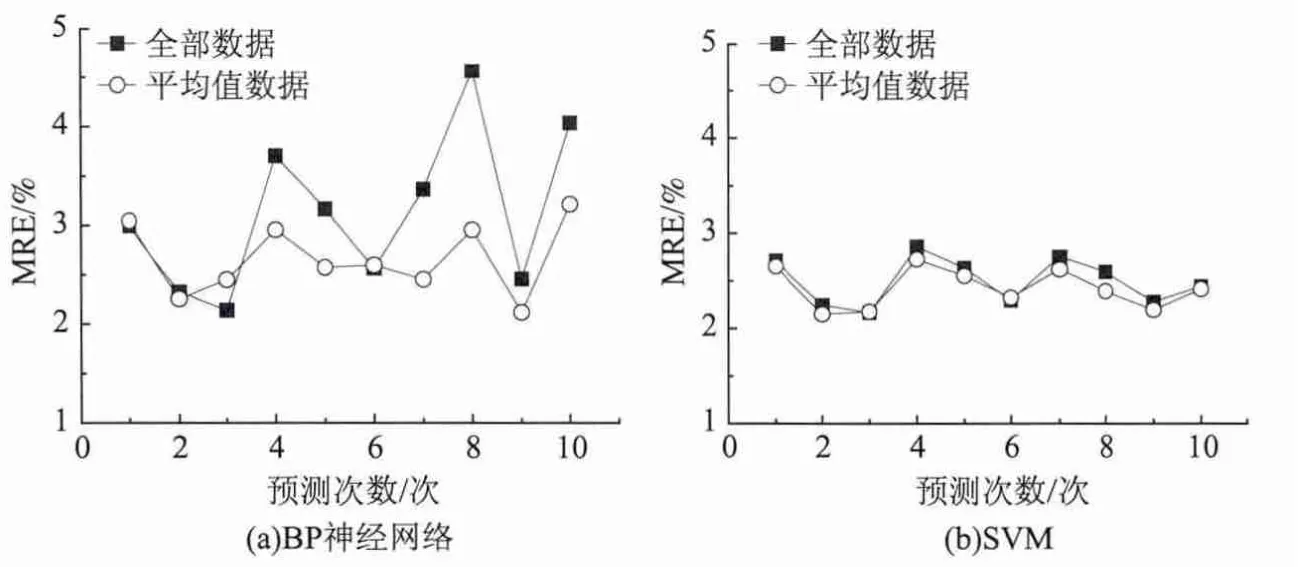
图8 全部样本数据和平均值样本数据建模的预测精度比较
表4所示为BP神经网络模型和SVM模型的预测性能对比。由表4可知,SVM预测模型的相对误差波动范围ΔMRE均低于BP神经网络,说明SVM方法的预测稳定性较好;与利用全部数据作为数据集相比,用样本平均值数据作为建模数据集,BP神经网络模型的预测精度提升了15%,模型训练时间缩短为全部数据建模的8.8%;SVM模型的预测精度虽然仅提高了3%,但是模型训练时间缩短为全部数据建模的0.08%。综合表4中的数据可以看出,以样本平均值数据作为数据集,采用SVM方法建立的预测模型,不仅有较好的预测精度 (2.42%)和良好的稳定性 (0.58%),而且模型训练时间短 (0.2 s),完全可以应用于实际生产过程,这样既有利于模型参数的优化,又方便新样本数据加入时实现模型的及时更新。
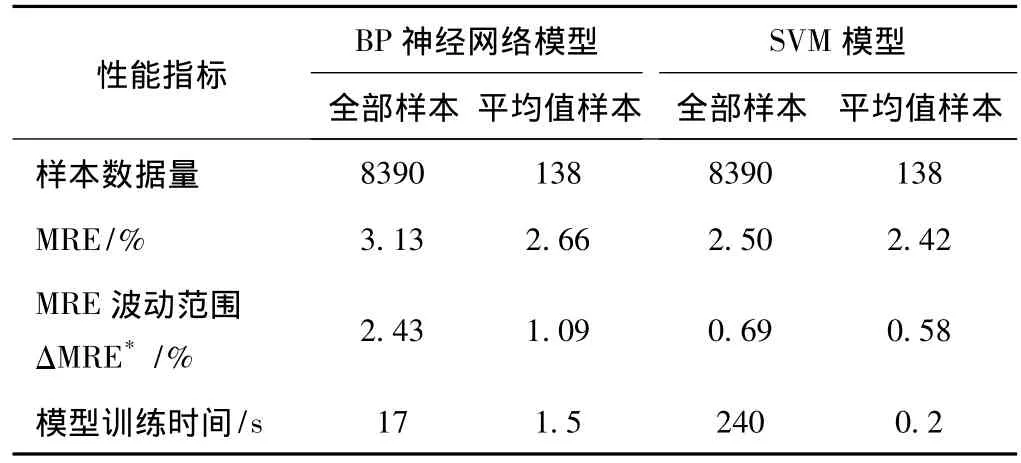
表4 BP神经网络模型和SVM模型的预测性能对比
4 结论
本课题基于某纸厂废纸制浆生产线3年的废纸配比和废纸浆性能检测数据,分别采用BP神经网络和支持向量机 (SVM)的建模方法,建立了基于废纸配比预测纸浆白度的数学模型。研究发现,与BP神经网络相比,SVM预测模型的预测精度普遍较高,误差波动范围更小,稳定性更高;BP神经网络模型和SVM模型的训练时间均大幅缩减,其中尤以SVM模型为甚,其模型训练时间缩短为使用全部样本数据建模所需的0.08%。这说明数据集的选择对模型的预测精度同样起着至关重要的作用,全部数据固然包含大量的信息,但是建模算法很难完全提取出有效的信息,相反可能会降低预测模型的精度和增加运算时间。综合考虑模型预测精度、预测稳定性以及模型训练时间等因素可以确定:以样本平均值数据作为建模数据集,采用SVM方法建立纸浆白度预测模型,既能保证有较好的预测精度 (2.42%)和良好的稳定性(0.58%),而且模型训练时间短 (0.2 s),所建立的预测模型精度可以满足实际生产过程的需要,其极短的训练时间也方便使用新样本数据进行预测模型更新,以保证其实时性。
基于所需的纸浆白度反向推选出最优废纸配比,并进一步考虑废纸的价格、市场供应等多重因素,推选出最优废纸配比,是本课题后续的研究,这将为造纸企业的废纸采购和配比选择提供决策支持。
[1]Zhu Xiao-mei.Application of Different Kinds of Waste Paper in Deinking Pulp Production[J].Paper Science & Technology,2013(6):22.朱晓梅.不同种类废纸在脱墨浆生产中的应用实践[J].造纸科学与技术,2013(6):22.
[2]Zhan Huai-yu.The classification of waste paper and the changes in regeneration process——one of the waste paper recycling technology lectures[J].Paper Science & Technology,1999(1):50.詹怀宇.废纸的分类及其再生过程性质的变化——废纸回用技术讲座之一[J].造纸科学与技术,1999(1):50.
[3]Okwonna O.The effect of pulping concentration treatment on the properties of microcrystalline cellulose powder obtained from waste paper[J].Carbohydrate Polymers,2013,98(1):721.
[4]Zhan Huai-yu,Chen Jia-xiang.Pulping Principle and Engineering[M].Beijing:China Light Industry Press,2011.詹怀宇,陈嘉翔.制浆原理与工程[M].北京:中国轻工业出版社,2011.
[5]CHEN Jia-xiang.Research Process in Pulping Technology of Waste Paper[J].China Pulp & Paper,2003,22(2):43.陈嘉翔.废纸制浆技术的研究进展[J].中国造纸,2003,22(2):43.
[6]LIU Cheng-liang,LIU Shu-guang,ZHAO Nian-zhen,et al.Pulping Properties of Waste Paper From Different Sources[J].China Pulp &Paper,2012,31(5):9.刘成良,刘曙光,赵年珍,等.不同废纸脱墨制浆性能的研究[J].中国造纸,2012,31(5):9.
[7]HU Hui-ren,LI Hai-ming,ZHANG Pen.Preliminary Study on Deinked pulp Bleaching[J].China Pulp & Paper,2005,24(3):5.胡惠仁,李海明,张 盆.脱墨浆高白度漂白初步研究[J].中国造纸,2005,24(3):5.
[8]Tao Jin-song,Yang Ya-fan,Li Yuan-hua.Comparsion of paper tensile strength prediction models based on PLS and SVM methods[J].Journal of South China University of Technology:Natural Science Edition,2014(7):132.陶劲松,杨亚帆,李远华.基于PLS和SVM的纸张抗张强度建模比较[J].华南理工大学学报:自然科学版,2014(7):132.
[9]Sha W,Edwards K L.The use of artificial neural networks in materials science based research[J].Materials & Design,2007,28(6):1747.
[10]Mjalli F S,Al-Asheh S,Alfadala H E.Use of artificial neural network black-box modeling for the prediction of wastewater treatment plants performance[J].Journal of Environmental Management,2007,83(3):329.
[11]Sadeghi B H M.A BP-neural network predictor model for plastic injection molding process[J].Journal of Materials Processing Technology,2000,103(3):411.
[12]Ju Q,Yu Z B,Hao Z C,et al.Division-based rainfall-runoff simulations with BP neural networks and Xinanjiang model[J].Neurocomputing,2009,72(13-15):2873.
[13]Su Xing,Li Huai-de,Long Hui-long.The study on temperature prediction model for dry gas-to-ethylbenzene reactor's outlet based on support vector machine[J].Computers and Applied Chemistry,2011(11):1372.苏 兴,李怀德,龙回龙.基于支持向量机的干气制乙苯反应器出口温度预测模型研究[J].计算机与应用化学,2011(11):1372.
[14]Cao L J,Tay F E H.Support vector machine with adaptive parameters in financial time series forecasting[J].IEEE Transactions on Neural Networks,2003,14(6):1506.
[15]Cheng D W,Han D,Wang W Y,et al.Study on the Fast Judgment of Abnormal Value with Excel.Proceedings of 20122nd International Conference on Computer Science and Network Technology[C]//New York:IEEE.2012.
[16]Jing G L,Du W T,Guo Y Y.Studies on prediction of separation percent in electrodialysis process via BP neural networks and improved BP algorithms[J].Desalination,2012,291:78.
[17]Labidi J,Tejado A,Garcia A,et al.Simulation of tagasaste pulping using soda-anthraquinone[J].Bioresour Technol.,2008,99(15):7270.
[18]Lu Rong-xiu.Application of mixed kernel function SVM in the system modeling[J].Journal of East China Jiaotong University,2010(2):63.陆荣秀.混合核函数支持向量机在系统建模中的应用[J].华东交通大学学报,2010(2):63.
