基于异质策略型顾客的损失厌恶型 零售商决策研究

□刘 珩

[惠州学院 惠州 516007]

引言

时尚消费品的市场竞争越来越激烈，在销售季中制造商家一方面需要加大投入使商品升级换代速度加快来吸引满足消费者需求，例如苹果公司的iphone 4S手机在时隔半年就推出了iphone 5；另一方面，零售商家又要面对2008年金融危机以来由于世界经济前景的不确定性而导致消费者在购买商品时越来越谨慎。产品销售季中，如何刺激消费者购买是当前国内外零售商面临亟待解决的问题。国内部分家电零售商、汽车销售商常采用频繁降价或捆绑销售来刺激消费者购买，例如差价返还等策略[1]。国外有的电器零售商、服装制造零售商，例如Best Buy、Gap、Zara等，还采用客户关系管理方法来区分消费者，例如短视消费者、策略消费者和廉价品消费者[2～4]，在此基础上通过减少库存来加大缺货风险，加快消费者购买。

产品销售季中，基于策略型消费者（消费者差异性和零售商-消费者之间的价格博弈），学者们从定价和库存策略两个维度进行了研究。从定价角度，Su研究了市场中同时存在策略消费者与非策略消费者时零售商的动态定价问题[5]。Aviv和Pazgal指出零售商面对策略型顾客可制定两种价格来获取最大利益[6]。Peng和Xiong提出零售商可对顾客承诺退货价格来应对策略型顾客的估价不确定[7]。李娟等研究了基于策略型消费者在两级市场下的购买行为，认为回购合同可以实现供应链最优[8]。从库存策略角度，Cachon和Swinney指出快速补货可以减少期初订购量并缓解消费者策略行为[3]，认为快速时尚响应模式在面对同质策略消费者时可更好地匹配供需[4]。Liu和van Ryzin认为销售可分为两个阶段来分别适应策略型消费者和短视型消费者的购买，给出了两个阶段的最优库存数量[2]。从定价-库存策略角度，Shen和Su认为零售商引入动态价格和库存机制可减少策略型顾客的等待行为[9]。在上述研究的基础上，学者考虑基于策略型消费者存在时的产品质量决策。Sang-Hyun Kim和Swinney认为短视消费者和策略消费者存在时，零售商可通过制定高保留价格-低保留价格来标识商品的库存状况和质量[10]。黎维斯和任建标认为消费者市场中除了短视消费者和策略型消费者外，还存在因清仓价格而产生的廉价品消费者，在此基础上考虑了零售商面对三种类型消费者时订货决策与生产商的产品质量决策[11]。这些文献都是研究基于风险中性零售商-异质型消费者存在时的最优决策。

一般的报童模型基于零售商风险中性、消费者只是零售价格接受者和单次消费的假设来构建模型和提供最优决策。生活实践发现，个体决策者还有风险追逐型、风险中性型和风险厌恶型。学者们运用各种风险工具对报童模型中的决策者类型进行了扩展，例如前景理论、均值方差模型、VaR等，证明了：若不考虑零售商缺货损失，风险厌恶型零售商的最优订货量小于风险中性零售商的最优订货量；若存在零售商缺货，由于有消费者评价直接影响零售商信誉，因此风险厌恶零售商型的最优订货量可以大于风险中性零售商的最优订货量[12～16]。现有文献中尚未有考虑风险偏好零售商-异质型消费者存在时的研究。

本文用前景理论刻画零售商损失厌恶度，考虑风险厌恶零售商面对短视消费者、策略型顾客和廉价品消费者时的订货策略，构建零售商决策模型，揭示零售商的最优订货量与零售商（风险厌恶度、清仓价格和销售损失）；策略型消费者（非短视消费者比例）；批发价格的关系；市场风险的关系。

一、问题描述

销售周期开始前，生产商以批发价格w供货给零售商。市场中的消费者有三种类型，短视消费者、策略型消费者和廉价品消费者，他们先后在正常销售期和清仓期进行购买[11]。

短视消费者对商品的保留价格为mv。短视消费者只在正常销售期出现。廉价品消费者只会在商品清仓期才出现，他们完全不会考虑购买全价商品。策略消费者对商品的保留价格为v，v为独立同分布的随机变量。消费者知道自己的保留价格但零售商和生产商不了解，但分布函数G（v）为消费者、零售商和生产商的共同知识。假定G（v）是[0,U]上的均匀分布，其中U为消费者保留价格的最大值。策略消费者在正常销售期和清仓期都会出现。λR（≥1）表示零售商的损失厌恶度，1Rλ=时表示风险中性零售商，Rλ越大表示零售商越厌恶损失。

假设实际需求量是商家期望需求D与期望为1的正随机变量的乘积，市场实际需求量的概率密度函数为g（x）=f（x/D）/D。销售周期开始后，消费者根据商品零售价格p决定是否购买。gR表示销售过程中由于商品缺货导致的零售商销售损失。清仓期商品价格为s，销售季结束后，零售商将剩余库存商品退给生产商，本次商品销售结束。对商品的价格，直观的有p＞w＞s。

二、零售商的最优订购策略

根据文献[11]结论，市场中的消费者，短视消费者、策略型消费者和廉价品消费者，他们占消费者比例分别为1-α、1-（p-φs）/（（1-φ）U）和（p-s）/（U-s），其中，φ为策略消费者在清仓期中得商品购得率，α∈[0,1]。令A=1-（p-φs）α/（（1-φ）U）和B=（1-A）/φ，其中A∈（0,1），B∈（0,1）。

零售商订货量为Q时，其利润 ∏R（Q）按市场需求量分别为pQ-gR（x-Q）-wQ，x＞Q/A；pAx+s（Q-Ax）-wQ，Q/A≥x≥Q/（A+B）；pAx+sBx-wQ，Q/（A+B）＞x＞0。第1种情况下，（p+gR-w）Q/gR＞x时，有∏R（Q）＞0；第2种情况下，x＞（w-s）Q/（A（p-s））时，有∏R（Q）＞0；第3种情况下，x＞wQ/（pA+sB）时，有∏R（Q）＞0。

运用前景理论，得到零售商的期望效用为

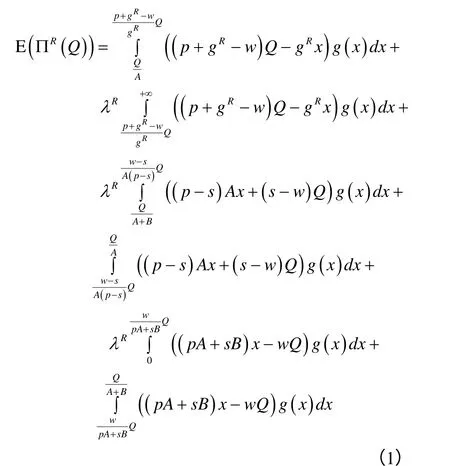
令y=x/D，化简式（1）得到

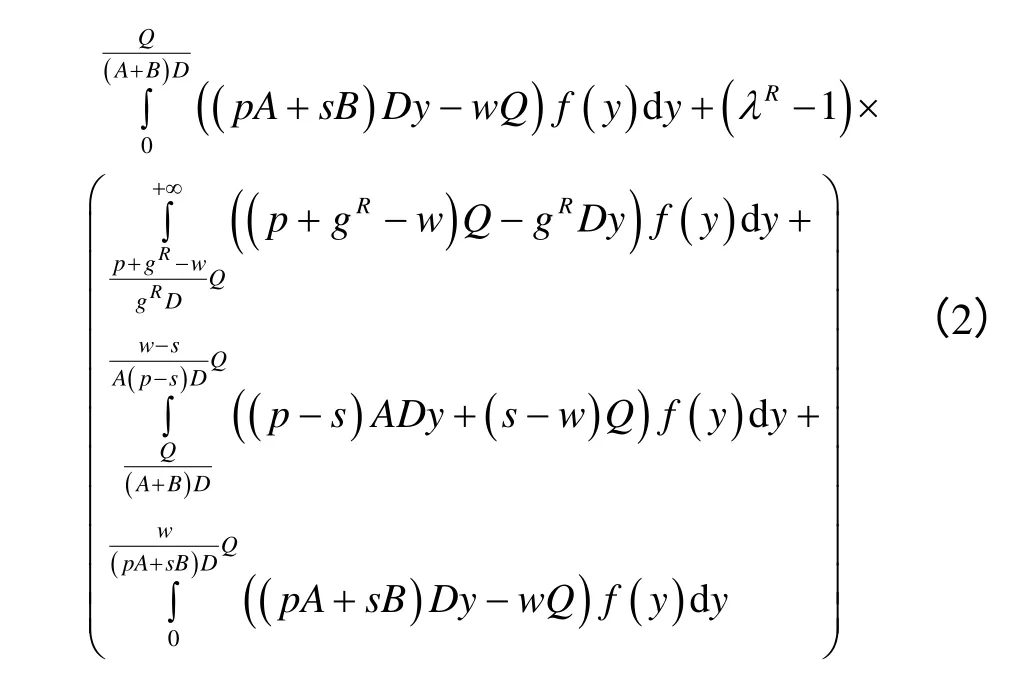
令∂E（∏R（Q））/∂Q=0，得到最优订货量Q*满足下式：

假设函数f（y）=1/（2e），e∈[0,1]，y表示为[1-e,1+e]之间的均匀分布；e表示市场需求标准差[11]，e越大表示市场风险越大。

解式（3）得到

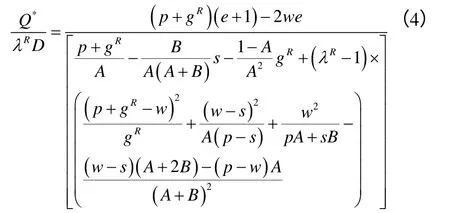
令Ψ1=p/gR，Ψ2=w/gR，ψ3=s/gR

化简式（4）得到

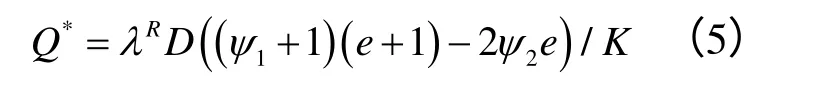
三、零售商的最优订货量分析

证明：首先，证明没有清仓价格时最优订货量存在。接着证明有清仓价格时最优订货量Qs*＞0大于没有清仓价格时的最优订货量。

（1）容易知道Ψ1＞Ψ2，Ψ2/Ψ1=w/p。

当λR=1，s=0时，容易证明＞0，因此Q*＞0，即最优订货量存在。

因为

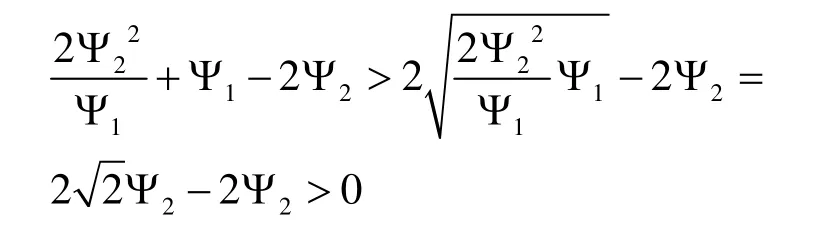
且

所以对方程

（2）当 λR＞1，s＞0时，式（4）中，对s求导，得到＜0，即

定理1证毕。

定理2 最优订货量与零售商损失厌恶度的关系有：（1）没有清仓价格时，最优订货量随λR的增大而减少；（2）有清仓价格时，若清仓价格使得

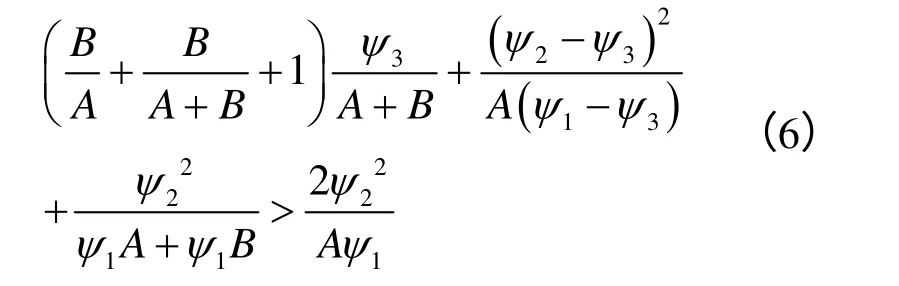
证明：Q*对λR求导，得到：

首先，证明没有清仓价格时最优订货量和λR的关系。接着证明有清仓价格时最优订货量和λR的关系。

（1）当s=0时，简化得到

由A=1-φB得到B=（1-A）/φ，B/（A（A+B））=（1-A）/（A（φA+ 1-A））。

因为

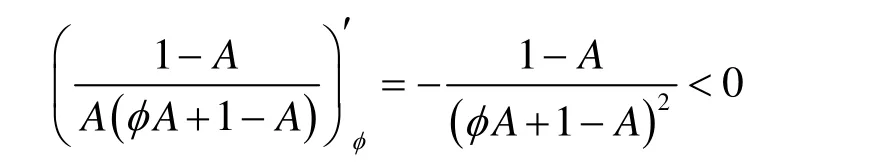
所以有

从而有

又由定理1中知道

（2）当s＞0时，因为对的分子部分，有

对∂Qs*＞0/∂λR的分子部分，有

若

则ΔF=Fs＞0-Fs=0≤0，即Fs＞0≤Fs=0＜0。

定理2（2）证毕。

定理3 最优订货量与缺货损失的关系有：（1）：没有清仓价格时，最优订货量Qs*=0随缺货损失gR的增大而增大；（2）有清仓价格时，若清仓价格使得

证明：Q*对gR求导，得到和gR的

（1）s=0时，

将A=1-pα/（（1-φ）U）和φ=（U-p）/U代入∂Qs*=0/∂gR，简化得到

由于（（1-2α）/α）′α=-1/（α2）＜ 0，因此有

由于（e/（e+1））′e=1/（e+1）2＞0，因此有

从而得到p+2（1-2α）ew/（α（e+ 1））＞0。

由定理1知道

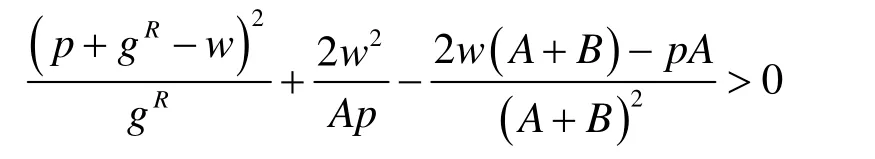
零售商销售单位商品得到的利润p-w，缺货造成的损失为gR，如果p-w＜gR，那么零售商为避免损失发生，必然为满足所有消费者而采购，而这在现实生活中一般是不可能的，因此假设p-w＜gR不成立，则有p-w≥gR，（p+gR-w）（p-gR-w）≥ 0。

综合上述3项，得到 ∂Qs*=0/∂gR的分子部分大于零，因此∂Qs*=0/∂gR＞0。定理3(1)证毕。

（1）s＞0时，分子为

与s=0时的分子相减，得到

由（1）知道Fs＞0＞0，因此若Fs＞0-Fs=0＞0时，则Fs＞0≥Fs=0＞0，即

定理3（2）证毕。

定理4 最优订货量与策略型消费者（非短视消费者比例）的关系有：（1）风险中性零售商的最优订货量随非短视消费者比例的增加而减少；（2）若清仓价格使得K1＜0，损失规避型零售商的最优订货量随非短视消费者比例的增加而减少；若K1＜0，最优订货量随非短视消费者比例的增加而增加。其中，

K对α求导，并简化得到

若1=，则有

定理4（1）证毕。

又因为 ∂A/∂α=-（p-φs）/（（1-φ）U）＜ 0，

因此，当K1＜0时，∂K/∂α＞0，∂Q*/∂α＜ 0；当K1＞0时，∂K/∂α＜0，∂Q*/∂α＞0。

定理4（2）证毕。

定理5 最优订货量与批发价格的关系有：（1）风险中性零售商的最优订货量Q*随批发价格w增加而减少；（2）有清仓价格时，若清仓价格使得K2＞0，则损失规避型零售商的最优订货量Q*随批发价格w增加而增加；若K2＜0，则最优订货量Q*随批发价格w增加而减少。

证明：Q*对w求导，简化后得到因此，若λR=1，得到∂Q*/∂w＜0。当K2＞0时，∂Q*/∂w＞0；当K2＜0时，∂Q*/∂w＜0。证毕。

定理6 当gR＞2w-p时，最优订货量Q*随市场风险e的增大而增大；当gR＜2w-p时，最优订货量Q*随市场风险e的增大而减小③。

证明：Q*对e求导， 简化后得到：

∂Q*/∂e=λRD（Ψ1+1-2Ψ2）/K。

当Ψ1+1-2Ψ2＞0时，∂Q*/∂e＞0；当Ψ1+1-2Ψ2＜0时，∂Q*/∂e＜0。即当gR＞2w-p时，∂Q*/∂e＞0；当gR＜2w-p时，∂Q*/∂e＜0。证毕。

四、结 论

市场中消费者一方面期望商家提供的商品越来越时尚，另一方面受金融危机影响在购买商品时越来越谨慎，消费者购买行为的变化促使零售商把顾客多样性和市场风险纳入到订货决策中。本文运用前景理论刻画零售商损失厌恶度，考虑零售商面对短视消费者、策略型顾客和廉价品消费者时的订货策略。研究表明，没有清仓价格时损失厌恶型零售商的最优订货量小于有清仓价格时的最优订货量；没有清仓价格时，最优订货量随零售商损失厌恶度增大而减少，但随缺货损失的增大而增大；当零售商运用清仓价格来吸引潜在消费者时，只有在一定条件下，损失厌恶型零售商的最优订货量随损失厌恶度、缺货损失、非短视消费者比例、批发价格和市场风险的增加而减少。这就要求零售商要选择制定好清仓价格以获取最大效用。未来研究中，可以在此研究基础上考虑零售商存在运营资金约束下的最优决策。

注释

①定理1解释了为什么现在零售业广泛进行“清仓（价）”宣传广告来吸引潜在消费者购买商品。

②经典报童模型中，一般不考虑缺货损失。随着商家对商誉的日益重视，缺货损失对订货决策的影响得到关注。研究表明，有缺货损失时的订货决策与没有缺货损失时的决策是有区别的。

③gR＞2w-p时，由定理3中知道p-w≥gR，因此得到p＞1.5w，即零售商在进价的基础上加价50%以上进行销售。这个在现实生活中存在这样的实例，比如2009年菜市场中出现的“蒜你恨”哄抢现象，2009年3月底时，其出库价即批发价每吨200～300元，从4月11日开始，每吨猛然涨了将近100元；2009年6月，每吨700余元；8月，每吨1200元；11月，每吨4000元；12月，每吨7000元。

[1]SU Xuanming,ZHANG Fuqiang.On the value of commitment and availability guarantees when selling to strategic consumers[J].Management Science,2009,55(5):713-726.

[2]LIU Qian,VAN RYZIN G.Strategic capacity rationing to induce early purchases[J].Management Science,2008,54(6):1115-1131.

[3]CACHON G P,SWINNEY R.Purchasing,pricing,and quick response in the presence of strategic consumers[J].Management Science,2009,55(3):497-511.

[4]CACHON G P,SWINNEY R.the Value of fast fashion:Quick response,enhanced design,and strategic consumer behavior[J].Management Science,2011,Articles in Advance:1-18.

[5]SU Xuan ming.Intertemporal pricing with strategic customer behavior [J].Management Science,2007,53(5):726-741.

[6]AVIV Y,PAZGAL A.Optimal pricing of seasonal products in the presence of forward-looking consumers [J].Manufacturing & Service Operations Management,2008,1(4):1-21.

[7]PENG Z Q,XIONG Y.Value uncertain in advance selling:the impact of offering refunds for cancellations [A].International Conference on Service Operations and Logistics,and Informatics[C].Beijing:IEEE,2008:64-68.

[8]李娟,黄培清,顾锋.基于顾客战略行为下的供应链系统的绩效研究[J].中国管理科学,2007,15(4):77-82.

[9]SHEN Z J M,SU X M.Customer behavior modeling in revenue management and auctions:a review and new research opportunities[J].Production and Operations Management,2007,16(6):713-728.

[10]SANG H K,SWINNEY R.Product quality choice and inventory risk with strategic consumers[Z].Yale working paper,2011.

[11]黎维斯,任建标.基于异质策略消费者的订货与质量决策[J].西南民族大学学报,2012,38(1):113-118.

[12]SCHWEITZER M E,CACHON G P.Decision bias in the news vendor problem with a known demand distribution:experimental evidence[J].Management Science,2000,46(3):404-420.

[13]WANG C X,WEBSTER S.The loss-averse news vendor problem[J].Omega,2009,37(1):93-105.

[14]CHOI T M,LI D,YAN H,CHIU C H.Channel coordination in supply chain with agents having mean-variance objectives [J].Omega,2008,36(4):565-576.

[15]WU J,LI J,WANG S,CHENG T C E.Mean-variance analysis of the news vendor model with stock out cost[J].Omega,2009,37(3):724-730.

[16]黄松,杨超,张曦.考虑客户战略行为时报童模型定价与库存控制[J].运筹与管理,2010,19(3):15-22.