混合Bernoulli分布参数估计的EM算法研究

张宝龙，魏立力

（宁夏大学 数学计算机学院，宁夏 银川 750021）

成败型随机试验在统计学上称为伯努利试验（Bernoulli trial）.很多实际问题都可以归结为伯努利试验.比如在医学领域考察对病人治疗结果的有效与无效、某种化验结果的阳性与阴性、接触某传染源的感染与未感染等；在系统可靠性理论中元件工作正常与失效；决定人类的某一特别属性（比如是否为左撇子）的一对基因的显性表现与隐性表现；某陪审团的陪审员对被告人的投票结果为有罪和无罪等等.伯努利试验必须满足两个基本条件：每次试验的结果独立且只有“成功”与“失败”，每次试验中“成功”的概率保持不变.

伯努利试验的一种推广是假设每次试验相互独立，但其成功概率允许不尽相同.这样的情形可以用一个混合Bernoulli分布来描述：

其中所有πj≥0,且…,pl)为未知参数.如果希望考察某种药物对患者的疗效（有效或无效），则该模型非常适用，因为我们很难保证同种药物对不同患者的疗效完全相同.也就是说，我们预期对于众多患者的疗效可以分成l个不同的类别.

现在设y=(y1,y2,…,yn)来自于混合Bernoulli分布(1.1)的样本，我们的目的是求未知参数θ=(π1,π2,…,πl-1,p1,p2,…,pl)的极大似然估计.为此先考查其对数似然函数：

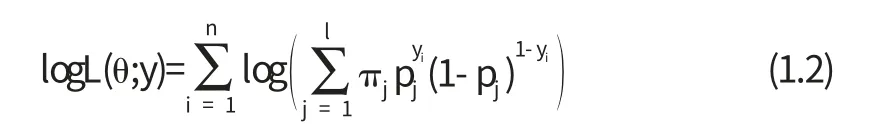
不难看出，直接求(1.2)式的最大值点是很困难的，我们下面将推导该问题的EM算法.

EM算法是一种迭代计算，其每次迭代由两步组成：E步（求条件期望）和M步（极大化），这正是该算法名称的由来.该算法最初由Dempster，Laird和Rubin提出[1]，主要用来求后验分布的众数（极大似然估计），广泛应用于删失数据，截尾数据，成群数据等.其基本思想是在给出缺失数据初值的条件下，估计出模型参数的值；然后再根据参数值估计出缺失数据的值.根据估计出的缺失数据的值再对参数值进行更新，如此反复迭代，直至收敛，迭代结束.

EM算法提出之后，很快引起国内外众多学者的关注，文献[2]很好地总结了EM算法及其推广算法的很多成果.文献[3]详细介绍了有限混合模型及其应用.文献[4]介绍了有限混合模型及其应用的研究进展.本文基于EM算法研究了有限混合Bernoulli分布模型的参数估计，并利用R软件进行了数值模拟.

1 EM 算法简介

一般而言，形式上[1]我们有两个样本空间X,Y，以及X到Y的一个多对一映射xay(x).其中X中x=(x1,x2,…,xn)不能直接观测到，只能通过y间接的观测到，x被称为“完全数据”.Y里的y=(y1,y2,…,yn)是能够观测到的数据，即“不完全数据”.

设参数θ∈Θ,x的密度函数为fc(x|θ),则y的密度函数为

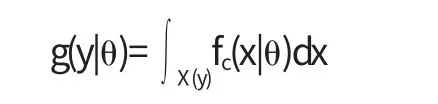
其中X(y)={x:y(x)=y}

我们的目的是求参数θ 的极大似然估计，对坌θ∈Θ,使得g(y|θ)极大化.令x=(y,z)表示y的完全数据，其中z=(z1,z2,…,zn)表示不可观测数据或缺失数据，即将yi,i=1,…,n用缺值扩张为xi=(yi,zi).由于在具体问题中，极大化不完全数据的密度函数g(y|θ)往往要比极大化完全数据的密度函数fc(x|θ)困难很多.EM算法就是试图通过极大化后者（或者对数似然函数）而达到极大化g(y|θ)的目的.但是由于x不能被观测到，从而logfc(x|θ)未知，我们的策略是用logfc(x|θ)在给定y和θ(k)（经过k次迭代后的值）下的条件期望来代替.

具体地说，设θ(0)是θ 的初值.则在第一次迭代中，E步需要计算

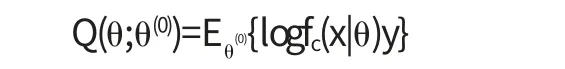
M步则需要关于θ 最大化Q(θ;θ(0)).也就是求θ(1)使得

重复执行E步和M步，但是这次用θ(1)的当前值来代替θ(0)，然后极大化得到θ(2)作为下一次迭代的初值.则在k+1次迭代时，E步和M步可以被定义如下:

简单和稳定是EM算法的最大优点，EM算法所得到的估计序列具有良好的收敛性，且收敛到g(y|θ)的最大值.具体而言，记估计序列为θ(k),k=1,2,…,L(θ|y)=logg(y|θ),则在关于L的很一般的条件下，θ(k)的收敛值θ*是L的稳定点[1].

2 有限混合Bernoulli 分布模型参数估计的EM 算法

设离散型随机变量X服从有限混合Bernoulli分布，其概率函数为(1.1)式，设)是来自于该分布的简单随机样本，其似然函数为(1.2)式，我们的目的是求未知参数θ=(π1,π2,…,πl-1，p1,p2,…,pl)的极大似然估计.下面我们讨论相应的EM算法.

引入潜在变量z=(z1,z2,…,zn)，其中z=(zi1,zi2,…,zil)，且z1,z2,…,zn相互独立，zij是取值为0或1的指示变量，zij=1表示yi来自于第j个分支密度，且

于是有yi|zij=1:B(1,pj),j=1,2,…,l.这样可以得到完全样本为xi=(zi,yi),i=1,2,…,n,其似然函数为

对上述似然函数取对数并去掉与π1,π2,K,πl-1,p1,p2,K,pl无关的量，得

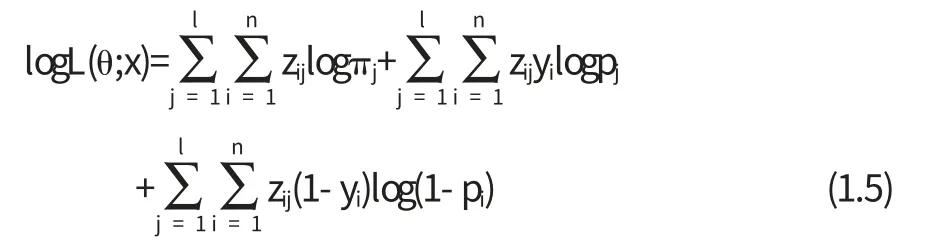
在E步中，令

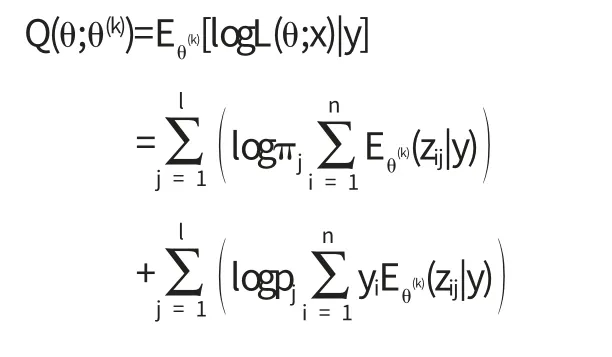
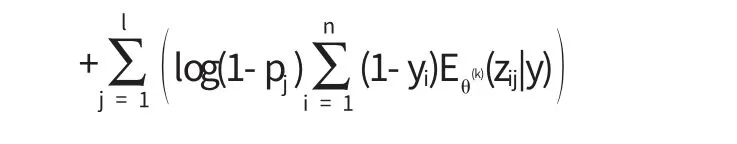
易知

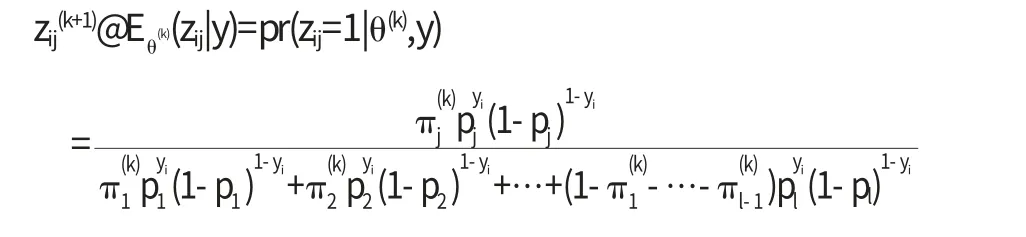
在M步中，解

得到

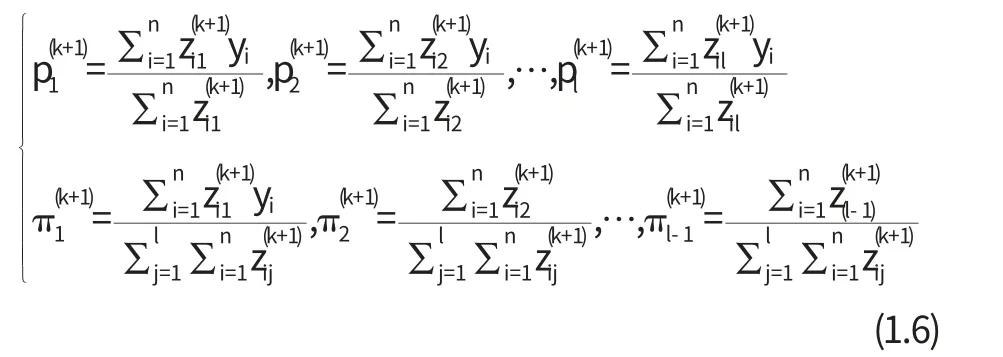
基于以上导出的迭代公式，用R软件进行参数估计的算法如下：

1.产生n个来自有限混合Bernoulli分布的随机变量；

3.令k=1，将2中的初值代入迭代公式(1.6)中，得到θ(k)；

4.k→k+1，将θ(k)代入迭代公式(1.6)中，得到θ(k+1)；

5.重复4，直至||θ(k+1)-θ(k)||充分小时停止.

以二阶混合二项分布为例：模拟1中随机变量Y的算法为

1.产生服从参数为(1,p1)的二项随机变量Y1；

2.产生服从参数为(1,p2)的二项随机变量Y2；

3.产生随机数U；

4.若U<π，令Y=Y1；否则令Y=Y2；

3 数值模拟

下面用R统计软件进行随机模拟.

第一种情况：建立混合模型0.4B(1,0.3)+0.6B(1,0.5)，分别产生500个和1000个来自该混合模型的随机数，选取三组不同的初值为

表1 混合模型0.4B(1,0.3)+0.6B(1,0.5)参数估计结果

表2 混合模型0.4B(1,0.3)+0.6B(1,0.5)参数估计结果

第二种情况：建立混合模型0.4B(1,0.3)+0.6B(1,0.5)，分布产生100个、500个、1000个来自该混合模型的随机数，选取初值为π(0)=0.4,p1(0)=0.1,p2(0)=0.2.进行数值模拟，EM算法参数估计结果见表3.

从表1和表2可以明显看出,随着初值逐渐接近真值时，估计值亦趋于真值.当估计值变化不大时，说明估计值收敛到稳定点.由表3可以看出，随着样本容量的增加，参数的估计值逐渐接近于真值.同样，当估计值变化不大时，说明估计值收敛到稳定点.

〔1〕Dempster A P，Laird N.Maximum Likelihood from Incomplete Data via EM Algorithm[J].J.Royal Statistical Society，Series B，1977，39:1-38.

〔2〕Gelffrey J.McLachlan.The EM Algorithm and Extensions(Second Edition)[M].New York: Wiley & Sons，Inc，2008.

〔3〕McLachlan G，Peel D.Finite Mixture Models[M].New York:Wiley&Sons，Inc，2000.

〔4〕孙兰.有限混合模型及其应用的研究进展[D].长春:东北师范大学，2006.

〔5〕魏立力，马江洪，颜荣芳.概率统计引论[M].北京:科学出版社，2012.