力的动态平衡分析法

陈天瑜

动态平衡即某一过程中物体处于一系列的平衡状态下，物体所受合力虽恒为零，但组成合力的“成员”作用在发生变化. 分析这类问题，可采用控制变量的思想，先定量研究某参量确定下的一个平衡态，得到各“成员”的变化规律，再讨论该参量变化时各“成员”的变化情况.

平行四边形定则是力、运动、加速度等所有矢量的合成与分解都遵循的矢量运算的最基本定则.

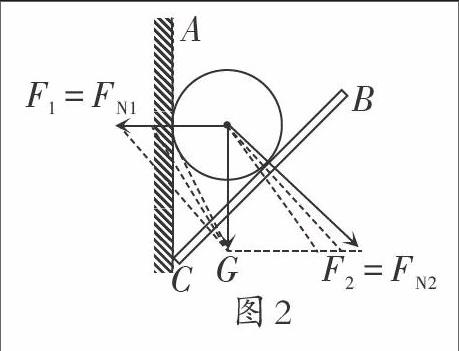
例1 如图1所示，把球夹在竖直墙AC和木板BC之间，不计摩擦. 设球对墙的压力为FN1，球对板的压力为FN2，则在将板BC逐渐放至水平的过程中（ ）

A. FN1和FN2都增大

B. FN1和FN2都减小

C. FN1增大，FN2减小

D. FN1减小，FN2增大

解析 虽然题目中的FN1和FN2涉及的是墙和木板的受力情况，但研究对象还是只能取球. 在将板[BC]逐渐放至水平的过程中，球时刻处于动态平衡状态，FN1和FN2都是变力，可以先画开始时刻的受力图，然后再根据力的关系讨论力的变化规律.

方法一：分解法. 球所受的重力[G]产生的效果有两个，一是球对墙的压力FN1，二是球对板的压力FN2. 根据这两个效果将其分解，则F1=FN1，F2=FN2，如图2所示，从动态变化图中不难看出，在板[BC]逐渐放平的过程中，FN1的方向保持不变而大小逐渐减小，FN2与[G]的夹角逐渐变小，其大小也逐渐减小.

方法二：合成法. 由于球处于平衡状态，弹力FN1、FN2的合力F跟重力是一对平衡力，其大小、方向均不变，如图3甲所示，画出力的矢量三角形如图3乙所示，在板[BC]逐渐放平的过程中，除合力F恒定外，墙对球的弹力FN1的方向也不改变，而FN2绕[O]点为轴顺时针转动，α角逐渐减小到0，可以看出，FN1、FN2都逐渐减小，当木板水平时，有FN1=0，FN2=[G].

由此推出，在[BC]板逐渐放平的过程中，α角减小，FNl、FN2都逐渐减小. 选B项.

点拨 动态平衡问题的处理，往往有多种方法，比如列公式或画图. 公式法的局限性比较大. 图象法可分为合成法和分解法. 如果是三个力使物体平衡，可合成其中的两个变力，它们的合力与第三个力等大反向，通过构成的平行四边形或三角形边长的变化，得出力的变化.

[ 矢量三角形法]

合成与分解的平行四边形问题，实际上也是解三角形问题，利用正弦、余弦定理或相似三角形的知识求解. 对三力平衡的动态分析，也可从受力分析入手，抓住变量与不变量的关系，根据平衡条件和平行四边形定则，把物体所受的三个力集中到三角形中，求解三角形中的边角关系即力之间的关系.

例2 如图4所示，水平放置的粗糙的长木板上放置一个物体[m]，当用力缓慢抬起一端时，讨论木板受到物体的压力和摩擦力将怎样变化.

解析 以物体为研究对象，受力分析如图5甲所示. 可知在抬起木板的过程中，摩擦力的变化是先增加后减小，压力一直减小. 或用三角形法，在物体未滑动时，处于平衡状态，加速度为零，所受三个力围成一个闭合三角形. 由于摩擦力总与支持力垂直，故三力构成直角三角形，可将它们构成一个半圆形，如图5乙所示，从而得出各力变化情况.

例3 如图6所示，用绳将球挂在光滑的墙面上，绳子变短时，讨论绳的拉力和球对墙的压力将如何变化.

解析 从对应的图7甲中的平行四边形或图7乙中的三角形不难看出，当绳子变短时，θ角增大，FN增大，FT变大.

例4 如图8所示，在AC绳上悬挂一重物G，在AC绳的中部O点系一绳BO，以水平力F牵动绳BO，保持AO方向不变. 现使BO绳沿虚线所示方向缓缓向上移动，讨论力F和AO绳上拉力的变化情况.

解析 用平行四边形法（图9甲）或矢量三角形法（图9乙）可以看出，在[BO]绳缓缓向上移动的过程中，[T]变小，[F]先变小后变大.

点拨 三个共点力作用下的动态平衡问题，通常其中一个力大小、方向均不变，如重力，另一个力方向不变，大小变（或大小不变，方向变），如支持力，第三个力大小、方向均改变.

当力构成的三角形与周围有绳或边构成相似三角形之时，往往运用相似三角形法，根据物体所受合力为零，构建封闭的“力矢量三角形”，寻求与力矢量三角形相似的几何三角形，建立比例关系，把力的大小变化问题转化为几何边长的大小变化问题进行讨论.

例5 如图10所示，固定在水平面上的光滑半球，半径为R，球心O的正上方固定一个小定滑轮，细线一端拴一小球，置于半球面上的A点，另一端绕过定滑轮. 现缓慢地将小球从A点拉向B点，讨论在此过程中，小球对半球的压力大小FN、细线的拉力大小FT的变化情况.

解析 小球受力如图11所示，据平衡条件，小球所受的支持力FN和细线的拉力FT的合力F跟重力是一对平衡力，有[F=G]. 据几何关系，力三角形[ΔFAFN]与几何三角形[ΔCOA]相似. 设半球的半径为[R]，滑轮到半球顶点[B]的距离为[h]，线长[AC]为[L]，有[FNR=GR+h=FTL]. 在小球从[A]点移向[B]点的过程中，[G、R、h]均不变，[L]减小，则FN大小不变，FT减小.

点拨 本题由于此变化中支持力FN和细线的拉力FT的方向是往竖直方向靠拢，单纯用图形法无法显示其变化特点.