循环行列式的求法

张慧萍

（内蒙古商贸职业学院社科基础部，呼和浩特 010022）

循环行列式的求法

张慧萍

（内蒙古商贸职业学院社科基础部，呼和浩特 010022）

循环行列式是线性代数中一类特殊的行列式，在实际当中也有其重要的应用。给出循环行列式的概念，通过举例的形式给出简单循环行列式的计算方法，即化为上三角形行列式进行计算，且得到此类行列式的计算公式，进而利用n次多项式的根得到一般循环行列式的计算方法。

循环矩阵；循环行列式；多项式；根

循环行列式是线性代数中一类具有特殊结构的行列式，也是线性代数中的研究热点，在许多的实际问题中都有着广泛的应用。本文首先给出循环矩阵、循环行列式的概念，进而通过举例的方式给出简单的循环行列式的计算方法，最终得到一般的循环行列式的计算方法。

定义1[1]设a1，a2，…，an是n个复数，称矩阵

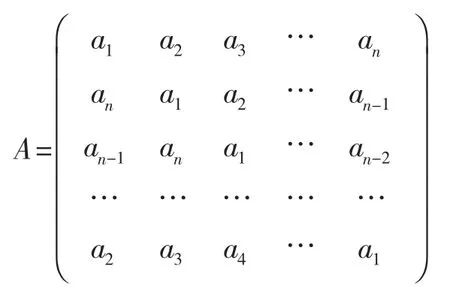
是以a1，a2，…，an为元素的n阶循环矩阵。则循环矩阵A的行列式即为n阶循环行列式。

下面，我们给出一个简单的循环行列式，并给出具体的计算方法，并得到最终的计算公式。

例1计算10阶行列式

分析：这个行列式中的所有元素都是已知的，且没有零元素，若利用行列式的性质将其化为上三角形行列式，则可以得到行列式的结果。

为了能够看清楚行列式的具体构造，我们不妨多写几行几列，在计算中也能够更加方便地得知下一步的计算方法。由于行列式的每行元素都是1，2，…，10这十个数，因此，首先我们可以将第2列到第10列的元素都加到第1列，进而提取公因子进行计算。然后，通过观察，我们发现行列式的第1列元素都是1，所以将第1行的-1倍分别加到第2行到第n行进行消零。再观察所得到的行列式，我们将所得行列式的第2行的i-1倍分别加到第i行上，其中i=3，4，…，9，另外，将第2行直接加到第10行，即得到我们想要的上三角形行列式。最终，行列式的结果即为主对角线元素的乘积。具体的计算过程如下：

解

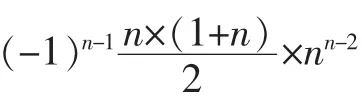
例2计算下面的n阶循环行列式

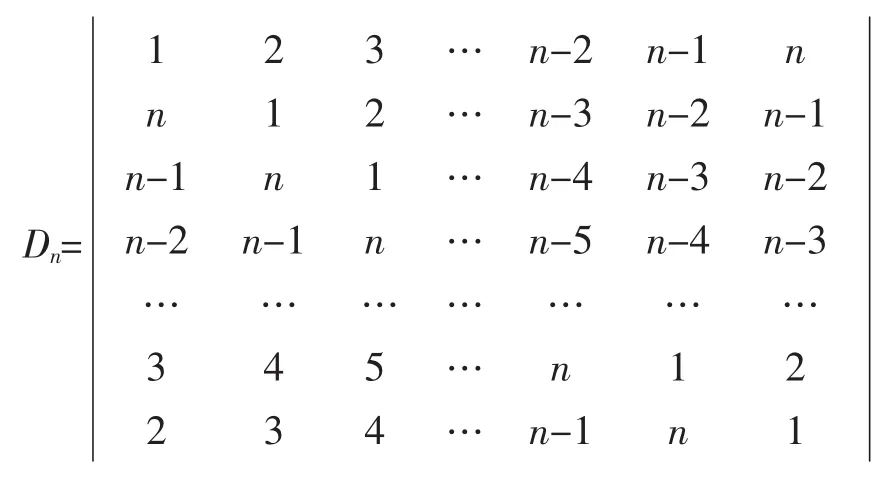
解

由此可知，由例1所猜测的此类n阶循环行列式的结果是正确的，即：

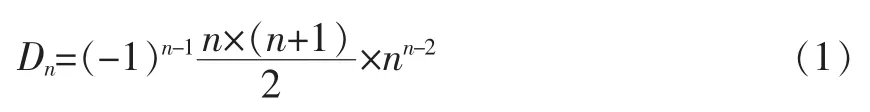
所以，我们遇到此类行列式可以直接套用公式（1）计算即可，为我们计算填空题或选择题提供了方便，也可以为计算类题型计算结果的提供检验。

除了上面例1、例2所给的循环行列式，我们还会遇到变形后的循环行列式，下面我们也给出此类行列式的计算过程及其最终的计算公式。

例3 计算下面的n阶循环行列式

与例2类似的计算方法，我们可以得到此行列式的计算结果为：

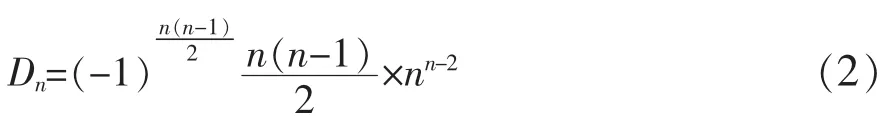
也就是说，此行列式的结果与例2所给行列式的结果在符号上是有区别的，因此，我们把（2）式也作为计算此类循环行列式的一个公式，但在应用的时候要注意的是结果中的符号。

除了上面所给类型的循环行列式，更一般的构造n阶循环行列式的数是a1，a2，…，an这n个复数，对于这样的循环行列式，用上述的计算方法就不是很方便了，因此我们利用多项式的根来进行求解，可以得到下面的结论。

定理1[2]设A是以n个复数a1，a2，…，an为元素的n阶循环矩阵，则矩阵A的行列式，

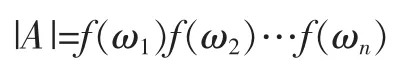
其中，f（x）=a1+a2x+…+an-1xn-2+anxn-1是复数域上的n-1次多项式，ω1，ω2，…，ωn是多项式xn-1的n个根。

利用定理1，我们将其应用于例2，可得Dn= f（ω1）f（ω2）…f（ωn），其中ω1，ω2，…，ωn是多项式xn-1的n个根，且此处，则通过计算可知：

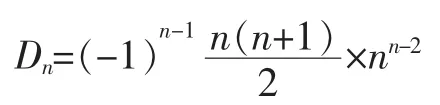
与化为上三角形行列式计算的结果是一致的。

需要说明的是，利用定理1求解n阶循环行列式，要求解n次多项式的n个根，且需将此n个根分别代入n-1次多项式f（x）中进行求值，然后再求乘积，计算量也是比较大的，但要解决由定义1所给n阶矩阵的循环行列式，即构造行列式的n个复数是任意给定时，定理1所给的方法就体现出了优越性。我们在计算的时候可以根据所给行列式的特点自行把握，选择适当的方法进行计算。

[1] 张禾瑞，郝炳新.高等代数[M].北京:高等教育出版社，1979

[2] 贾璐，姚光同，有关循环矩阵行列式的计算及其应用[J].信阳师范学院学报(自然科学版)，2005-4，18（2）

Solution Method of Recurrent Determinant

ZHANG Hui-ping
(Department of Basic and Social Science,Inner Mongolia Business and Trade Vocational College,Huhhot 010022)

Cyclic determinant is a class of special determinant in the linear algebra,and there are important applications in the actual.Gives the conception of the cyclic determinant,by the way of giving examples,obtains the computing method of the simple cyclic determinant, changes into a triangle on the determinant to calculate.And obtains the computational formula of this class determinant,and makes use of the roots of the polynomial of degree n,obtains the computing method to solve the general cyclic determinant.

Circulant Matrix;Recurrent Determinant;Polynomial;Roots

1007-1423（2015）03-0022-04

10.3969/j.issn.1007-1423.2015.03.006

张慧萍（1979-），女，内蒙古乌兰察布人，硕士，研究方向为数学教育教学

2014-12-09

2014-12-30