基于卡方距离度量的改进KNN算法

谢红，赵洪野

哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨 150001

基于卡方距离度量的改进KNN算法

谢红，赵洪野

哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨 150001

K-近邻算法（K-nearestneighbor，KNN）是一种思路简单、易于掌握、分类效果显著的算法。决定K-近邻算法分类效果关键因素之一就是距离的度量，欧氏距离经常作为K-近邻算法中度量函数，欧式距离将样本的不同特征量赋予相同的权重，但是不同特征量对分类结果准确性影响是不同的。采用更能体现特征量之间相对关系的卡方距离度量作为KNN算法的度量函数，并且采用灵敏度法进行特征权重计算，克服欧氏距离的不足。分类实验结果显示，基于卡方距离的改进算法的各项评价指标优于传统的KNN算法。

K-近邻算法；卡方距离；距离度量；二次式距离；欧式距离；灵敏度法

可用于分类的方法有：决策树、遗传算法、神经网络、朴素贝叶斯、支持向量机、基于投票的方法、KNN分类、最大熵［1］等。K-近邻分类算法［2］（K-nearest neighbor，KNN）是Covert和Hart于1968年首次提出并应用于文本分类的非参数的分类算法。KNN算法的思路清晰，容易掌握和实现，省去了创建复杂模型的过程，只需要训练样本集和测试样本集，而当新样本加入到样本集时不需要重新训练。虽然KNN算法有着诸多优点，但也存在着以下不足。首先，分类速度慢、计算复杂度高，需要计算测试样本与所有的训练样本的距离来确定k个近邻；其次，特征权重对分类精度的影响较大。针对上述缺点，一些学者提出相应的改进方法。为了提高分类速度，降低计算复杂度，Juan L［3］建立了一个有效的搜索树TKNN，提高了K-近邻的搜索速度，彭凯等［4］提出基于余弦距离度量学习的伪K近邻文本分类算法，Lim等［5］用向量夹角的余弦引入权重系数，桑应宾［6］提出一种基于特征加权的K Nearest Neighbor算法，来提高分类准确率。文献［7-8］对输入的样本进行简单的线性变换映射到新的向量空间，在新的向量空间对样本进行分类，可以有效提高分类性能。本文主要是对距离度量函数进行改进，用卡方距离度量函数替换欧氏距离度量函数，并在新的度量函数下计算特征量的权重系数，来提高分类的准确率。

1 KNN算法

KNN作为一种基于实例的分类算法，被认为是向量模型下最好的分类算法之一［9］。KNN算法从测试样本点y开始生长，不断的扩大区域，直到包含进k个训练样本点为止，并把测试样本点y的类别归为这最近的k个训练样本点出现频率最大的类别。KNN算法的主要操作过程如下：

1）建立测试样本集和训练样本集。训练样本集表示为

4）选择k个近邻训练样本。对于测试样本点y按照式（1）找到在训练样本集中离测试样本点y最近的k个训练样本点。

5）测试样本y类别的判别规则。即对步骤4）中得到的k个近邻训练样本点进行统计，计算k个训练样本点每个类别所占的个数，把测试样本的类别归为所占个数最多的训练样本所属的类别。

2 卡方距离度量

选择不同的距离计算方式会对KNN算法的分类准确率产生直接的影响，传统的KNN算法使用欧氏距离作为距离的度量，欧氏距离的度量方式只考虑各个特征量绝对距离，往往忽视各特征量的相对距离。分类中相对距离更加具有实际意义，卡方距离能有效反应各特征量的相对距离变化，同时根据每个特征量对分类贡献的不同，结合灵敏度法计算卡方距离下的特征量的权重。

2.1 卡方距离模型

卡方距离是根据卡方统计量得出的，卡方距离已经被应用到很多的距离描述问题，并且取得相当好的效果。卡方距离公式为

2.2 卡方距离与二次卡方距离的关系

2个直方图统计量X、Y是非负值而且有界限的，则2个直方图距离的二次式距离公式为

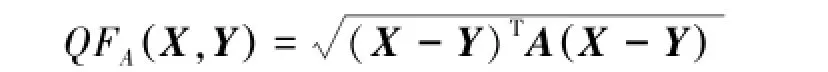
如果矩阵A是协方差矩阵的逆，该二次式距离就是马氏距离。如A是单位矩阵，二次式距离就是欧氏距离。QC代表二次卡方距离。而二次卡方距离［10］公式为

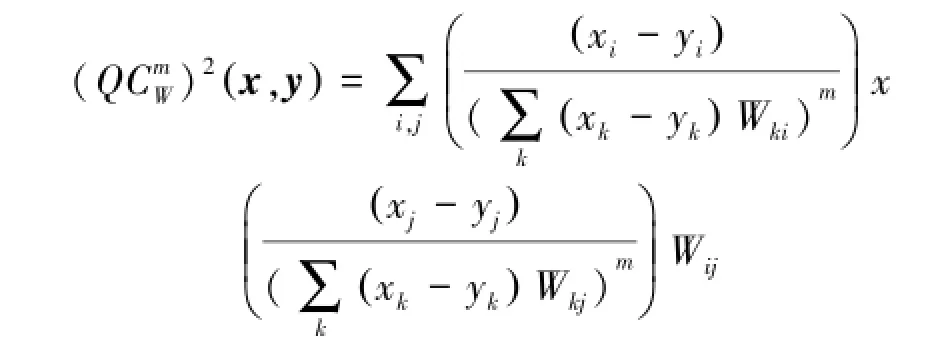
实际上二次卡方距离是二次式距离的标准形式，当m＝0.5，W是单位矩阵时，此时的QC距离是卡方距离，其形式为

当m＝0，二次卡方距离就是二次式距离。由此可见卡方距离和欧氏距离、马氏距离一样可以对特征向量进行有效的度量。

2.3 权重调整系数的计算方法

卡方距离体现了特征量之间的相对关系，但是仍然对每个特征量赋予相同的权重，实际情况是不同特征对分类的贡献不同，因此，本文在卡方距离的基础上采用灵敏度法对不同的特征赋予不同的权重。特征权重的计算方法如下：

1）用卡方距离代替欧氏距离对测试样本进行分类，统计分类错误的样本个数n。

4）第q个特征量的权重系数定义为

3 基于卡方距离的改进KNN算法

本文在传统的KNN的基础上，采用卡方距离度量学习、应用灵敏度法计算不同特征的权重，应用新的距离度量函数代替欧式距离进行度量，得到基于卡方距离的KNN（CSKNN）算法。

3.1 CSKNN算法基本流程

算法流程图如图1所示，基本流程如下。

1）创建测试样本集和训练样本集，训练样本集表示为X，测试样本集表示为Y。

2）给k设定一个初值。

3）计算测试样本点和每个训练样本点的加权卡方距离。公式如下所示：

4）在步骤3）所得的距离按照降序排列，选择离测试样本点较近的k个训练样本。

5）统计步骤4）中得到的k个近邻训练样本点所属的类别，把测试样本的类别归为k个训练样本点中出现次数最多的类别。

6）根据分类结果，评价其查全率R、查准率P、F1宏值以及分类精度，判断分类效果是否达最好，若是，则结束；若否，返回步骤2）对k值进行调整。

图1 算法流程图

3.2 实验结果及分析

实验采用MATLAB R2010a软件进行仿真，在Intel（R）Celeron（R）CPU 2.60GHz，2 GB内存，Windows 7系统的计算机上运行。采用3组数据集进行实验来验证算法分类的有效性，3组数据集来自用于机器学习的UCI数据库，表1给出了3组数据集的基本信息。

表1 实验用到的UCI数据集

对分类算法进行评价指标分为宏平均指标和微平均指标，宏平均指标体现的是对类平均情况的评价，微平均则更加注重对样本平均情况的评价。为了对比本文算法和传统KNN算法的性能，采用分类性能评价指标为宏平均查全率(R)、宏平均查准率(P )和F1测量值，同时分类精度(C)也是评价分类方法的重要指标。

查全率公式为

式中：A表示分类正确的样本数，B表示测试样本的总数。

在实验中本文选择数据集的1／3作为训练样本，数据集的2／3作为测试样本。在k＝5时，实验结果如表2所示；在k＝8时实验结果如表3所示。

表2 k＝5时3组UCI数据集实验对比结果

表3 k＝8时3组UCI数据集实验对比结果

从表2中可以看出，当k＝5时，在Iris数据集上，改进算法的查全率、查准率和F1值都增加约2%。在Haberman数据集上，改进算法的查全率增加了2.3%、但是在查准率和F1值上低于传统的KNN算法。在Pima-India diabetes数据集上，相比于传统算法查全率增加了4.3%，查准率增加了7.8%，F1值增加了8%。从表3的实验对比结果容易得出，当k＝8时，在Iris数据集上，改进算法的查全率增加了2.5%、查准率增加了3.1%、F1值增加了3.1%。在Haberman数据集上，改进算法的查全率上增加了9.2%、查准率和F1值分别增加了5.2%和5.9%。在Pima-India diabetes数据集上，相比于传统算法，查全率增加了2.8%，查准率增加了4.7%，F1值增加了4.5%。

通过分析表2、3可知，当k＝5时，除在Haber-man数据集上的查准率和F1值低于传统KNN算法，在其他数据集上改进的KNN算法的各项指标均高于传统的KNN算法。而当k＝8时，改进的KNN算法的各项指标均明显优于传统的KNN算法

分类精度也是评价分类效果的重要指标，k的取值对分类精度的影响非常明显，k的取值过小，从训练样本中得到信息相对较小，分类精度就会下降；但是k也不能过大，这是因为选择了太多的近邻样本，对从训练样本中得到的分类信息造成大的干扰。因此在选取k值的时候，就不得不做出某种折中。

为了说明k值对分类精度造成的影响，本文选取k＝3、5、8、10、12、15时，在3组UCI数据集上进行测试，得到分类精度随k值变化曲线。Iris数据集的分类准确度随k值得变化曲线如图2所示。Haberman数据集的分类准确度随k值得变化曲线如图3所示。Pima-India diabetes数据集的分类准确度随k值得变化曲线如图4所示。

图2 Iris数据集分类精度随k值变化曲线

图3 Haberman数据集分类精度随k值变化曲线

图4 Pima-India diabetes数据集分类精度随k值变化曲线

分析图2～4可知，分类精度随着k值的不同而发生变化，改进的算法和传统的算法在分类精度达到最大时的k值并不相同，对不同的数据集分类精度达到最大时k值也可能不相同，Haberman数据集上在k＝3、5时改进的KNN算法分类精度低于传统的KNN算法，在k取其他值时分类精度明显高于传统算法，在Iris和Pima-India diabetes数据集上分类精度明显得到提高。

4 结束语

介绍了基于卡方距离的改进KNN算法，用特征权重调整系数的卡方距离代替欧氏距离作为距离度量，克服了欧氏距离对每个特征量赋予相同权重的缺点。通过MATLAB仿真分析验证了改进算法在查全率、查准率、F1值以及分类精度上得到了提高，尽管k值没有一个统一的确定方法，但是在相同k值的条件下，改进KNN算法的分类效果明显高于传统的KNN算法。

［1］奉国和.自动文本分类技术研究［J］.情报杂志，2004，2（4）：108-111.

［2］COVER TM，HARTP E.Nearest neighbor pattern classifi-cation［J］.IEEE Transactions on Information Theory，1967，13（1）：21-27.

［3］LI J.TKNN：an improved KNN algorithm based on tree structure［C］//Seventh International IEEE Conference on Computational Intelligence and Security.Sanya，China，2011：1390-1394.

［4］彭凯，汪伟，杨煜普.基于余弦距离度量学习的伪K近邻文本分类算法［J］.计算机工程与设计，2013，34（6）：2200-2203.

［5］LIM H.An improve KNN learning based Korean text classifi-er with heuristic information［C］//The 9thInternational Conference on Neural Information Processing.Singapore，2002：731-735

［6］桑应宾.一种基于特征加权的K-Nearest-Neighbor算法［J］.海南大学学报，2008，26（4）：352-355.

［7］WEINBERGER K Q，SAUL L K.Distancemetric learning for large margin nearest neighbor classification［J］.The Journal of Machine Learning Research，2009（10）：207-244.

［8］KEDEM D，TYREE S，WEINBERGER K Q，et al.Non-lin-ear metric learning［C］//Neural Information Processing Systems Foundation.Lake Tahoe，USA，2012：2582-2590.

［9］苏金树，张博锋，徐昕.基于机器学习的文本分类技术研究进展［J］.软件学报，2006，17（9）：1848-1859.

［10］PELE O，WERMAN M.The quadratic-Chi histogram dis-tance family［C］//The 11thEuropean Conference on Com-puter Vision.Crete，Greece，2010：749-762.

An improved KNN algorithm based on Chi-square distancemeasure

XIE Hong，ZHAO Hongye
College of Information and Communication Engineering，Harbin Engineering University，Harbin 150001，China

The K-nearest neighbor（KNN）algorithm is one of the classification algorithms，and it isobvious in clas-sification effect，is simple and can be grasped easily.One of themost significant factorswhich determine the effect of the K-nearestneighbor classification is distancemeasure.Euclidean distance isusually considered as themeasure function of the K-nearest neighbor algorithm，it assigns the same weight to different characteristics of the samples，but different characteristic parameter has different influence on the accuracy of the classification results.This paper adopts Chi-square distance which canmore reflect the relative relationship between characteristics asmeasure func-tion of KNN algorithm and uses sensitivitymethod to compute the characteristic weight，so as to overcome the short-coming of Euclidean distance.The result of classification test shows evaluation indexes of the improved algorithm based on Chi-square distance are better than the traditional KNN algorithm.

K-nearestneighbor algorithm；Chi-square distance；distancemeasure；quadratic-form distance；Euclid-ean distance；sensitivitymethod

TP391.4

：A

：1009-671X（2015）01-010-05

10.3969／j.issn.1009-671X.201401002

http：//www.cnki.net／kcms／detail／23.1191.U.20150112.1433.001.htm l

2014-01-06.

日期：2015-01-12.

黑龙江省自然科学基金资助项目（F201339）.

赵洪野（1992-），男，硕士研究生；谢红（1962-），女，教授，博士生导师.

谢红，E-mail：xiehong＠hrbeu.edu.cn.