机械搅拌反应器内气体分布的数值模拟

宋 涛，蒋开喜，周俊武,3，冯昱清

（1.东北大学 材料与冶金学院，辽宁沈阳110819；2.北京矿冶研究总院，北京市100160；3.矿冶过程自动控制技术北京市重点实验室，北京市102628；4.CSIRO Mineral Resource Flagship,Clayton VIC 3168,Australia）

机械搅拌反应器内气体分布的数值模拟

宋 涛1,2,3，蒋开喜2，周俊武2,3，冯昱清4

（1.东北大学 材料与冶金学院，辽宁沈阳110819；2.北京矿冶研究总院，北京市100160；3.矿冶过程自动控制技术北京市重点实验室，北京市102628；4.CSIRO Mineral Resource Flagship,Clayton VIC 3168,Australia）

机械搅拌反应器内通常包含气、液、固等多相体系，利用计算流体力学方法针对其内部复杂物料运动的模拟近年来取得了很大进展。欧拉双流体模型被用来模拟一种装配Rushton型叶轮机械搅拌反应器内包含气泡的气液两相流，并通过不同的相间力模型及自定义湍流子模型描述槽内气泡复杂运动。分析了不同曳力、气泡诱导湍流、升力、湍流分散力等模型在模拟气泡分布时的效果，并将模拟结果与Barigou和Greaves的试验结果进行比较。结果表明，提出的模拟方法在机械搅拌反应器模拟中能够得到准确的气体分布结果。

机械搅拌反应器；气泡流；气液两相流；数值模拟

机械搅拌反应器广泛应用于矿物加工、湿法冶金、化工工业、食品工业、废水处理等过程工业。反应器内通常包含气、液、固等多相体系，各相之间的混合交互也在一定程度上影响着槽内流场。近年来使用计算流体力学方法对机械搅拌反应器内多相流场的研究发展很快，该方法在投入较少的情况下能获得较完备的流场信息，成为进行设备设计和优化的有力工具。

许多学者使用欧拉—欧拉方法进行机械搅拌反应器内气液两相流的模拟，并取得了不错的结果[1-3]。通常情况下,曳力对气泡在反应器内的运动影响很大[4]。常用的几种曳力模型基本上来源于单个气泡在静止液体中的运动,对于类似于机械搅拌反应器内的湍流环境能否适用还需要探讨[5]。Ishii和Zuber[6]提出的曳力系数模型,主要考虑不同气泡直径下气泡运动形状和气泡簇效应对气泡终端速度的影响,但没有考虑湍流环境对气泡运动的影响。Pinelli等[7]通过对小颗粒在湍流环境中的运动总结得到湍流环境中颗粒终端速度变化规律,得到相关曳力模型,并且独立于叶轮样式,反应器尺寸和液体黏度。Fajner等[8]则是在Pinelli等的基础上考虑了相间密度差的影响,并重新修正了式中参数。尽管Pinelli模型和Fajner模型一般用于颗粒在湍流环境中运动的计算,但在机械搅拌反应器中的湍流环境中,尺寸小的气泡与颗粒运动状态类似，可以考虑采用此种模型进行气泡运动的模拟。另外,在存在大量气泡的情况下,气泡对液相流场的影响也不应该忽视。气泡运动带来的液相湍流脉动可称作气泡诱导湍流,一些气泡诱导湍流模型在机械搅拌反应器内气液流场模拟中的表现值得关注。其他气泡与液相之间的相互作用力,例如升力、湍流分散力对气体分布的模拟结果影响也很大，如何在机械搅拌反应器内混合环境中使用也需要进行试验。

本文使用欧拉双流体模型模拟了一种机械搅拌反应器内的气液流场和气体分布。对比了3种不同曳力系数模型的计算效果,找到适合搅拌环境中气泡运动的曳力系数模型;并通过数值试验的方法对比了几种气泡诱导湍流、升力和湍流分散力对气体分布模拟结果的影响。通过模拟结果与Barigou和Greaves[9]的试验值的比较,确定了较为准确的机械搅拌反应器内气液两相流模拟模型。

1 模型描述

1.1 控制方程

对于机械搅拌反应器槽内气液两相流系统，采用欧拉双流体模型进行描述。在不考虑气泡与液相之间的质量与热量传递时，气相和液相运动分别由以下时均质量和动量守恒方程控制[10]（α=l时为液相控制方程，α=g时为气相控制方程）。

式中：rα为各相的体积分数，ρα为各相密度，t为时间，Uα为各相平均速度矢量，ρα为各相压力。Fα相间动量传递，包括曳力、升力、虚拟质量力、壁面润滑力和湍流分散力等。这里的μeff为等效黏度，可以认为是分子黏度与湍流黏度的和的形式，即μeff=μo+μtα。湍流黏度μtα=C1ραkα2/εα，k，ε分别为湍动能和湍流耗散率，C1为k-ε湍流模型常数，取0.09。对于气相采用零方程模型描述湍流，对于液相采用k-ε两方程模型描述。

1.2 曳力

曳力是由气泡周围液体施加在其上，并对加速上升的气泡产生相反方向阻碍的力。在机械搅拌反应器内气液两相流模拟中，曳力（FD）可以看作是决定气体分布的最主要因素。其可以写作以下形式：

式中：dg为气泡直径,CD为曳力系数。曳力系数依赖于流体性质、气泡直径、重力以及气液相界面间的污染程度[11]。

Ishii和Zuber针对完全杂质水环境下的气泡、颗粒、液滴的运动规律提出的曳力系数模型考虑了气泡形状和气泡间相互作用的因素,使用分段模型的方式描述不同气泡的终端速度。

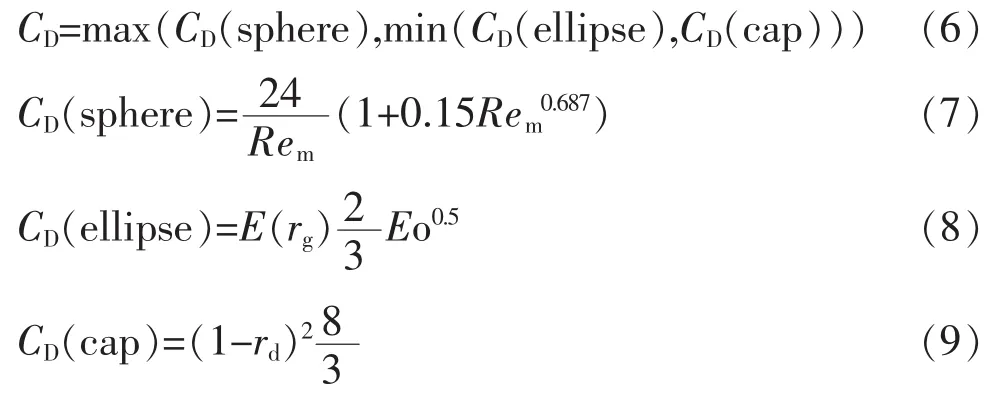
式中:UT为静止液体环境下气泡的终端速度。Mendelson[12]提出了纯水中1.3 mm至15 mm气泡终端速度的计算公式：

式中:sphere、ellipse、cap分别代表小直径、中等直径和较大直径不同形状气泡的曳力系数。Rem为修正的气泡雷诺数，E(rg)和(1-rd)2为反映多气泡环境下气泡间相互作用对曳力系数影响函数。

依据静止液体中气泡的受力平衡，曳力系数模型可以用以下形式表示：

式中:σ为液体表面张力系数。

为了考虑湍流环境对气泡终端速度的影响，Pinelli等在一种稀释溶液的湍流环境中建立了湍流环境中的颗粒终端速度（US）与静止液体环境中颗粒终端速度（UT）的经验关系式：

式中:λ/dg为Kolmogorov微尺度长度λ=(v3/ε)0.25（v为液相运动黏度）与气泡直径的比值。使用US代替公式（10）中的UT，即可计算湍流环境下的曳力系数。

Fajner等在Pinelli等研究的基础上对模型进行了修改，并在颗粒分布模拟中取得了较好的效果：

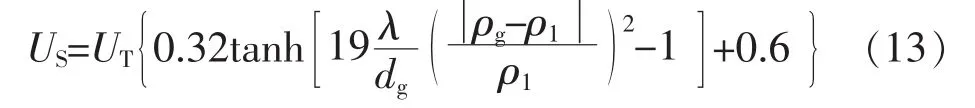
虽然Pinelli等和Fajner等提出的曳力计算模型原用来模拟搅拌系统中颗粒运动，许多学者使用类似的模型较好地模拟了在湍流环境下的气泡运动分布。所以本文也测试了这些模型对机械搅拌式反应器内气液流场的模拟效果。

1.3 气泡诱导湍流

Kataoka和Serizawa[13]认为在包含气泡的气液两相流模拟中，液相流体会受到气泡运动的影响，如果仅仅使用通过单相液体运动特性得到的湍流模型，不能够准确预测流场内液相湍流信息。需要考虑在单相流湍流模型的基础上加入气泡诱导湍流。宋涛等[14]曾在气升式环流反应器气液两相流模拟中使用向k和ε的守恒方程中添加源项的方法，来描述气泡诱导湍流所引起的湍动能的对流和扩散现象，并取得了较好的模拟效果。本文也尝试将此模型用于机械搅拌反应器内气液两相流的模拟，分别在k-ε湍流方程中添加以下源项：

式中:Ck和Cε为可调整的系数，这里都取1。

Sato和Sekoguchi[15]提出的模型，通过将湍流应力张量中的等效黏度分为剪切诱导项和气泡诱导项的方法进行模拟：

式中:μ1,SI=μtl为剪切诱导黏度，μ1，BI为气泡诱导黏度。本文也将考察此模型在机械搅拌反应器内气液两相流模拟中的效果。

1.4 升力

升力描述的是气泡与液相剪切场之间的相互作用，是气泡在上升过程中水平方向运动的决定因素之一。在气液两相流模拟中，升力模型的选取往往会对计算结果造成较大影响。单位体积升力（FL）的计算公式为：

式中:CL为升力系数。这里考虑考察两种升力模型。式(19)为使用固定的升力系数；式(20)则按照Tomiyama[16]提出的基于单气泡的升力系数模型进行计算。

1.5 湍流分散力

湍流分散力是由湍流涡动和相间曳力共同作用的结果。有些气泡在上升过程中会被湍流涡捕获,并由相间曳力从高浓度区域输送到低浓度区域。

Lopez模型是最早提出的湍流分散力模型之一，其表达式如下[17]：

湍流分散力系数CTD取值在0.1到0.5之间的模型应用于小直径气泡运动模拟时效果较好。

Burns等[18]给出了在欧拉两相流体系下的湍流分散力（FTD）的一般形式（Favre Averaged Drag Model）：

式中:湍流分散力系数CTD取值为1；CD为相间曳力系数；νt1为液相运动黏度；σt1为湍流施密特数，此处取值0.9。

1.6 模型实现

本文反应器几何模型使用与Barigou和Greaves相同的机械搅拌反应器，两相介质分别为空气和水。该反应器为平底反应器，高度和直径都为1 m。在桶壁四周均匀分布4个挡板，挡板宽度为0.1 m。反应器搅拌系统为直径0.33 m的标准Rushton叶轮，叶轮距底面0.25 m。充气装置位于叶轮正下方槽底中心处，为直径19 mm的圆形充气孔。操作条件分别为充气量Qg=0.001 64 m3/s，叶轮转速180 rpm和充气量Qg=0.006 87 m3/s，叶轮转速285 rpm。为了节省计算时间，这里假设槽内流场对称，建立了完整搅拌槽的1/2区域，两个挡板和三片叶轮以反应器的中心截面为对称。气泡直径使用试验中观察的平均值2 mm。模拟试验采用的网格数为223 393，并利用网格数为343 533的模型做网格无关性试验。具体网格结构如图1所示。使用多重参考坐标系法模拟叶轮的旋转，即叶轮区域在旋转坐标系下计算，外层带有挡板的区域使用静止坐标系。控制方程使用ANSYS CFX 14.5进行求解，采用自定义子模型的方式对相间力和气泡诱导湍流进行描述。中心对称面设置为旋转循环界面。模型出口使用一种对于气相为压力出口，对于液相为壁面的边界条件。

图1 几何模型及网格划分

2 结果与讨论

模拟计算分别在不同的操作条件下进行,以涵盖不同充气量及叶轮转速条件下装备Rushton叶轮的机械搅拌反应器内的气液流场。计算结果与Barigou和Greaves试验中得到的气体体积分数值进行比较,从而考察不同子模型的计算效果。

曳力系数模型决定气泡在液体中所受阻力的大小,所以也决定着气泡在液相中的终端速度。合适的曳力系数模型能够改进模拟中气泡在反应器内的分布。在进行模拟实验之前，首先利用不同的曳力系数模型计算重力环境下单个气泡在液体中的气泡终端速度,以观察不同曳力模型所计算的气泡速度的区别。图2是在分别使用Ishii&Zuber模型、Fajner模型和Pinelli模型计算的不同直径气泡的终端速度。

图2 水中不同曳力系数模型下气泡终端速度与气泡直径之间的关系

图2中可以看出2 mm直径气泡在使用Ishii& Zuber模型计算曳力系数时所获得的终端速度最大, Fajner模型得到的2 mm气泡终端速度要小很多,而Pinelli模型计算得到的2 mm气泡终端速度最小。显然依据Fajner模型和Pinelli模型,湍流环境下单气泡终端速度要小于静止流体中单气泡终端速度。

表1是在使用三种不同曳力系数模型时槽内充气量模拟值与试验值的比较。从对比结果可以看出,使用Ishii&Zuber模型时得到的槽内气体体积分数最小,同时在两种操作条件下都与试验值有较大差别，严重低估了槽内气体体积分数。使用Fajner模型时，气体体积分数预测值有了较大改善，接近试验值，但在两种操作条件下都较试验值小一些。使用Pinelli模型时，在较高充气量条件下，气体体积分数模型预测值要比试验值高约9.3%，而在较低充气量条件下预测值在几种模型中最接近试验值，但依然小于试验值。

表1 不同曳力模型预测值与Barigou和Greaves试验值[9]的比较

为了进一步改进模型对气体分布的模拟效果，这里还尝试使用了不同气泡诱导湍流模型，升力模型和湍流分散力模型。表2为使用不同模型时气体体积分数预测值与Barigou和Greaves试验值的比较，所有的模型均使用Fajner模型计算曳力系数。

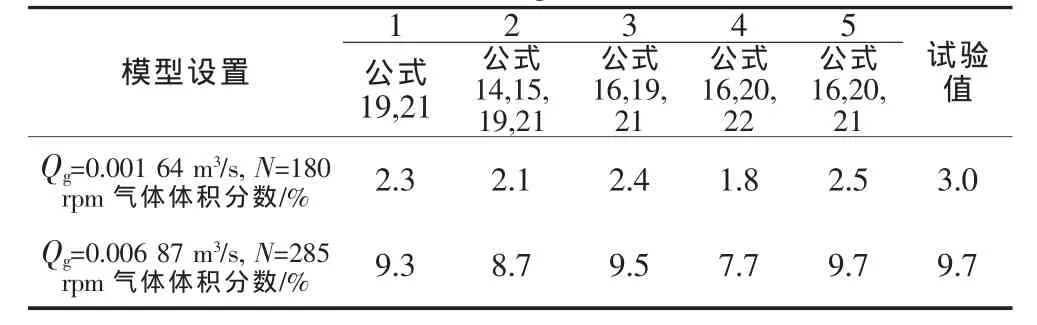
表2 不同模拟模型预测值与Barigou和Greaves试验值[9]的比较

表2模型1使用固定升力系数0.5和系数为0.1的Lopez湍流分散力模型。Zadghaffari和Moghaddas[19]曾使用此模型计算Rushton叶轮搅拌槽中的气体分布并取得较好结果。对比结果显示,在两种充气量条件下气体体积分数预测值都较试验值稍小。模型2在模型1的基础上增加宋涛等使用的气泡诱导湍流模型，得到的气体体积分数预测值较模型1减小，此模型在机械搅拌反应器气液两相流模拟中效果并不理想。模型3考虑使用Sato和Sekoguchi提出的气泡诱导湍流模型，计算结果较模型1有所改进，预测值更加接近试验值。模型4在模型3的基础上增加Tomiyama升力模型和Burns等提出的湍流分散力模型，计算结果显示使用Burns湍流分散力模型大大降低了槽内气体体积分数，效果并不理想。模型5使用Sato和Sekoguchi提出的气泡诱导湍流模型，Tomiyama升力模型，Lopez湍流分散力模型（系数调整为0.25），由计算结果看出预测槽内气体体积分数值在两种操作条件下都与试验值很接近，尤其是在较高充气量条件下。

使用模型5时,充气量Qg=0.006 87 m3/s,叶轮转速285 rpm条件下,模型预测的液相流速矢量分布及气体体积分数分别如图3和图4所示。由图3的模拟结果可以看出，液相流场的高速区分别位于充气口上方以及叶轮四周向壁面辐射的区域,并形成以叶轮平面为分界的上下两个循环流场。充气量Qg=0.001 64 m3/s,叶轮转速180 rpm时,槽内液相流场分布与图3类似。槽内中心截面处气体体积分数分布如图4所示。由模拟结果看出,充气口进入搅拌槽的气体被叶轮分散到槽内四周,在槽内流场形成的两个循环区域中心处,气体体积分数值较高,终端速度较小的气泡会聚集在这些区域。

图3 槽内中心截面处液相速度矢量分布(充气量Qg=0.006 87 m3/s，叶轮转速285 rpm)

图4 槽内中心截面处气体体积分数分布(充气量Qg=0.006 87 m3/s，叶轮转速285 rpm)

通过比较不同曳力模型的模拟效果，Ishii& Zuber模型在使用实验观察平均气泡直径时并不能准确模拟机械搅拌环境下气泡在槽内的分布，而通过固体小颗粒试验得到的曳力系数模型则能较为准确地预测气体体积分数值。而合适的气泡诱导湍流模型，升力模型以及湍流分散力模型能够很好地补充湍流环境，多气泡间相互作用对气泡运动带来的影响，修正气泡分布的预测值，取得较好的模拟效果。

3 结论

本文使用欧拉双流体模型模拟了一种实验室机械搅拌反应器内的气液流场和气体分布。通过比较不同的曳力系数模型，不同的气泡诱导湍流、升力和湍流分散力模型的模拟效果，考察了这些模型在气体分布模拟计算中的作用。通过这些模型模拟值与Barigou和Greaves试验值的对比，提出一种能够准确预测反应器内气体分布的模拟模型。本文模拟模型可以为机械搅拌反应器内气液两相流模拟模型的建立提供参考依据，并在大型工业搅拌槽、浮选机等搅拌设备的放大过程中，提供相关的理论支持。

[1] Wang Weijing,Mao Zaisha.Numerical Simulation of Gas-Liquid Flow in a Stirred Tank with a Rushton Impeller[J].Chinese J. Chem.Eng.,2002,10(4):385-395.

[2] Lane G L,Schwarz M P,Evans G M.Numerical modelling of gasliquid flow in stirred tanks[J].Chemical Engineering Science, 2005,60(8-9):2203-2214.

[3] Scargiali F,D'Orazio A,Grisafi F,Brucato A.Modelling and simulation of gas-liquid hydrodynamics in mechanically stirred tanks[J].Chemical Engineering Research and Design,2007,85(5): 637-646.

[4] Sokolichin A,Eigenberger G,Lapin A.Simulation of buoyancy driven bubbly flow established simplifications and open questions [J].AIChE Journal,2004,50(1):24-45.

[5] Bakker A,Van den Akker H E A.A computational model for the gas-liquid flow in stirred reactors[J].Chemical Engineering Research and Design,1994,72(A4):594-606.

[6] Ishii M,Zuber N.Drag coefficient and relative velocity in bubbly, droplet or particulate flows[J].AIChE Journal,1979,25(5):843-855.

[7] Pinelli D,Nocentini M,Magelli F.Solids distribution in stirred slurry reactors:influence of some mixer configurations and limits to the applicability of a simple model for predictions[J].Chemical Engineering Communications,2001,188(1):91-107.

[8] Fajner D,Pinelli D,Ghadge R S,Montante G,Paglianti A,Magelli F.Solids distribution and rising velocity of buoyant solid particlesin a vessel stirred with multiple impellers[J].Chemical Engineering Science,2008,63(24):5876-5882.

[9] Barigou M,Greaves M.Bubble-size distributions in a mechanically agitated gas-liquid contactor[J].Chemical Engineering Science, 1992,47(8):2009-2025.

[10] Luo H-P,Al-Dahhan M H.Verification and validation of CFD simulation for local flow dynamics in a draft tube airlift bioreactor [J].Chemical Engineering Science,2011,66(5):907-923.

[11] Tomiyama A,Kataoka I,Zun I,et al.Drag coefficients of single bubbles under normal and micro gravity conditions[J].JSME International Journal Series B,1998,41(2):472-479.

[12] Mendelson H D.The prediction of bubble terminal velocities from wave theory[J].AIChE Journal,1967,13(2):250-253.

[13] Kataoka I,Serizawa A.Basic Equations of turbulence in gasliquid two-phase flow [J].International Journal of Multiphase Flow,1989,15(5):843-855.

[14] 宋涛，蒋开喜，周俊武，等.气升式环流反应器内气泡分布的数值模拟[J].矿冶，2015，24(1)：61-66.

[15] Sato Y,Sekoguchi K.Liquid velocity distribution in two-phase bubble flow[J].International Journal of Multiphase Flow,1975,2 (1):79-95.

[16] Tomiyama A.Struggle with computational bubble dynamics[J]. Multiphase Science and Technology,1998,10(4):369-405.

[17] Lopez de Bertodano M A.Two fluid model for two-phase turbulent jets[J].Nuclear Engineering and Design,1998,179(1): 65-74.

[18] Burns A D,Frank T,Hamill I,et al.The favre averaged drag model for turbulence dispersion in Eulerian multi-phase flows[C] //Proceedings of 5th International Conference on Multiphase Flow.Yokohama:ICMF'04,2004:392.

[19] Zadghaffari R,Moghaddas J S.Evaluation of drag force effect on hold-up in a gas-liquid stirred tank reactor[J].Journal of Chemical Engineering of Japan,2010,43(10):833-840.

Numerical Simulation OF Gas DIstribution In a Stirred Tank Reactor

SONG Tao1,2,3,JIANG Kaixi2,ZHOU Junwu2,3,FENG Yuqing4
(1.School of Materials and Metallurgy,Northeastern University,Shenyang 110819,China; 2.Beijing General Research Institute of Mining and Metallurgy,Beijing 100160,China; 3.Beijing Key Laboratory of Automation of Mining and Metallurgy Process,Beijing 102628,China; 4.CSIRO Mineral Resource Flagship,Clayton VIC 3168,Australia)

Computational fluid dynamics(CFD)contributes a lot in calculations of complicated multi-phase flows in mechanically stirred reactors.To predict the performance of a tank reactor stirred by Rushton turbine,the Eulerian-Eulerian two-fluid method was used for modeling gas-liquid flow in tank,and extra user defined subroutines were incorporated to consider the complex physics. Different modeling methods of drag force,bubble induced turbulence,lift and turbulent dispersion forces were evaluated in the numerical simulations of the bubble distribution in the reactor.The simulation results have been compared with the experimental measurements of Barigou and Greaves.Some reasonable agreements have been obtained both in flow structures and gas distribution.

stirred tank reactor;bubbly flow;gas-liquid flow;numerical simulation

TF351.5+2

A

1004-4345(2015)03-0022-05

2015-04-01

十二五“863”项目《大型微生物冶金生物反应器》(2012AA061503)。

宋涛（1983—），男，东北大学博士研究生，主要从事矿冶设备、流程建模仿真研究。