中考数学二轮复习中讲题的几点思考

【摘 要】中考数学复习般分三轮进行。其中第二轮复习尤其强调以能力提升为目标。复习一般采用专题形式，以学生掌握的知识、形成的技能、积累的基本活动经验和形成的数学思想方法为基础，以提升学生分析问题、解决问题的能力和培养学生的创造性思维能力。对于案例分析类问题，要引导学生抓住题干关键词;对于问题求解，要探求解法的多样性;对于变式性问题，要在变式层次性上做好铺垫，从而提高学生的复习质量。

【关键词】中考数学;二轮复习;案例分析;问题求解

【中图分类号】G633.6 【文献标识码】A 【文章编号】1005-6009（2015）06-0030-03

【作者简介】杨云奎，江苏省灌云县实验中学（江苏灌云，222200）教师，中学高级教师。

一、讲案例分析时，抓住题干关键词

在中考二轮专题复习中，很多题目题干较长，题中彼此之间的关系相对分散，隐含在字里行间的信息不易“汇聚”。有相当一部分学生在通读一遍题目后，抓不住重点，便失去耐心选择放弃。因此教师在对这类问题进行分析时，要给学生留有一定的时间，给学生“理解”题干的空间，让学生有一个“悟”的过程。还要让学生解释文本中的“关键词”，教师针对学生的解释要作必要的追问和阐释，以帮助学生准确理解题意，为顺利解题打下坚实的基础。

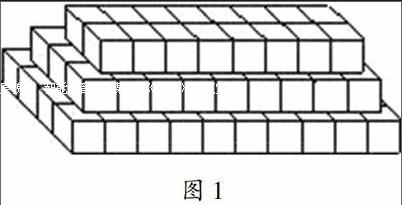
【案例1】探索、研究。仪器箱按如图1方式堆放（自下而上依次为第1层、第2层…），受堆放条件限制，堆放时应符合下列条件：每层堆放仪器箱的个数an与层数n之间满足关系式an=n2-32n+247，1≤n<16，n为整数。

（1）例如，当n=2时，a2=22-32×2+247=187，则a5 = ，a6 = 。

（2）第n层比第（n+1）层多堆放多少个仪器箱（用含n的代数式表示）;

（3）如果不考虑仪器箱堆放所承受的压力，请根据题设条件判断仪器箱最多可以堆放几层，并 说明理由;

（4）设每个仪器箱重54N，每个仪器箱能承受的最大压力为160N，并且堆放时每个仪器箱承受的压力是均匀的。

①若仪器箱仅堆放第1、2两层，求第1层中每个仪器箱承受的平均压力;

②根据①中的方法进行估算，求得最多可以堆放的层数。在确保仪器箱不被损坏的情况下，仪器箱最多可以堆放几层？为什么？

图1

在本案例中，关键点是对关系式an=n2-32n+247的理解。根据1≤n<16，n为整数，n的取值学生是清楚的，对不同的n，式子n2-32n+247的值也是可求的。但对于an学生普遍认识不足，虽然在求一元二次方程的根时，曾用过x1，x2表示方程的根，但对这种含角码的字母认识上仅属于简单模仿阶段，对关系式an=n2-32n+247中an这种含角码的字母的意义理解并不深刻。虽然在第（1）小题中作了铺垫，但仍有学生不能充分认识an中的角码n与关系式右边的n一样，是随n变化的变量。如果教师能对此解读到位，则为顺利解题奠定了基础。

“每个仪器箱承受的压力”是本案例中的又一关键词，教师只需提醒学生注意，一般学生便能明白它的含义：某层以上所有仪器的重量平均分配到这一层所有仪器上。

教师在备课时要找准问题的关键词。在分析题目之前，教师要充分地让学生展示其对关键词的解读。当学生对关键词不解时要作必要的点拨，学生对关键词解读差误时，要及时纠正。紧抓问题中的关键词，才能节省时间，达到事半功倍之效果。

另外还需注意，由于学生的知识结构、思维方式各不相同，一个不起眼的名词、符号都有可能成为某些学生问题求解过程中的绊脚石。教师在施教时也要引起足够的重视。比如以上案例题干中有一说明：“自下而上依次为第1层、第2层…”与我们常规的理解“自上而下依次为第1层、第2层…”恰好相反，若在审题时没有引起足够注意，也会给解题带来困难。

二、讲问题求解时，探求解法多样性

一题多解就是对同一问题，由于解题者观察的角度不同，思考的侧重点不同，运用知识不同和思维力度不同而得到不同的求解方法。一题多解在日常的例题教学中常被教师所采用。不可否认，对学生进行一题多解训练，可以提高解题能力，做到举一反三、触类旁通，有利于培养学生的发散性思维能力。但是，在以提升学生能力为目标的中考第二轮复习中，在进行多途径需求问题解答时不能为了多解而多解，而要力争在解题方法上或思维方式上有所突破，而不是局限在某一类方法中或同一思维层面上。

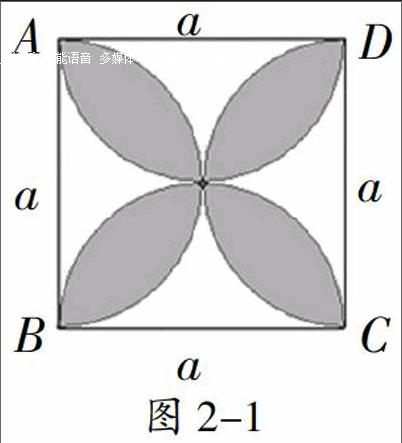
【案例2】如图2-1，正方形ABCD的边长为a，以各边为直径在正方形内作半圆，求图中阴影部分的面积S阴。

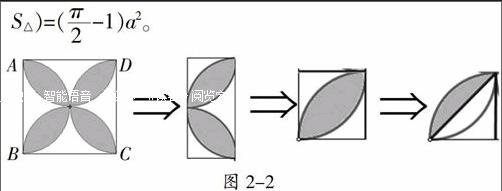
思考一 求含圆弧的封闭图形面积，一般是将圆弧所在圆的圆心与圆弧两个端点相连接，将待求图形面积转化为直线型图形与扇形的面积。本例根据图形的对称性，将原图形按图2-2变化方式，比照变化前、后两个图形的关系，于是有：S阴=8（■S阴-S△）=（■-1）a2。

思考二 如图2-3，由图形的对称性，4个半圆把正方形分割为两类图形，分别用x、y表示其面积，根据面积间的相等关系，通过列方程组求出每类图形的面积：

4x+4y=a22x+y=■π（■）2解得x=■（■-1）a2y=■（2-■）a2，于是4x=（■-1）a2，所以S阴=（■-1）a2。

思考三 如果从图2-1阴影部分的形成过程进行思考，我们认为先是在正方形中把相对的两个半圆染色（如图2-4），显然图中的非阴影部分的面积为（a2-■πa2），于是图2-1非阴影部分面积是2（a2-■πa2），从而S阴=a2-2（a2-■πa2）=（■-1）a2。

以上三种思考从不同的角度分析问题，思考一体现了求含圆弧的封闭图形面积的通用方法;思考二是运用数形结合，将面积问题转化为方程组的求解;思考三则是对图形的阴影部分作了动态思考。尽管我们还可以对图形进行剪拼，借助图形间的面积关系列出方程（组），也可以在思考三的基础上第二次把相对的两个半圆染色进而求出阴影部分的面积，但它们仅是在思考二、三的解法细节上作出的调整，思维方式上并没有真正意义上的突破。在以能力提升为主的二轮复习中，题目多解应是教师引导启发的自然生成，而非多多益善，一切应以揭示问题的本质为要。

三、讲问题变式时，注重变式层次性

一题多变也是在中考二轮复习中教师经常采用的一种行之有效的教学策略，它能在有限的课堂教学时空内让学生“聚焦”现有的教学资源，减少学生的信息接受总量，让学生能有更多的时间观察、分析、思考、探索。常以某一问题为载体，以数学知识、技能或数学方法为基本点，纵向深入，对其进行深度剖析，一题多变给人以新鲜感，能够唤起学生的好奇心和求知欲，有助于培养学生的探究创新能力，提高学生全面掌握知识和灵活运用知识的能力。

【案例3】表1-1是由从1开始的连续自然数组成，观察规律并完成各题的解答。求表中第8行第3个数是 ，表中第20行第14个数是 。

表1-1

变式一 表1-2是由从1开始的连续自然数组成，观察规律并完成各题的解答。求表中第8行第3个数是 ，表中第20行第14个数是 。

表1-2

变式二 表1-3是由从1开始的连续奇数组成，观察规律并完成各题的解答。求表中第8行第3个数是 ，表中第20行第14个数是 。

表1-3

仔细观察表1-1，可以发现第一行有1个数，第二行有3个数，第三行有5个数……于是，第7行有13个数，所以前7行共有数（1+3+…+13）=49个，于是第8行第1个数是50，从而表中第8行第3个数是52。类似地，可以求出第20行第14个数为375。

通过观察，我们还能发现表1-1每行的最后一个数分别是1，2，3，4…的平方数，于是第7行最后一个数是49，所以第8行第1个数是50，从而表中第8行第3个数是52。类似地，可以求出第20行第14个数是375。

表1-2中的求解，只要我们沿着以上思路的前一思路是不难给出正确的答案，但教师不能就此而止，而应该引导学生思考：是否能发现每行最后一个数与行数间的特殊关系？教师适时的一句点拨，激发起学生探索的欲望，对于大多数初中学生来讲还不易发现的关系豁然开朗。

表1-3中的数与行之间的关系比较隐蔽，学生对于第一个填空可能会选择按规律写下去而得到答案，但对于第二空由于时间的限制及书写量太大而大多选择放弃。此时教师提醒学生：观察表1-3与表1-2对应位置各个数有怎样的关系。可谓一句点醒“梦中人”，学生容易发现：表1-3中的数是表1-2中对应位置数的2倍与1的差。此时变式二中待求两数已如“瓮中之鳖”。

一题多变与寻求一题多解一样，也并非变得越多越好。在以“能力立意”的中考二轮复习中，变式问题的设计要能利于引导学生积极探索，最大限度地唤起学生的求知欲。一题多变变在思维水平上，体现渐进性，要利于学生思维的升华，应避免在同一思维水平上变式的反复出现。

中考二轮复习时间紧、任务重、要求高，教师的例题讲解对于提升学生分析问题、解决问题的能力起着至关重要的作用。因此，教师要能够在问题分析时，抓住要害，牵住问题“关键词”，以四两之力，拨动千斤之重。在例题讲解时，教师要尽可能地充分利用例题资源，发挥例题的功用，适时适度地对例题作一题多解或一题多变，不论是选择多解还是多变，都要力戒在同一层面的多解或多变，而要在思维的方式方法上有所突破。唯有如此，学生才能学有所得、学有所思、学有所益，学生的综合能力才能有所提高。在讲解例题的过程中，一定要给学生留有思考的时间，让单位课时例题的量“降下去”，让学生思维的质“升起来”。当然，教学例题的选择也至关重要，教师自己在备课时务必根据课时目标、班级实际对集体备课的选题再度进行改编、完善，做题、研题，切忌“拿来主义”。■