自适应非结构有限元MT二维起伏地形正反演研究

韩骑， 胡祥云*， 程正璞， 杨炳南， 蔡建超， 韦伟

1 中国地质大学地球物理与空间信息学院，地球内部多尺度成像湖北省重点实验室， 武汉 4300742 贵州省地矿局， 贵州铜仁 554300



自适应非结构有限元MT二维起伏地形正反演研究

韩骑1， 胡祥云1*， 程正璞1， 杨炳南2， 蔡建超1， 韦伟1

1 中国地质大学地球物理与空间信息学院，地球内部多尺度成像湖北省重点实验室， 武汉 4300742 贵州省地矿局， 贵州铜仁 554300

在山区进行MT勘探时，用规则网格有限元方法模拟起伏地形会受到限制.本文采用非结构三角网格可以有效地模拟任意二维地质结构，如起伏地形、倾斜岩层和多尺度构造等.正演引入自适应有限元方法，其在网格剖分过程中能根据单元误差自动细化网格，保证了正演结果的精度.将自适应有限元与Occam算法结合，且引用并行处理技术提高正反演计算速度.通过对比两个理论模型，讨论了地形对MT正演响应的影响；其次进行了不同地电模型带地形反演展示了本文算法的正确性和适用性；最后将该方法应用于实测MT数据处理，证明了自适应非结构有限元方法是复杂地形下处理MT数据的有力工具.

大地电磁； 自适应有限元； 地形； 反演

1 引言

大地电磁测深法（MT）是通过天然交变电磁场研究地球模型电性结构的一种地球物理方法.大地电磁测深方法具有较大的穿透深度和分辨能力，它不仅是研究地壳与上地幔深部构造的强有力工具（李冉等，2014；吕庆田等，2011），而且可以结合地震数据（刘彦等，2012；詹艳等，2014）和重磁数据（张交东等，2012）进行综合解释分析，已成为矿产勘查（Hu et al.，2013；陆桂福和吴新刚，2014）、地热资源（Wu et al.，2012；高景宏等，2010）和油气勘探（夏训银等，2012）的有效方法.

地形对大地电磁测深的影响是地球物理工作者难以避免的问题.特别是我国山地区域地形起伏剧烈，大地电磁数据采集受各种因素的限制，当测点布置在山沟时，垂直山体方向受高电阻体对电场的排斥作用的影响；若山体不规则，地形影响更为复杂（张翔等，1999）.有限元方法是模拟MT正演响应的有效手段，许多研究者利用矩形网格（Rodi，1976；陈乐寿，1981；童孝忠等，2009；张昆等，2008）和矩形对分三角网格（Wannamaker et al.，1987；Zyserman et al.，1999；刘小军等，2007；柳建新等，2009）模拟地形正演响应，结果表明地形对TM模式的影响远远大于TE模式（王绪本等，1999），并且视电阻率曲线表现为畸变、静态平移或者二者的混合，没有一定规律可循.但矩形及其对分三角网格对复杂地质结构（起伏地形和交错地层等）模拟能力有限，且上述规则网格在对目标区域进行加密时，其背景区域也会受到不必要细化，增加了计算时间.

近年来许多学者（Key and Weiss，2006；Franke et al.，2007；Li and Key，2007；Li and Pek，2008）采用自适应非结构三角网格有限元方法计算电磁场.非结构三角网格能够真实地模拟各种复杂地质结构，该方法利用Delaunay三角划分原理（Shewchuk，2002）对目标区域进行细密网格剖分，而背景区域则粗糙网格剖分.自适应有限元对计算结果进行误差评估（Ovall，2006），误差较大的单元网格自动细分直至有限元计算结果满足给定的误差范围.自适应非结构有限元方法因其强大的适应性，越来越受到地球物理研究者的青睐，其方法技术也日臻完善.现已成功实现了海洋二维MT正演模拟（Key and Weiss，2006；Franke et al.，2007；赵慧等，2014），海洋2.5D可控源正演模拟（Key and Ovall，2011）.在此基础上，本文采用非结构三角网格剖分、自适应有限元与Occam算法结合的策略来研究陆地MT二维带地形反演.首先讨论了不同地形对MT正演的影响；其次建立3个典型地电模型进行带地形反演，并与平地反演结果进行对比；最后对实测MT数据进行反演并解释.

2 方法原理

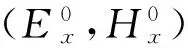
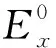
（1）

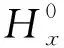
（2）

事先给出一次场对应的电导率为σ0，一次场为均匀半空间模型其电磁场值由解析解算出，二次场则是由σ-σ0的差异引起，采用自适应有限元解出场值，最后将一次场和二次场相加算出总场值.该方法可通过提高二次场解的精度来提高整体解的精度（Rodi，1976），与总场法求解的结果对比验证了该方法的正确性（赵广茂等，2008；刘小军等，2007）.这种方法最大优势在于有限元网格只需要精确地模拟二次场的变化，因此可采用包含更少单元的网格（Key and Ovall，2011），提高计算速度.利用Helmholtz方程得到二次场TE和TM偏微分方程表达式如下：

（3）

（4）

式中ω为角频率，μ=4π×10-7H·m-1为磁导率常数.对研究区域进行三角剖分后生成包含N个顶点的N维向量空间V，式（3）和（4）对应的变分问题可以统一写成：

B（v,u）=F（v）,

（5）

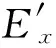
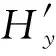
（6）

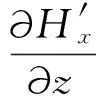
（7）

二次场与一次场相加求得总场值，则MT阻抗为

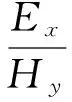
（8）

MT视电阻率和相位角为

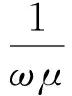
（9）

相对于有限元的解un，解的误差G（u-un）更被研究者重视，其中u是（5）式的真实解，G为误差评估的对偶函数.自适应网格划分的实质是计算出每个三角单元有限元解的误差，对误差较大的三角单元再次细分，直到误差达到允许范围.本文采用对偶加权残差（DWR）法（Ovall，2006）计算单元误差，属于一种后验误差处理技术，通过分级函数对残差进行加权.选择一个合适G函数十分重要，DWR给出了一个比较合适的G函数，单元误差计算过程中多次利用有限元数值方法进行求解，所求误差是逼近真实解的近似值.后验误差方法在工程学领域是一项非常成熟的技术，近几十年被引入到电磁场模拟中，已应用于海洋可控源电磁场（Li and Key，2007；Key and Ovall，2011）、海洋二维MT电磁场 （Franke et al，2007；Key and Weiss，2006；赵慧等，2014）和二维电阻率各向异性介质大地电磁场（Li and Pet，2008）模拟.

反演问题采用Occam算法（Constable et al.，1987），该算法自发表以来由于其稳定性在电磁法反演领域得到了广泛的应用（Ghaedrahmati et al.，2014；Siripunvaraporn and Sarakorn，2011；Sudha et al.，2014；何梅兴等，2011）.Occam反演实质为带光滑约束的最小二乘法，其泛函U表达式为：

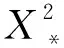
（10）

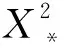
自适应有限元方法进行电磁场数值模拟的主要优势在于可根据每次有限元计算的结果自动进行网格精炼，确保了计算结果的精度，避免了以往正反演过程中网格绘制的繁琐工作，图1给出了自适应有限元与Occam算法结合的计算流程.首先给出反演初始模型作为反演细化的初始网格和电阻率模型参数，一般来说，目标区域网格划分细致，选择小三角单元；背景区域则采用大三角单元.随后进行内存空间分配，即采用多少线程参与计算，每个线程负责多少测点的自适应有限元运算.本文设置单元误差阈值0.02，采用有限元方法计算每个单元的场值，由DWR方法估计单元局部误差，将局部误差大于误差阈值的单元进行细化，得到新的三角网格.重复以上过程直至所有单元误差达到误差阈值或者已达到最大网格细化次数，则网格精炼停止，输出正演结果.设置反演收敛精度1.5，计算数据均方根误差RMS，若未达到反演收敛精度，则更新模型重新开始自适应有限元计算过程直至达到反演收敛精度或者达到最大迭代次数，输出反演结果.

图1 自适应有限元算法反演流程

3 模型计算

3.1 地形对MT响应影响研究

为了研究地形对MT勘探的影响，在100 Ωm的均匀半空间中设置一10 Ωm的矩形低阻体，在图2a中设置包含山谷、山峰起伏地形，最大高差300 m，图2b采用水平地形.从左往右依次设置11个测点，间距300 m，频率范围为0.1～10000 Hz，共22个频点.

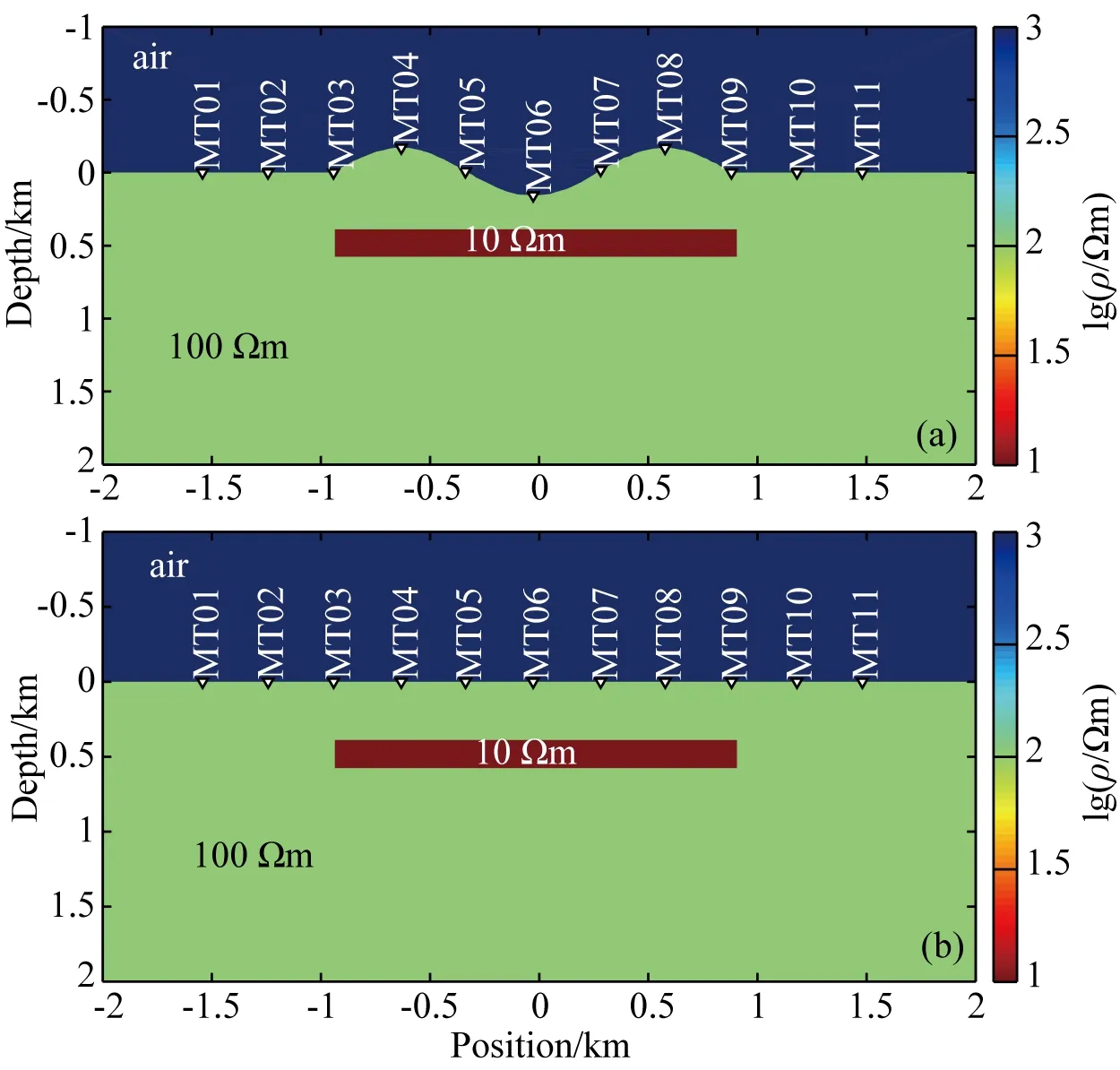
图2 地形影响研究模型

采用自适应有限元方法计算各测点的视电阻率和相位响应值，选取代表典型地形的三个测点MT04、MT05和MT06正演结果进行比较.如图3所示，红色曲线为TM模式，蓝色曲线为TE模式.图3a中TE模式视电阻率和相位曲线相对于平地模型（图3b）波动不大；但是对于TM模式，在山峰处（MT04）视电阻率曲线低频陡然下降，山坡处（MT05）视电阻率曲线整体向上平移，且在高频处上扬，山谷处（MT06）视电阻率曲线高频处上扬.不同地形对正演响应产生的干扰不同，视电阻率曲线会产生畸变、平移或二者的结合，没有十分确切的规律可循，整体来说地形对视电阻率的影响大于相位角，对TM模式的影响远远大于TE模式，推测其原因是两种极化模式中，磁场一般变化平缓，TE模式电场平行于构造走向，TM模式电场垂直走向，垂直于走向的电场会产生感应电场，该感应电场在空间上的分布受地形起伏的影响严重，而在TE模式中只有与走向平行的电场.因此，实现带地形反演消除因地形产生的数据异常十分重要.

3.2 典型地电模型正反演研究

在山区进行MT工作主要以寻找金属矿为目的，金属矿一般呈现低阻性质.如图4所示，在100 Ωm均匀半空间埋藏两个形态不一，埋深不同的10 Ωm的低阻体，1号低阻体中心埋深400 m，呈块状；2号低阻体中心埋深750 m，呈薄板状.测线垂直走向方向分布，全长2000 m，其中包含40个测点，频率范围0.1～10000 Hz，共60个频点，地形采用一组实测高程数据，最大高差达250 m.

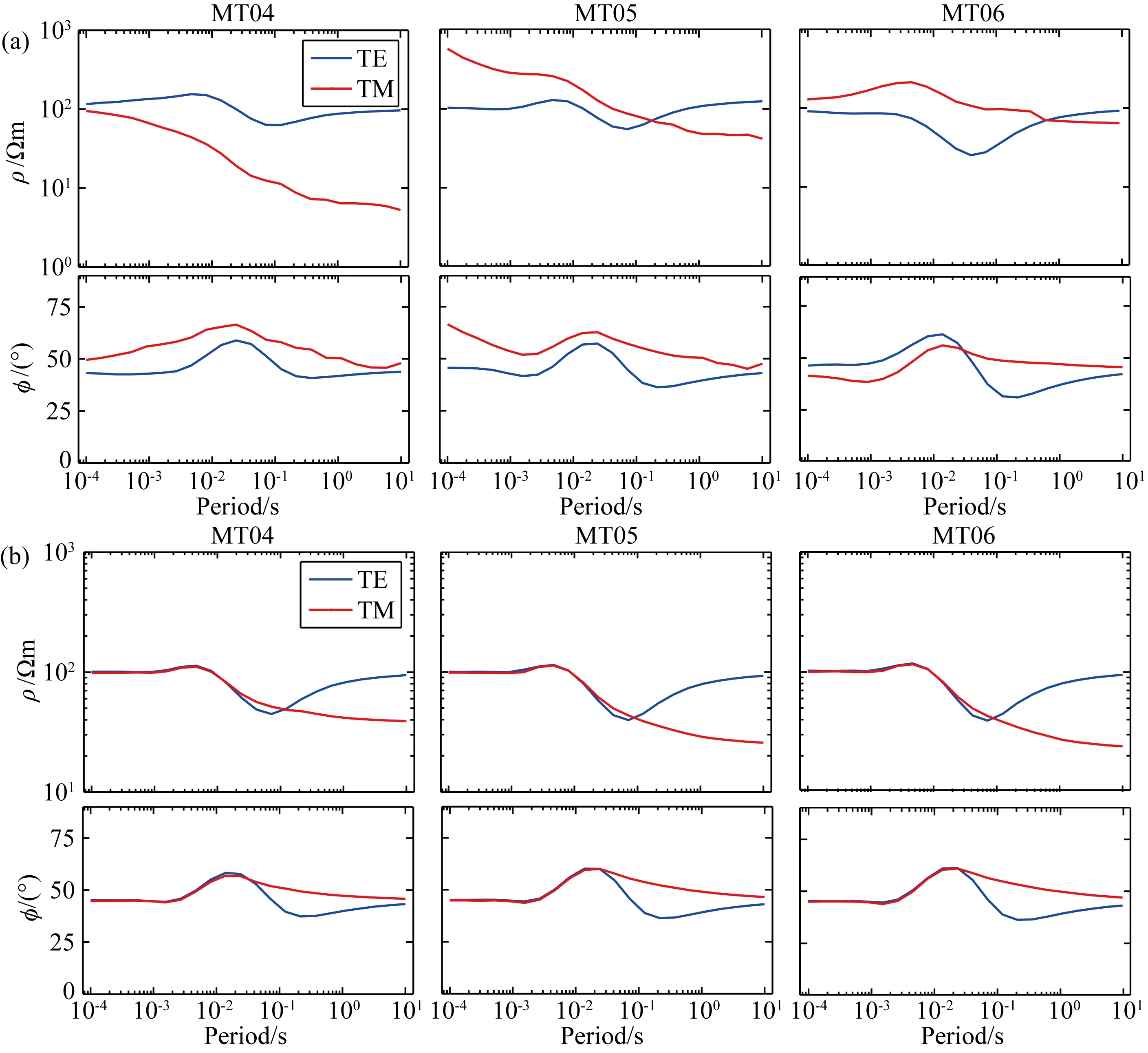
图3 MT04，MT05，MT06测点视电阻率和相位响应

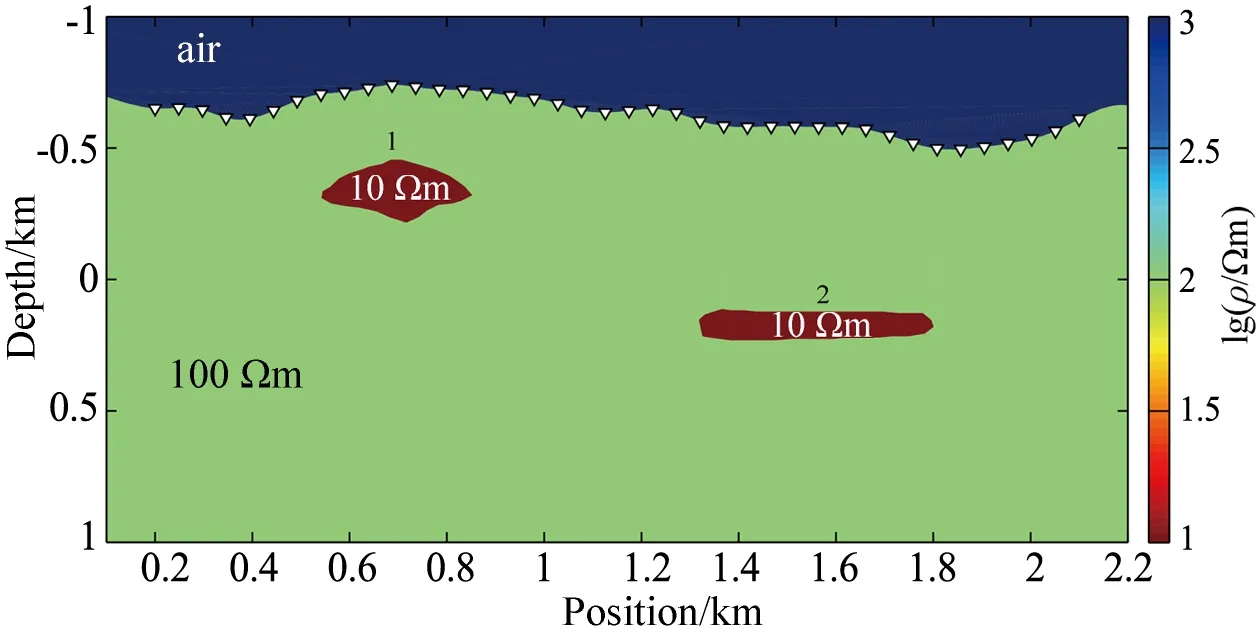
图4 金属矿模型（其中1、2为低阻体编号）

以图4模型进行网格剖分，初始网格划分为2035个三角单元（图5a），对单元误差取对数值显示，其分布如图5b所示.采用四线程对初始网格细化，以其中一个线程为例，该线程负责最后10个测点的自适应正演运算，经过8次细化，生成18854个三角单元（图5c），单元误差达到误差阈值以内（图5d）则停止计算.网格主要在电性分界处即低阻体边界和测点附近进行细化，图5e显示测点附近网格细化信息.其余三个线程同时进行自适应细化过程，共耗时123 s.

利用上述模型的正演数据添加4%的随机噪声进行Occam反演，对于目标区域采用小三角单元细致剖分，周围背景区域则粗糙剖分.反演初始模型如图6，其中包含5958个电阻率为100 Ωm三角单元.

带地形反演结果（图7a）显示1号和2号低阻体中心位置，可圈定出1号低阻体的轮廓，2号低阻体边界较模糊.图7b为相同数据平地反演结果，相对于带地形反演，低阻体出现中心位置偏移及范围扩大的情况，且在近地表处存在虚假异常也称为静态效应.地形是引起静态效应的原因之一，常规处理中，反演前会进行静态效应校正，用以消除浅层假异常现象，常用方法为整体平移数据曲线，这需要丰富的经验且平移结果不一定准确，带地形反演不能完全消除但可以有效地抑制静态效应.

为了验证该算法对浅部薄层低阻矿床的反演效果，我们建立图8a所示的地电模型，模型分为两层，上层电阻率为100 Ωm，层厚约870 m；下层为1000 Ωm，上层存在10 Ωm的低阻体，中心埋深450 m.测点、地形、频点设置与图4模型一致.反演结果（图8b）较好地显示薄层低阻体的中心位置，可识别下层高阻带，且地层分界明显.

在我国地形起伏的山区中，构造发育复杂，常见褶皱、断层分布.建立相应的综合褶皱模型（图9a）进行反演，其中以向斜为主，连接2个小型背斜，10和100 Ωm地层互层分布.测点、地形、频点设置与图4模型一致.反演结果（图9b）显示该褶皱的大致轮廓，地层分层清晰，可看出中部向斜构造.

表1给出了上述三个模型反演耗时，RMS误差及粗糙度.由于本文模型运算采用四线程，模型每更新一次，便重新开始自适应细化，导致反演时间大大增加.在实际应用中，处理大量的数据需要更多的时间，如何优化算法是亟待解决的问题.

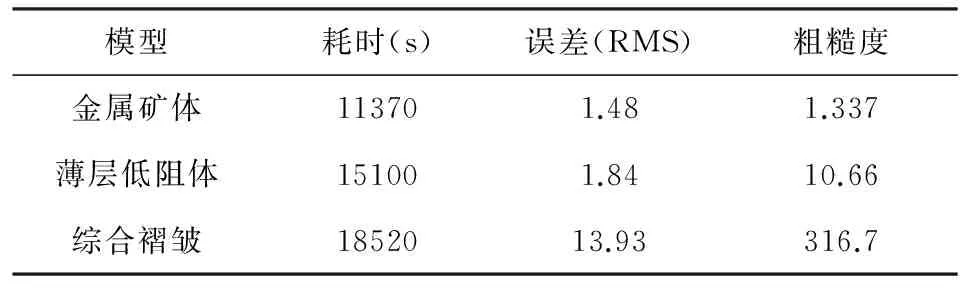
表1 反演耗时、误差及粗糙度列表

4 实测资料解释

工区位于中国西南山地矿区，区内地形起伏剧烈.该区地表水系发育，矿区出露地层比较单一，主要为中三叠统许满组及第四系，但构造发育复杂，主要为褶皱、断裂和节理.数据采集使用加拿大phoenix公司V8多功能电法仪，通过不极化电极测量Ex、Ey两道正交的电场水平分量数据，磁传感器测量Hx、Hy、Hz三道正交的磁场分量数据，从而实现五个电磁场分量的电磁测深数据采集.采集频率范围设置为10400～0.35 Hz，在低频处截屏到1 Hz，探测深度约地下2 km以内电性结构.数据噪声干扰不强，在高频有一天然死频带，采用D+方法进行处理.受地形影响，TM和TE曲线首端较多分离，拟断面图“挂面条”现象严重.

选择工区中A3测线中部进行反演.测线由西南向东北方向布设，最大高差242 m，地形起伏明显.工区布置如图10所示（中间测线为A3），图左下角红色点表示反演起始测点，右上角红色点为终点.A3测线所在位置出露地层为中三叠统许满组第三段（T2xm3），其包含的主要岩矿石电性见表2.图10显示A3测线中部穿越一大型向斜构造和一背斜构造，测线末端发育一系列小型褶皱，与两大褶皱主轴近似平行，测线中部和末端分别穿越小型河流.

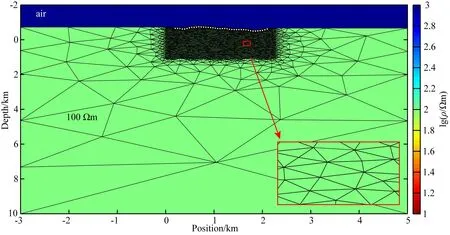
图6 反演初始模型

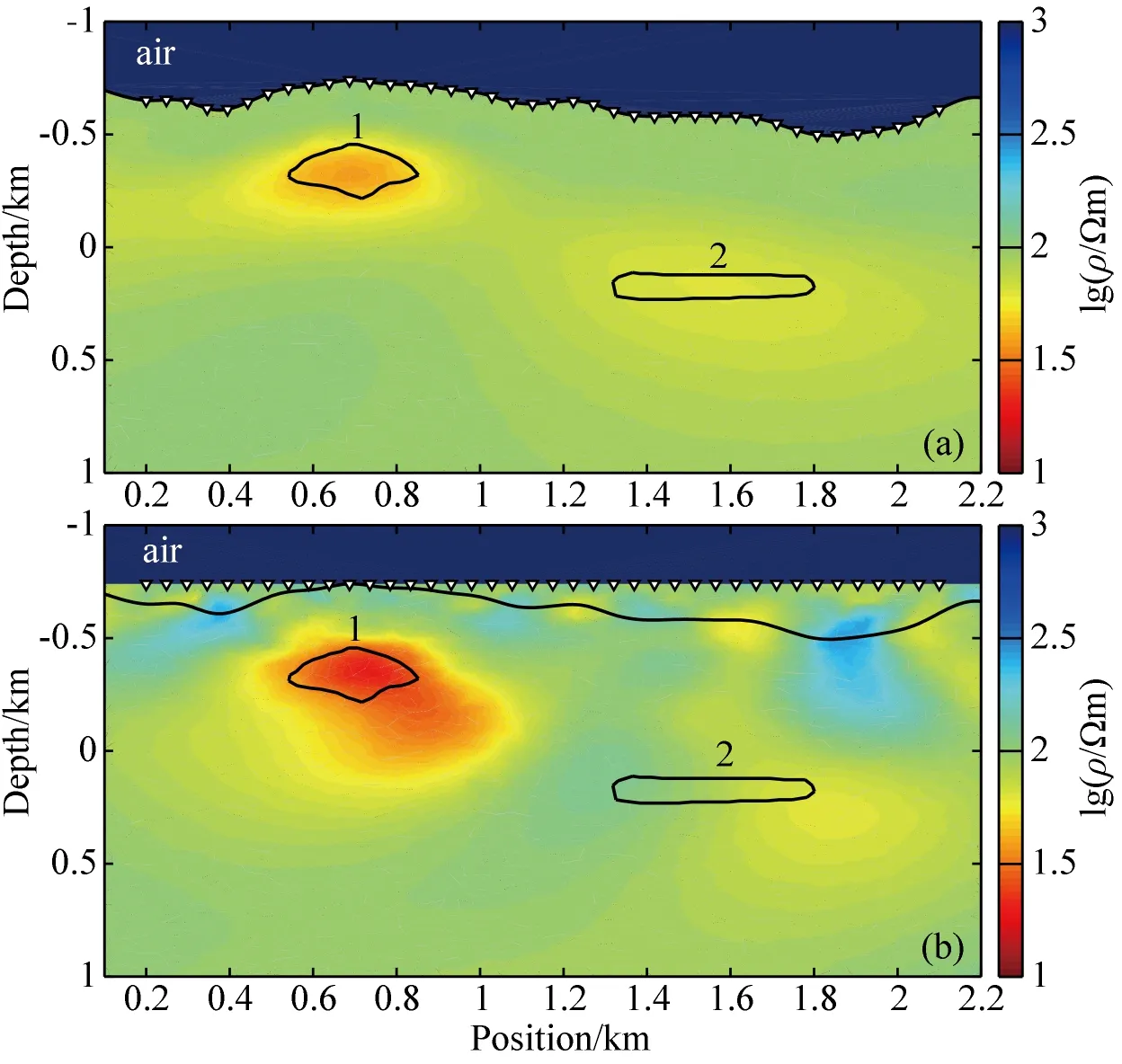
图7 金属矿模型反演结果（其中1、2是低阻体编号）

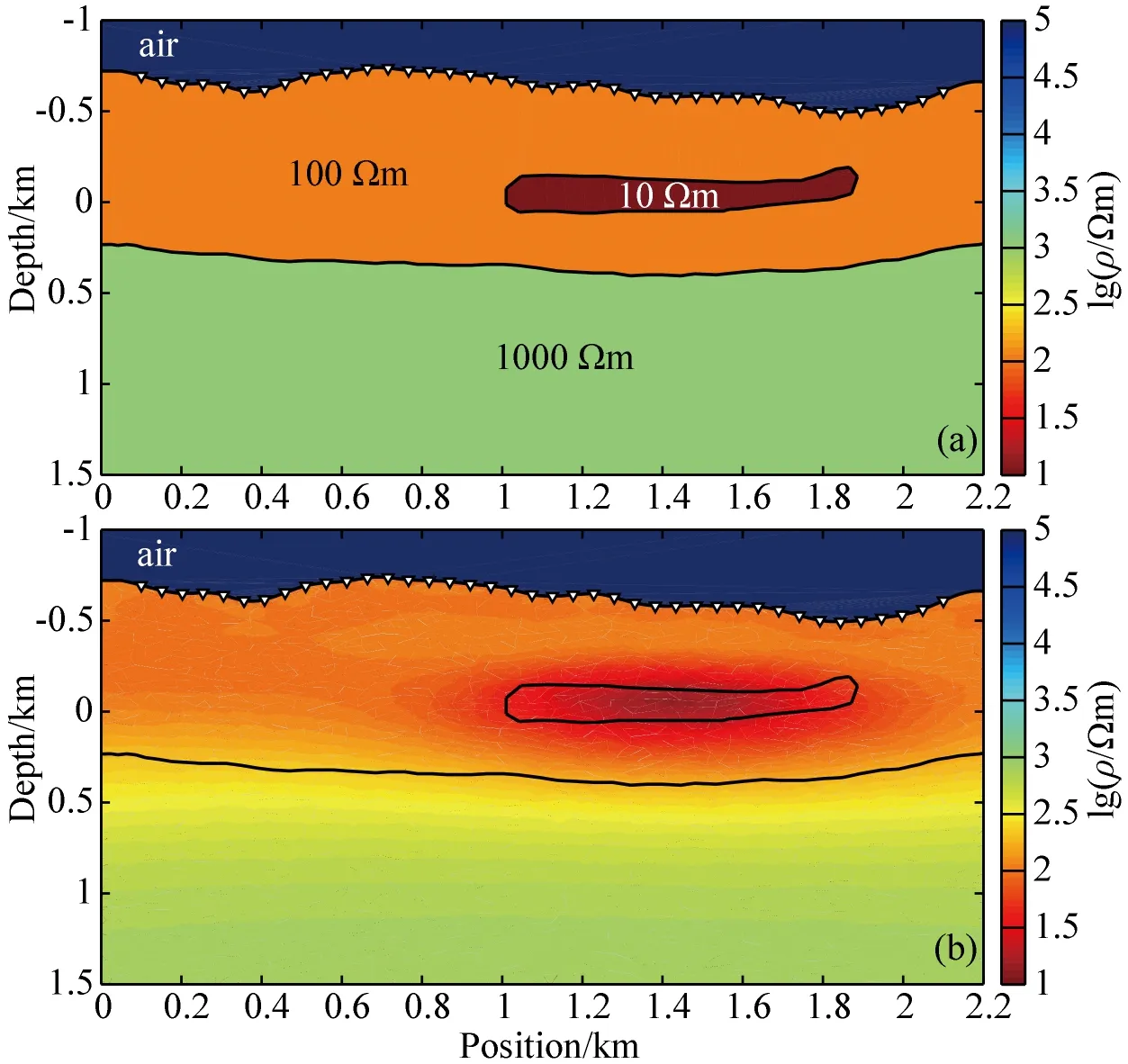
图8 薄层低阻体模型

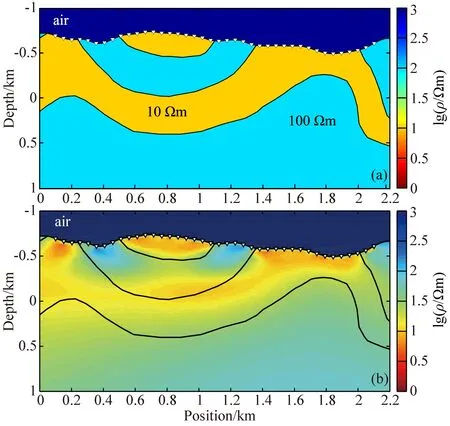
图9 综合褶皱模型

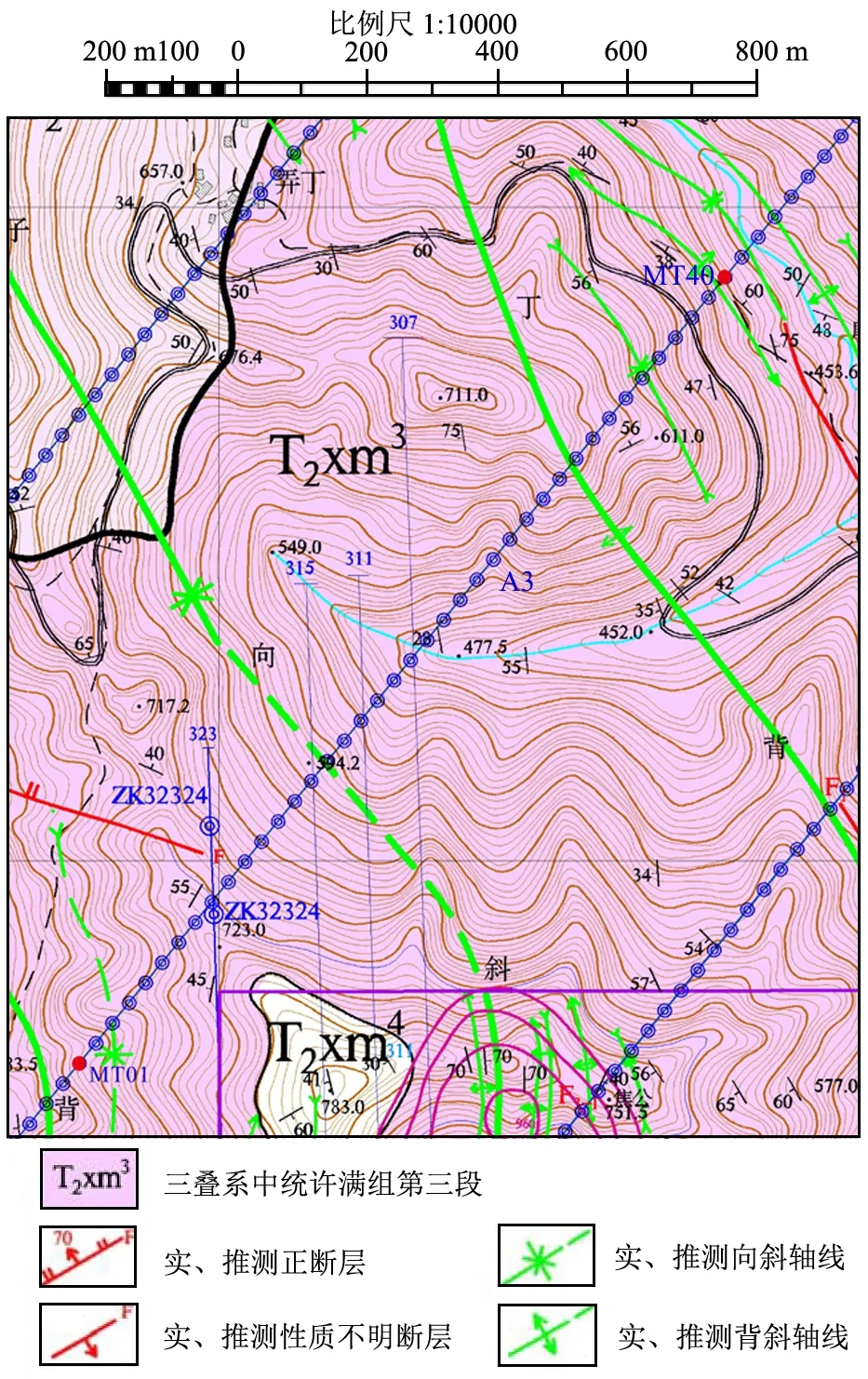
图10 工区地形地质及工程布置图

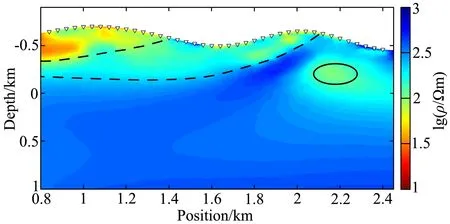
图11 A3测线反演结果

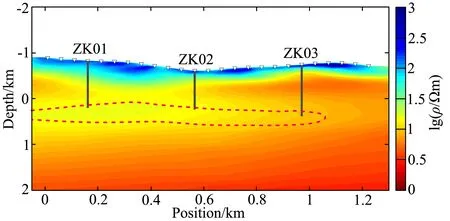
图12 锰矿实测MT数据反演结果

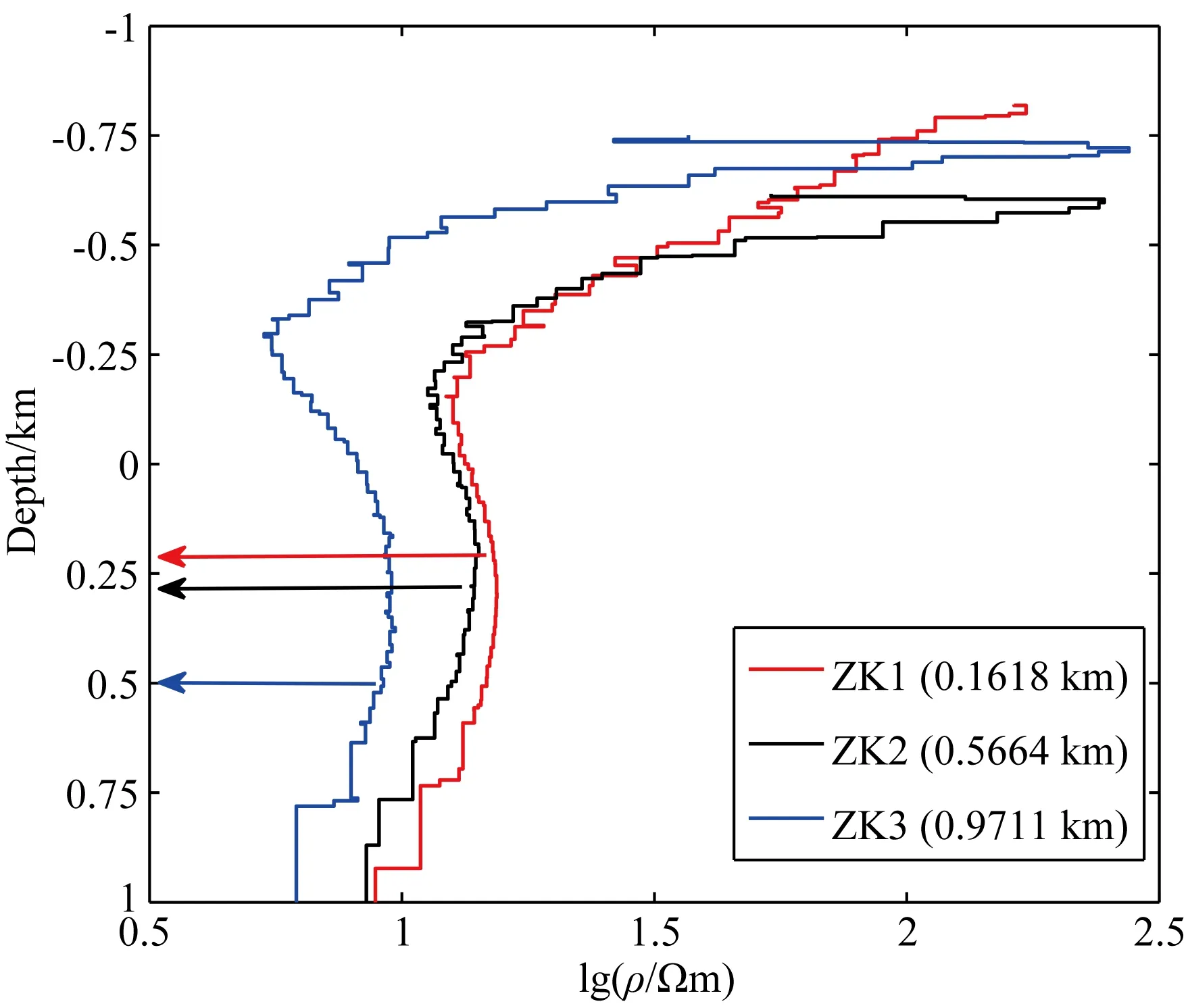
图13 电阻率测深曲线

A3测线中部共40个测点，测点间距约40 m，全长1600 m，频率范围1～10400 Hz，共53个频点，反演共耗时31230 s，RMS为3.74.结果如图11所示，大致可划分为三层电性层，黑色虚线表示地层线，浅地表处为低阻层，随深度增加电阻率逐渐上升，变化范围10～1000 Ωm，与表2所列T2xm3地层电阻率变化情况一致；反演结果显示背斜和向斜构造，背斜上部被剥蚀，整体电性表现为高阻，在其内部包含低阻体.工区地质资料显示该处断层、裂隙、水系发育丰富，推测该低阻体成因可能是地表水沿裂隙渗漏使该处呈现低阻性质.

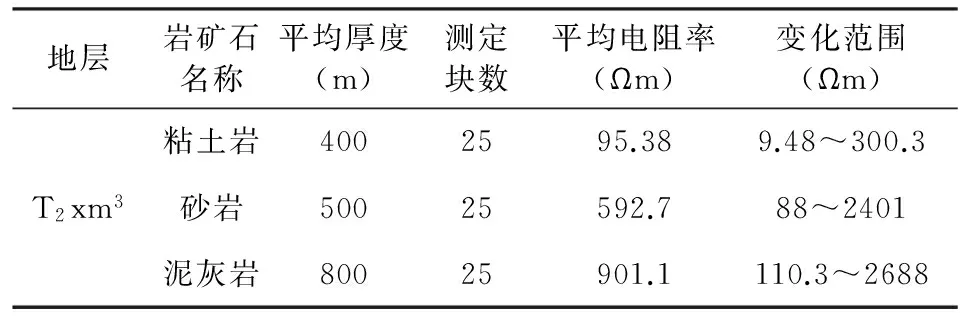
表2 测区主要岩矿石电阻率统计表

另一组数据为寻找锰矿实测电磁数据，锰矿成矿地质体主要由炭质、粉砂质粘土岩夹条带状、块状菱锰矿组成，其综合电性特征表现为低电阻率特征，其上覆地层为含砾砂岩、细晶白云岩等高电阻率岩性.

测线共25个测点，全长1200 m，0.35～10400 Hz共60个频点.其反演结果如图12所示，地层分层明显，浅部地层为高阻，厚度约200～300 m，随深度增加电阻率逐渐减小，在200 m深度处电阻率有增大趋势，之后又逐渐减小.该测线处分布有三口钻孔，如图中黑色圆柱所示，分别位于测线前段（ZK01）、中段（ZK02）和后段（ZK03）.ZK01见矿深度214 m；ZK02见矿深度261 m；ZK03见矿深度501 m.反演结果中钻孔处视电阻率随深度变化曲线如图13，括号内的数字代表钻孔所在水平位置，箭头指向见矿深度.三条测深曲线变化趋势一致，电阻率随深度迅速减小后又缓慢回升，见矿深度并不在视电阻率最小处，而是在视电阻率缓慢回升带，结合反演结果和钻孔资料用红色虚线在图12中圈定出成矿构造带大致范围.

5 结论

本文利用非结构自适应有限元算法研究地形对MT正演数据的影响，该方法能够真实地模拟起伏地形、不规则异常体及复杂形态的地质构造.研究结果表明地形对TE模式影响很小，对TM模式影响远大于TE模式，与平地视电阻率正演曲线相比，TM模式在山峰处低频部分下降，斜坡处曲线整体向上平移，在山谷处高频部分上扬.

将自适应有限元与Occam算法结合进行带地形反演运算，通过理论模型试算和分析，结果证明了该算法能清晰识别出异常体的中心位置且分层性良好，与平地反演结果相比，不会在浅部产生虚假异常，能有效抑制静态效应.应用于电磁实测数据反演结果显示了地层分层信息、背斜构造、见矿层位，探测的地质结构和圈定的成矿构造带均与已有地质资料相符合，表明该算法具有较强的实用性，可用于实测资料解释分析.

在此基础上，将继续研究带地形反演条件下如何正确进行静态校正，优化算法缩短反演计算时间，并根据其他已知信息进行模型约束反演和联合反演，最终将非结构网格引入起伏地形下大地电磁三维正反演研究中.

致谢 感谢中国地质科学院吕庆田研究员和中南大学汤井田教授对文章的悉心指导，对手稿提出的意见丰富了文章的内容.

Chen L S. 1981. Application and improvement of finite element method in forward calculation of geo-electromagnetic field.GeophysicalProspectingforPetrole（in Chinese）, （3）: 84-103.

Coggon J H. 1971. Electromagnetic and electrical modeling by the finite element method.Geophysics, 36（1）: 132-155.

Constable S C, Parker R L, Constable C G. 1987. Occam′s inversion: A practical algorithm for generating smooth models from electromagnetic sounding data.Geophysics, 52（3）: 289-300.

Franke A, Börner R U, Spitzer K. 2007. Adaptive unstructured grid finite element simulation of two-dimensional magnetotelluric fields for arbitrary surface and seafloor topography.GeophysicalJournalInternational, 171（1）: 71-86.

Gao J H, Tong T G, Qiang J K, et al. 2010. A magnetotelluric study of geothermal resources in Kaifeng depression, He′nan Province.GeophysicalandGeochemicalExploration（in Chinese）, 34（4）: 440-443.

Ghaedrahmati R, Moradzadeh A, Fathianpour N, et al. 2014. Investigating 2-D MT inversion codes using real field data.ArabianJournalofGeosciences, 7（6）: 2315-2328.

He M X, Hu X Y, Ye Y X, et al. 2011. 2.5D controlled source audio-frequency magnetotellurics Occam inversion.ProgressinGeophysics（in Chinese）, 26（6）: 2163-2170, doi: 10.3969/j.issn.1004-2903.2011.06.033.

Hu X Y, Peng R H, Wu G J, et al. 2013. Mineral exploration using CSAMT data: Application to Longmen region metallogenic belt, Guangdong Province, China.Geophysics, 78（3）: B111-B119.

Key K, Weiss C. 2006. Adaptive finite-element modeling using unstructured grids: The 2D magnetotelluric example.Geophysics, 71（6）: G291-G299.Key K, Ovall J. 2011. A parallel goal-oriented adaptive finite element method for 2.5-D electromagnetic modelling.GeophysicalJournalInternational, 186（1）: 137-154.

Li R, Tang J, Dong Z Y, et al. 2014. Deep electrical conductivity structure of the southern area in Yunnan Province.ChineseJournalofGeophysics（in Chinese）, 57（4）: 1111-1122, doi: 10.6038/cjg20140409.

Li Y G, Key K. 2007. 2D marine controlled-source electromagnetic modeling: Part 1—An adaptive finite-element algorithm.Geophysics, 72（2）: WA51-WA62.Li Y G, Pek J. 2008. Adaptive finite element modelling of two-dimensional magnetotelluric fields in general anisotropic media.GeophysicalJournalInternational, 175（3）: 942-954.

Liu J X, He H, Liu H F, et al. 2009. 2D inversion of VES data under rolling topography and its application.ComputingTechniquesforGeophysicalandGeochemicalExploration（in Chinese）, 31（4）: 293-296.

Liu X J, Wang J L, Yu P. 2007. Secondary field-based two-dimensional magnetotelluric numerical modeling by finite element method.JournalofTongjiUniversity（NaturalScience） （in Chinese）, 35（8）: 1113-1117.

Liu Y, Lü Q T, Meng G X, et al. 2012. Joint electromagnetic and seismic inversion survey: status and prospect.ProgressinGeophysics（in Chinese）, 27（6）: 2444-2451, doi: 10.6038/j.issn.1004-2903.2012.06.019.

Lu G F, Wu X G. 2014. Application of comprehensive electrical prospecting method in the exploration of the concealed metallic deposit.MineralExploration（in Chinese）, 5（4）: 617-622.

Lü Q T, Shi D N, Tang J T, et al. 2011. Probing on deep structure of middle and lower reaches of the Yangtze metallogenic belt and typical ore concentration area: A review of annual progress of SinoProbe-03.ActaGeoscienticaSinica（in Chinese）, 32（3）: 257-268.

Ovall J S. 2006. Asymptotically exact functional error estimators based on superconvergent gradient recovery.NumerischeMathematik, 102（3）: 543-558.

Rodi W L. 1976. A technique for improving the accuracy of finite element solutions for magnetotelluric data.GeophysicalJournalInternational, 44（2）: 483-506.

Shewchuk J R. 2002. Delaunay refinement algorithms for triangular mesh generation.ComputationalGeometry, 22（1-3）: 21-74.

Siripunvaraporn W, Sarakorn W. 2011. An efficient data space conjugate gradient Occam′s method for three-dimensional magnetotelluric inversion.GeophysicalJournalInternational, 186（2）: 567-579.

Sudha, Tezkan B, Siemon B. 2014. Appraisal of a new 1D weighted joint inversion of ground based and helicopter-borne electromagnetic data.GeophysicalProspecting, 62（3）: 597-614.

Tong X Z, Liu J X, Guo R W. 2009. Solution strategies for complex 2D/3D magnetotelluric forward modeling based on the finite element method.ComputerizedTomographyTheoryandApplications（in Chinese）, 18（1）: 47-54.

Wang X B, Li Y N, Gao Y C. 1999. Two dimensional topographic responses in magneto-telluric sounding and its correction methods.ComputingTechniquesforGeophysicalandGeochemicalExploration（in Chinese）, 21（4）: 327-332.

Wannamaker P E, Stodt J A, Rijo L. 1987. A stable finite element solution for two-dimensional magnetotelluric modelling.GeophysicalJournalInternational, 88（1）: 277-296.

Wu G J, Hu X Y, Huo G P, et al. 2012. Geophysical exploration for geothermal resources: An application of MT and CSAMT in Jiangxia, Wuhan, China.JournalofEarthScience, 23（5）: 757-767.

Xia X Y, Wang J X, Liu J C, et al. 2012. The application of magnetotelluric sounding to lithofacies division in oil and gas exploration of northern nanpangjiang area.GeophysicalandGeochemicalExploration（in Chinese）, 36（2）: 174-179.

Zhan Y, Zhao G Z, Wang L F, et al. 2014. Deep electric structure beneath the intersection area of West Qinling orogenic zone with North-South Seismic tectonic zone in China.ChineseJ.Geophys. （in Chinese）, 57（8）: 2594-2607, doi: 10.6038/cjg20140819.

Zhang J D, Yang X Y, Liu C Z, et al. 2012. The fine deep structure of the northern margin of the Dabie Orogenic Belt from gravity-magnetic-electrical-seismic combination survey.ChineseJ.Geophys. （in Chinese）, 55（7）: 2292-2306.

Zhang K, Wei W B, Ye G F. 2008. The actualization of 2D finite-element magnetotelluric forwarding on Matlab.SeismologicalandGeomagneticObservationandResearch（in Chinese）, 29（5）: 83-88.

Zhang X, Hu W B, Yan L J, et al. 1999. Effects and correction of topography in magnetotelluric sounding.JournalofJianghanPetroleumInstitute（in Chinese）, 21（1）: 37-41.

Zhao G M, Li T L, Wang D Y, et al. 2008. Secondary field-based two-dimensional topographic numerical simulation in magnetotellurics by finite element method.JournalofJilinUniversity（EarthScienceEdition） （in Chinese）, 38（6）: 1055-1059.

Zhao H, Liu Y, Li Y G. 2014. Adaptive finite element forward modeling for two-dimensional marine magnetotelluric fields.OilGeophysicalProspecting（in Chinese）, 49（3）: 578-585.

Zyserman F I, Guarracino L, Santos J E. 1999. A hybridized mixed finite element domain decomposed method for two dimensional magnetotelluric modelling.Earth,PlanetsandSpace, 51（4）: 297-306.

附中文参考文献

陈乐寿. 1981. 有限元法在大地电磁场正演计算中的应用及改进. 石油物探, （3）: 84-103.

高景宏, 佟铁钢, 强建科等. 2010. 开封凹陷区地热资源大地电磁测深研究. 物探与化探, 34（4）: 440-443.

何梅兴, 胡祥云, 叶益信等. 2011. 2.5维可控源音频大地电磁法Occam反演理论及应用. 地球物理学进展, 26（6）: 2163-2170, doi: 10.3969/j.issn.1004-2903.2011.06.033.

李冉, 汤吉, 董泽义等. 2014. 云南南部地区深部电性结构特征研究. 地球物理学报, 57（4）: 1111-1122, doi: 10.6038/cjg20140409. 柳建新, 何欢, 刘海飞等. 2009. 起伏地形垂直电测深二维反演及应用. 物探化探计算技术, 31（4）: 293-296.

刘小军, 王家林, 于鹏. 2007. 基于二次场的二维大地电磁有限元法数值模拟. 同济大学学报（自然科学版）, 35（8）: 1113-1117.

刘彦, 吕庆田, 孟贵祥等. 2012. 大地电磁与地震联合反演研究现状与展望. 地球物理学进展, 27（6）: 2444-2451, doi: 10.6038/j.issn.1004-2903.2012.06.019.

陆桂福, 吴新刚. 2014. 综合电法勘查在隐伏金属矿勘查中的应用效果. 矿产勘查, 5（4）: 617-622.

吕庆田, 史大年, 汤井田等. 2011. 长江中下游成矿带及典型矿集区深部结构探测——SinoProbe-03年度进展综述. 地球学报, 32（3）: 257-268.

童孝忠, 柳建新, 郭荣文. 2009. 复杂二维/三维大地电磁的有限单元法正演模拟策略. CT理论与应用研究, 18（1）: 47-54.

王绪本, 李永年, 高永才. 1999. 大地电磁测深二维地形影响及其校正方法研究. 物探化探计算技术, 21（4）: 327-332.

夏训银, 王建新, 刘俊昌等. 2012. 大地电磁测深在南盘江北部地区油气勘探中的应用. 物探与化探, 36（2）: 174-179.

詹艳, 赵国泽, 王立凤等. 2014. 西秦岭与南北地震构造带交汇区深部电性结构特征. 地球物理学报, 57（8）: 2594-2607, doi: 10.6038/cjg20140819.

张交东, 杨晓勇, 刘成斋等. 2012. 大别山北缘深部结构的高精度重磁电震解析. 地球物理学报, 55（7）: 2292-2306.

张昆, 魏文博, 叶高峰. 2008. 二维有限元大地电磁正演模拟在Matlab上的实现. 地震地磁观测与研究, 29（5）: 83-88.

张翔, 胡文宝, 严良俊等. 1999. 大地电磁测深中的地形影响与校正. 江汉石油学院学报, 21（1）: 37-41.

赵广茂, 李桐林, 王大勇等. 2008. 基于二次场二维起伏地形MT有限元数值模拟. 吉林大学学报（地球科学版）, 38（6）: 1055-1059. 赵慧, 刘颖, 李予国. 2014. 自适应有限元海洋大地电磁场二维正演模拟. 石油地球物理勘探, 49（3）: 578-585.

（本文编辑 何燕）

A study of two-dimensional MT inversion with steep topography using the adaptive unstructured finite element method

HAN Qi1, HU Xiang-Yun1*, CHENG Zheng-Pu1, YANG Bing-Nan2, CAI Jian-Chao1, WEI Wei1

1HubeiSubsurfaceMulti-scaleImagingKeyLaboratory,InstituteofGeophysicsandGeomatics,ChinaUniversityofGeosciences,Wuhan430074,China2GuizhouGeologyandMineralsBureau，GuizhouTongren554300,China

The structured grid has its limit when simulating complicated topography, especially applying the MT method in mountainous areas where the effect of terrain cannot be ignored. Unstructured triangular grids permit efficient discretization of complex modelling domains such as those containing topography, dipping strata and multiple scale structures. To ensure the accurate result of forward modeling, we refine grids according element errors during gridding the model. We combine the adaptive finite element and the Occam method, and develop a parallel processing scheme that can efficiently improve the computational speed of forward modeling and inversion. By comparing two synthetic models, first we discuss the terrain effect by building two different models. Then forward modeling and inversion are conducted on a series of models with steep topography. The application of this approach to processing of real data from Southwest China shows that the adaptive unstructured finite element method is a powerful tool to analyze MT data of complex features such as steep surface topography.

Magnetotelluric; Adaptive finite element; Topography; Inversion

国家科技专项“深部矿产资源立体探测技术与试验”（SinoProbe-03）、国家自然科学基金项目（41274077，41474055）、中国地质调查局项目（12120113101800）联合资助.

韩骑，女，1990年生，硕士研究生，主要从事大地电磁二维起伏地形正反演研究.E-mail:hanqi426@gmail.com

*通讯作者 胡祥云，男，1966年生，教授，主要从事电法勘探理论及应用研究.E-mail:xyhu@cug.edu.cn

10.6038/cjg20151228.

10.6038/cjg20151228

P631

2015-05-28，2015-11-12收修定稿

韩骑， 胡祥云， 程正璞等. 2015. 自适应非结构有限元MT二维起伏地形正反演研究.地球物理学报，58（12）:4675-4684,

Han Q, Hu X Y, Cheng Z P, et al. 2015. A study of two-dimensional MT inversion with steep topography using the adaptive unstructured finite element method.ChineseJ.Geophys. （in Chinese）,58（12）:4675-4684,doi:10.6038/cjg20151228.