链条下落运动问题浅析

于同旭，张文彬，许 腾，曹则贤

中国科学院物理研究所，北京 100190

链条下落运动问题浅析

于同旭†，张文彬，许 腾，曹则贤

中国科学院物理研究所，北京 100190

链条的力学问题在物理学的发展过程中一直备受人们的关注，并与重大的工程实践有着密切联系。下落链条作为典型的变质量体系，经常被引为力学教科书上的范例。然而，对于链条下落运动的认识依然存在着诸多分歧有待澄清。链条的下落运动行为依赖于其初始构型，本文选取4种设定情形进行介绍，并简要分析不同运动行为的特征。

下落链条；变质量体系；加速度；堆积构型；几何轮廓

对物理学的发展稍有了解的人会注意到这样一个事实：对于下落问题的思索似乎是一直贯穿着该学科从古到今的发展。试举几例：据传伽利略(1564—1642)由在比萨斜塔做的两个不同质量的同种物体同步下落的演示实验而推翻了在中世纪自然哲学中占统治地位的亚里士多德(公元前384—公元前322)的观点——同一高度同时释放的两个物体重物先落至地面[1]；牛顿(1642—1727)由苹果落地的联想，得出天体的运动与地面附近物体的下落运动同为有心力所导致的结论，从而发现了万有引力定律[2]；(需要说明的是，这两则传闻并没有翔实可靠的历史记录，更可能的事实是两人在头脑中开展了相应的类似的思想实验(Gedankenexperiment)，通过归谬和演绎得到了上述的结果。)而爱因斯坦(1879—1955)则通过构建自由下落的升降机的思想实验，得出了广义相对论的等效性原理，即一个相对于惯性系做匀加速运动的非惯性系与存在引力场等效[3]。从上面这3个广为人知的例子可见，对于下落运动问题的每一步深刻认识都带来了物理学的重要发展。

在上述3例思想实验中，为了抽离出现象背后的基本物理原理，忽略下落物的本征属性是必要的。不过当基本原理的框架建立以后，一个学科(尤其物理学)的发展总是朝着认识具体的事物和现象而行，此时体系内禀的特征将必须纳入考虑。对于下落的连续体(可作刚性近似)，当其处于地面附近(不计重力变化)，速率较小(不计阻力影响)时，其运动形式为竖直向下的匀加速运动(加速度为g)。这里要求的刚性近似、接近地面、较小速率即构成体系作自由落体运动的必要前提条件。本文旨在探讨链条这一体系的下落运动所具有的一些有别于自由落体运动的特征。

链条、绳索、鞭子这些准一维柔性物体的静力学和动力学行为研究在物理学中也有着悠久的历史，并与一些显赫的名字相关。据记载，最早依然是由伽利略指出两端固定的松弛的链条的轮廓近似为抛物线状[4]。当然这一结论并不准确，后来是由Christiaan Huygens (1629—1695)、Gottfried Leibniz (1646—1716)、John Bernoulli (1667—1748)独立地发现其轮廓应为悬链线(catenary)[5]，由其间的张力来承受链条的重量；而在1675年Robert Hooke (1635—1703)发现由压应力来承重的薄拱坝(thin arch)，其拱形应为倒悬线状(inverted catenary)[6]。此后建筑师便将反垂曲线形拱(catenary arch)融入到建筑设计中，他们当中最为典型的当属西班牙建筑师Antoni Gaudí (1852—1926)，他不但将这一拱形大量地用到建筑作品中，还利用悬线来构建倒置的建筑模型。图1(a)、1(b)展示的分别是Gaudí的建筑杰作Casa Milà中包含的反垂曲线形拱元素和在设计Colònia Güell时用到的悬线模型[7]。

图1 Antoni Gaudí建筑设计中的反垂曲线形拱元素：(a) Gaudí的建筑杰作Casa Milà中包含的反垂曲线形拱元素；(b)在设计Colònia Güell时用到的悬线模型

链条(绳索)的力学行为除对建筑(美)学的发展造成影响之外，还与19世纪下半叶一项举世瞩目的重大工程项目密切相关，那就是大西洋海底电缆的铺设(热力学的奠基人之一著名的Lord Kelvin (1824—1907)即参与其中，并因这项工程贡献而被授予勋爵爵位[8])。首次铺设海底电缆的努力以失败告终，这促使当时人们对于其所涉及的动力学问题进行研究。Sir George Biddell Airy (1801—1892)在1858年指出，被以恒定速率牵引的绳索其稳定形状同样为悬链线形，从静止平衡状态向稳定运动的过渡其效果只是造成绳索的张力中包含正比于速度平方的一项[9](这一速度平方项将会出现在后面各部分的讨论中)。

通过上述的历史回顾大家可能形成这样一种印象，即链条(绳索)的力学问题业已得到了详尽的研究，不大可能孕育新的研究亮点。但事实并非如此。想必大家对于神舟七号宇航员出舱的画面还记忆犹新，一定留意到了连接飞船和宇航员的缆索，它是宇航员太空行走的生命维系。存在梯度变化的空间引力场环境以及飞船这一非惯性系给缆索的运动描述带来了新的复杂性，这构成了绳索动力学研究中的一个重要方向[10]。另举一例，长久以来多重因素一直制约着中国自建航母的发展，其中一个主要的技术障碍即为航母阻拦索的设计。阻拦索用于将舰载机高速拦停，是舰载机名副其实的“生命线”，如何在大冲力条件下保证其安全可靠且具有较长的使用寿命一直是研究的焦点[11]。

本文不打算讨论链条所涉及的这诸多工程力学问题，而是撷取几个方面考察链条下落运动这一物理过程。我们将会看到，即便是链条下落运动这样习以为常的现象，也会表现出许多意料之外的行为特征，从而考验直观的物理思维。首先需要提请注意这样一个特点：宏观物体的力学描述通常采取连续性假设，这便于给出相对简单的数学解析表达(通常为微分形式)，但是对于复杂的力学体系，解析求解即使不是不可能的，在时效上也是不经济的。不过计算技术的发展提供了实现高效求解的可能。我们知道，计算机数值方法要求对体系进行离散化处理，需要将连续体进行单元剖分，把描述连续体的微分方程写成差分方程组的形式，从而利用有限元或差分方法等离散化的数学工具来进行近似求解。然而链条本身是由多个链节联结而成，其自身已构成离散体的集合，因此可以直接用差分方程来给出链条运动的精确描述。对于绳索和鞭子，宏观来看它们本身即为连续体，其运动方程可能存在着精确的微分形式，但是当进行数值求解时，实际上还是将两者近似看作由多个小段相互连接构成，这一点类似于链条，利用处理链条的计算方法即可对其运动方程进行求解。当然数学处理方法上的等效性，是基于链条、绳索具有相似的力学行为。我们知道，物体对外界的不同激励产生的特征力学响应是反映物体状态的一个重要指标，例如抗剪切性质的有无可以作为区分固液体状态的标志。链条、绳索这些准一维柔性体在其长度方向上可以承受一定的张应力，而无法承受压应力，它们表现出来的一些动力学行为，往往与其间的张应力有关。考虑到这些相似性，并由于篇幅的限制，本文只对链条的下落运动问题进行描述，相当一部分结果同样地适用于绳索的情形。

另外需要注意的一点是，虽然运动本身的存在已决定了描述其行为的方程解的存在性，但是要限制解的唯一性，则取决于体系设定的初始条件和边界条件。本文选取了下落链条的4种构型，我们将会看到，对于这些不同的设定条件，链条的运动都表现出了形式上的差异。

1 一端固定，一端释放之链条的下落运动

前已提到，两端固定的松弛链条的平滑轮廓(也即不考虑链节的固有长度和刚性)为悬链线，当固定点很靠近时，我们将这一轮廓称为窄悬链线(narrow catenary)，如图2(a)所示。当链条一端解除固定时，大家可能直观地认为该自由端将在重力作用下以加速度 g下落，许多教科书上也是给出这样的解答。然而事实并非如此，M. G. Calkin和R. H. March[12]首先指出这一错误观点，他们发现自由端落至最低点所经历的时间小于自由下落所需时间，这说明链条下落端的加速度大于重力加速度，下落链段除了受到重力之外链节之间还存在着张力作用。这一结果也为M. Schagerl等[13]所证实，他们发现初始位于同一高度的链端和小钢环在自由下落过程中，钢环逐渐落后于链端，这一实验直接证明了链条下落的加速度大于重力加速度 g。

基于链条的离散特性，我们可以对其下落运动进行解析描述。设定链条一端的固定点为坐标原点和势能零点，选择链节轴向与竖直方向的夹角θi为广义坐标，如此就可以建立每个链节质心的直角坐标(χi, yi)：

从而写出其动能Ti、势能Vi以及整个体系的拉格朗日量L：

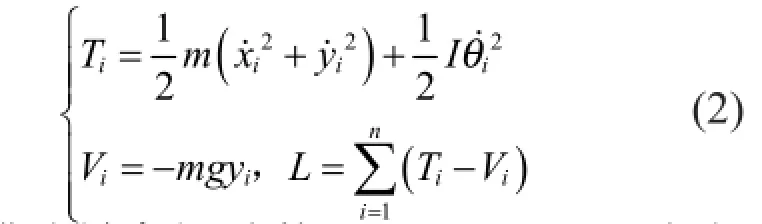
进而写出描述链条运动的Euler-Lagrange方程组：

然而，即便能够写出描述链条运动的微分方程，要实现其解析求解依然十分困难，因此就需要借助于计算机数值模拟。结果表明[13-14]数值模拟确实能与实验结果进行很好的比较。

另外存在这样一种情况，即初始两固定点间距约为单个链节长度，此时可近似认为链条的左右两段平行沿竖直方向悬垂，如图2(b)。对于折叠链条(folded chain)这一情形[15]，在假定下落过程机械能守恒(系统重力势能的变化完全转变为下落链段的动能，而不考虑其他形式的转化)的前提下，体系是可以利用连续性描述进行解析求解的。考虑当链条右端释放时，其重力势能将向动能转化，与此同时，右端链条底部的链节往左端补充，右端链节逐渐减少，这是典型的变质量问题(variable-mass problem)。一般我们将牛顿第二定律写作F=Mv.，不过这是针对质量不变的体系，而更普适的写法应为

其可以用于描述质量变化体系的运动。当系统的外力只是由重力来提供(即F=Mg)时，由上述公式可以知道，质量变化部分的加速度将有别于重力加速度g。对于在此讨论的单端释放链条来说，其运动端质量减小，这意味着M.<0，由此明显知其下落的加速度将大于重力加速度g。

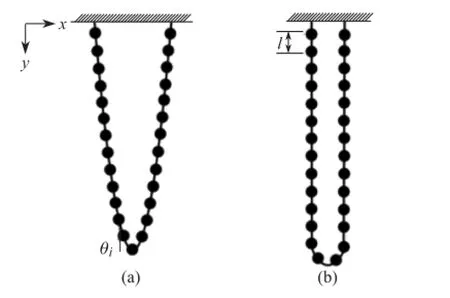
图2 两端固定的悬垂链条：(a) 窄悬链线形；(b) U形折叠

当然针对折叠链条的这一讨论是较为粗糙的，它忽略了单个链节的运动细节以及链条两端的质量交换过程，假定在下落过程中系统重力势能的变化全部转化为运动端的竖直平动动能这一点也值得商榷。由于承载动能部分的链节数目在不断减小，因此其速度不断增加，当最后一个链节补充到左端底部时，链条右端的质量减为零，则其速度将为无穷大。但是这是不符合物理真实的，原因在于：首先我们忽视了一点，即链条两端的质量交换是以单个链节的质量m为单元的，在底部的链节从右端向左端补充时，相应的链节还伴随着以左端底部末端节点为轴的转动，这一转动在链中产生了额外的张力才使得右端链条的加速度大于重力加速度g；其次这一转动过程的能量是由链节原先竖直方向的平动动能转化而来，也即由重力势能转化而来，这说明只考虑链段整体的竖直运动的话，机械能存在一定的耗散。在右端链节向左端底部补充的转动过程中，根据动量定理，临近链节也将发生横向的摆动，摆动会沿链条轴向传播，甚至造成左右两端链条的碰撞，数值模拟已证实了这一点[13-14]。链条中的这一横向波动过程造成了链条竖直下落过程中的机械能损失。另外，由于链条的不可延展性，链条的横向摆动也会造成链条纵向的联动伸缩，如此复杂的运动势必使得简单的连续性描述捉襟见肘。

2 平面堆积之链条的下落运动

上一部分讨论了下落链段的质量逐渐减小的变质量问题，得出其链端的加速度大于重力加速度g的结论。由此可以联想到这样的链条体系，其下落部分的质量逐渐增加，那么链条运动的加速度可能将小于重力加速度g。初始堆积在一个平面上，其一端悬垂于平面边缘竖直下落(不计摩擦)的链条(图3)即符合这一情形。这一问题由来已久，可以回溯到19世纪中叶，并与著名的剑桥大学数学Tripos考试(Tripos一词源于拉丁语，意指三脚凳，过去剑桥大学的本科生要坐在这种凳子上通过各种考试才能获准毕业，赢得该考试头名的学生被称为Senior Wrangler)有莫大渊源。早在1857年Arthur Cayley (1821—1895)就给出了该问题的一个解答[16]，他认为链条在下落过程中机械能不守恒，得出其运动的加速度为g。不过Wong等在文章[17]中提到，在Routh的专著《A Treatise on Dynamics of a Particle》中有这样一条脚注，言及此类变质量问题早在1850年就出现在剑桥有名的私人教师、被誉为Senior-Wrangler Maker的William Hopkins (1793—1866)的训练中；脚注还提到这一问题的一个解答也出现在了由Tait和Steele撰写、出版于1856年的一本关于动力学的著作《A Treatise on Dynamics of a Particle》中。(Cayley、Tait和Routh都曾接受过Hopkins的指导并且分别于1842、1852、1854年赢得了Senior Wrangler称号。)由此这一初始堆积于平面的链条下落问题应称之为Hopkins-Tait-Steele-Cayley(HTSC)问题。Wong还指出，HTSC问题的能量非守恒解在其后一些参加过Tripos考试的人——J. Wolstenholme，H. Lamb，J. M. Jeans——的著作当中也均有出现。

图3 堆积于平面上的链条下落示意图

下面从两个角度来讨论该问题。其一，假定链条在下落过程中只受到重力这一外力作用，那么根据动量定理：=ρgχ（其中ρ为单位长度的链条质量），以及初始条件χ0=0, n0=0，很容易得到n2=gχ，并由n2=2aχ可得链条下落的加速度为a=g。这与Cayley给出的能量非守恒解相一致。另一方面，如果假设链条下落过程机械能守恒，即ρχn2= ρgχ，则将很容易得到·n2=gχ, a=。这样第一种方法将给出ρgχ2的能量损失，它是由平面上静止链条受到下落链条的牵引而造成的。在Arnold Sommerfeld(1868—1951)的《Mechanics》[18]中，其将该能量损失项的引入归于Lazare Carnot(1753—1823)(其子可能更为人所熟知——提出了热力学中著名的卡诺循环的Sadi Carnot(1796—1832)。Lazare Carnot除了是一位工程师和数学家以外，还是法国革命时期拿破仑(1769—1821)的忠实将领之一，其名字被镌刻在埃菲尔铁塔之上)。

上述两种假定给出了不同的运动加速度，那么究竟哪一种描述更贴近物理真实呢？我们知道，下落链条在运动过程中，会带动原本在台面上处于静止的链条，也即会给静止链条一个冲量，使得其以下落链条的速度开始运动，这部分链段构成了运动链条的质量变化项m.=ρn。要施加这一冲量，链条中必须有张力T存在，因此在运用动量定理时只考虑重力的作用是不确切的，= ρgχ+T准确的写法应为(规定向下的方向为正，则T<0)。进而若依Wong的能量守恒的思路，可以利用Euler-Lagrange方程求出T的表达式：以平面边沿为参考点，下落链条的拉格朗日量写为L=ρχn2+ρgχ·，根据Euler-Lagrange得到对比可知T=ρn2，其方向朝下。这与我们的直觉即T<0是相矛盾的：若张力朝下，则链条下落的加速度势必大于重力加速度g。并且Anoop Grewal小组也指出[19]，Wong在论证链条下落过程中机械能守恒这一点时存在着循环论证：假定Euler-Lagrange方程可用已然默认了能量守恒。由此可见上述两种思路似乎都未给出确切的结果。

3 落于平面之链条的下落运动

链条下落端与某一平面接触并在其上堆积是一种常见的现象，这一部分将对此进行讨论。我们会看到，这一下落运动也表现出与自由落体运动不同的特征。考虑竖直链条自由伸展而其底端刚好与平面接触，那么在链条下落过程中其底部链节将逐渐在平面上堆积，平面给予接触链节以冲量使其速度减为零。如果在dt时间内链节的速度由v变为0，则这一过程中动量的变化为dp=-ρvdt·v，根据动量定理，台面施于链节使其静止的力为 f==ρv2。与此同时平台上部的链条其链节数减少，相应地质量减小，这一变质量问题预示着链条下落的加速度将大于重力加速度g。实验结果也显示，链条和与其顶端平齐的小球在同时释放后，顶端链节高度始终低于自由下落的小球的高度(图4)。这是由于链节具有一定的长度以及刚性，链条在台面的堆积并非是集中于一点和仅仅为平动，这一过程中还伴随着链节的转动，转动在链条中产生的张力以及链条自身的重力使得链条下落的加速度大于重力加速度g。

图4 同时下落的链条与小球[20](初始状态，链条顶端与小球平齐；其后，顶端链节的高度低于小球的高度)

可以使链条落于称重装置来定量地考察其与台面之间的相互作用[20]，当链条下落χ高度时，其施于称重台面的力将为已堆积链条的重力ρgχ与-f 的合力，即F= ρgχ+ρv2。如果基于链条自由下落的假定，则v2=2gχ，F=3ρgχ，即理论上称重装置的瞬时读数将是堆积于其上的链段重量的三倍。又由χ=gt2，这一读数将随时间呈抛物线型增加，当链条全部堆积于装置上时，读数显示为整个链条重量的三倍并很快降为链条的重量本身。但实验已经证实链条下落的加速度大于重力加速度g，因此，链条施于台面的力将大于三倍的已堆积链条的重量。不过这是基于连续性假设，而实际上由于链节的离散特性，以及落于台面上的链节由台面提供冲量使其速度减为零需要一定的时间(即便时间很短)，在这一时间段内装置读数会有跳动，构成了测量的噪声。经过平滑滤波可以消除实验噪声，结果显示链条全部落于测量台面的瞬时读数确实大于三倍的链条重量，其后减为链条的重量，并且时间记录显示链条下落所经历的时间确实要短于自由下落所需要的时间。

4 高度差固定之链条的下落运动

进而考察在具有固定高度差(其小于链条总长度)的台面之间的链条的下落运动。由于前面两部分已做了讨论，在此暂先不考虑下落链条初始尚未与下台面接触和最终脱离上台面的情形。在中间情形，单位时间内上台面上被牵引而开始运动的链条的长度等于在下台面上堆积静止的链条的长度，此时链条的运动达到稳恒状态。这似乎是一个比较平庸的过程。不过可以稍作一些变化，考虑在两个台面之间的链条运动还存在一定的高度势垒，简单的情况即是链条置于位于上平台边沿的杯子中，链段之间未互相缠结，链条一端悬垂于杯子外，当其底端低于杯底一定程度或者给其施加向下的拉力时，链段在重力的作用下持续下落。大家可能会直观地认为在此过程中链条将贴杯子边沿往外补充，但通过简易的实验就会发现链条将跨过杯沿运动，链段在往外补充下落之前有一段悬空的部分，如图5(a)所示[21-22]。这一与直觉相左的悬空现象恰是它的迷人之处，这也就是2013年S. Mould在互联网上公布了该实验视频后点击量很快地飙升至数百万的原因(图5)。

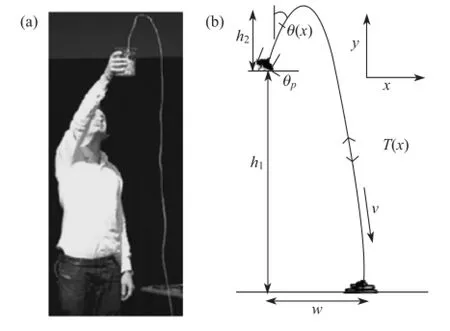
图5 链条悬空现象[22]：(a)S. Mould演示链条“喷泉”现象(J. Sanderson拍摄)；(b)链条的倒悬线轮廓

不过需要指出的是，S. Mould并非发现珠链悬空现象的第一人，事实上类似的现象已由M. G. Calkin在其1989年的另一篇文章[23]中做了描述。他研究的是悬吊于钉桩上的一根链条(如图6(a)所示)，当其一端运动下落时，由于链条的不可延展性，另一端将向上运动。链条的重力势能转化为其动能，链条被不断加速，在链条的弯折处由链条中的张力提供其向心力，当到达某一时刻时，向上运动的尾部链条的加速度和速度将大于向下运动的头部链条的加速度和速度，此时链条就将脱离钉桩并处于悬空状态(图6(b))，这类似于S. Mould在互联网上所展示的珠链“喷泉”(chain fountain)。

图6 悬吊于钉桩上的链条的下落运动示意图：(a)初始状态；(b) 下落一段距离后链条的悬空状态

在M. G. Calkin分析的这一物理过程中链条两端并未与任何平面接触。就我们所知，J. S. Biggins和M. Warner最先对位于两个台面之间的这一链条“喷泉”现象进行了分析和解释[22,24]。他们认为链条在运动过程中可以达到一个稳态，假设处于稳态时链条的运动速率为v，那么在dt时间内，将有质量为ρvdt的链段被拉起，其动量变化为dp=ρvdt·v，而根据动量定理，链段受力为f=v2。他们认为这一受力不单由链条中的张力提供，还由于台面上的静止链条对被拉起链段有一推力作用，并且说这一推力是形成链条“喷泉”的必要条件。他们通过简化的分析证明这一推力的存在是由于链条本身所具有的刚性导致链段被拉起时对剩余链条有一向下的作用力，因而其将受到向上的反作用力。J. S. Biggins指出当盛装链条的杯子倾斜使其底部与台面成一夹角时，链条“喷泉”的稳定轮廓为倒悬线型(图5(b))；而当杯子未倾斜时，链条“喷泉”是竖直的。当然这是在假设链条以垂直于杯底的方式被拉起的前提下分析得到的结果，而未考虑链条的实际堆积方式可能已使得链段与台面存在夹角，且在被拉起过程中链段并非是垂直于杯底。

由于在M. G. Calkin分析的系统中链条在其两端并未与任何平面接触的情况下依然能出现悬空现象，因此可以推断J. S. Biggins和M. Warner给出的链条“喷泉”的产生必须由杯底部产生推举链条向上的反常反作用而导致的解释并不确切(在两人的文章中还存在一些讹误)。当然这并非否认该反作用力的存在，实际上E. G. Virga用耗散冲击(dissipative shocks)来描述链条运动的文章[25]即假定杯底对珠链有冲击作用，从而改变链段的瞬时运动速率和方向，同样给出了J. S. Biggins和M. Warner业已给出的链条的倒悬线轮廓以及链条高于上平台的高度与上下平台之间的高度差成正比的结论。Virga在处理该问题过程中除了稳态条件并未引入过多的假设，因而其分析方法更显合理。

迄今为止仅有的关于链条“喷泉”的这三篇文献其关注的焦点主要在链条稳恒运动(在J. S. Biggins的文章[22]中稍涉链条“喷泉”形成与演化的分析)，在这一过程中沿链条的加速度为零。然而通过上两个部分的讨论我们知道，在初始阶段链条下落端尚未着地前，其运动满足初始堆积于平面上的链条下落的情况；而当最后阶段剩余链条长度基本与平台高度差相当时，其运动则类似于最终堆积于平面上的链条的下落(在链条转移的最后阶段，末端运动链节从杯中快速甩出，这一摆动可以看做是一个转动运动)。初始位于平面上的链条下落的加速度小于重力加速度g，最终位于平面上的链条下落的加速度则大于重力加速度g；而这里讨论的链条的下落包含了链条从较高的平面向较低台面的转移，实际上是上述两种情况的综合，对于在链条整个运动过程中其运动状态的转变(尤其是加速度的变化)的理解是认识链条“喷泉”现象的关键。

5 结语

通过上述讨论，我们不难发现，即使是对于下落链条这样看似简单的力学体系，确切的认识也并非是一步到位的，以往的研究中不乏这样那样的错误。我们在向公众演示链条“喷泉”现象并与之进行讨论的过程中，发现在大家的认识空间中存在着一些知识误区或盲区；而此前在阅读相关文献的过程中，也发现一些文献中的讨论并不能让人信服。我们在此不恤分享自己的一些浅陋认识，以期提请大家注意链条下落运动的复杂性以及可能导致的一些认识误区。

对于下落运动这样常见的体系，由于教科书中的简化处理，往往造成我们在头脑中形成错误的印象，而忽略了其背后的深刻内涵(我们必须认识到这一点：物理学的基本规律是可以进行简单表述的，但是物理学的认识对象却是纷繁复杂的。否则会对物理学产生错误的印象，即认为物理学关注的仅仅是从复杂到简单的归纳过程。这代表了物理学的一部分，但并非全部)。在本文开篇已经提到，物理学的几个重大发展都离不开对下落运动的深刻理解。另外从现象学的角度来看，下落运动也包含了丰富有趣的内容，例如下落体形状对于运动的影响(譬如落叶的运动描述)，以及下落对于物体形状的影响。从上文的讨论也可以看到，对于同一运动物体，设定条件的差异会带来截然不同的运动现象。不同下落体(固体球、液滴、链条、颗粒物)与接触平面(液面、固体平面、颗粒堆积物表面)的相互作用会带来许多复杂的(非线性)运动行为，对这些现象的理解可以大大地帮助我们认识许多真实的自然现象(如星体表面撞击坑的成因、降雨等)和生产生活现象(如喷灌)。本文介绍的链条下落运动只是冰山一角，然而已经表现出如此多的出人意料，并且还有许多细节有待于深入探究，本文权作引玉之砖。

(2014年10月15日收稿)

[1] HEILBRON J L. Galileo [M]. New York: Oxford University Press, 2010.

[2] ANDRADE E N Da C. Isaac Newton [M]. London: Max Parrish, 1950.

[3] PAIS A. Subtle is the Lord: the science and the life of Albert Einstein [M]. New York: Oxford University Press, 1982.

[4] GALILEI G. Discorsi e dimostrazioni matematiche intorno a due nuove scienze attenenti alla meccanica e i movimenti locali [M]. Leiden: Elsevier, 1638.

[5] VILLAGGIO P. Mathematical models for elastic structures [M]. Cambridge: Cambridge University Press, 1997.

[6] HOOKE R. A description of helioscopes, and some other instruments [M]. London: John Martin, 1676.

[7] EscherMath. The geometry of antoni gaudi [EB/OL].(2012-8-15) [2014-10-14]http://euler.slu.edu/escher/index.php/The_Geometry_of_ Antoni_Gaudi.

[8] SHARLIN H I, SHARLIN T. Lord Kelvin: the dynamic victorian [M]. Pennsylvania: Pennsylvania State University Press, 1979.

[9] AIRY G B. On the mechanical conditions of the deposit of a submarine cable [J]. Philosophical Magazine, Series 4, 1858, 16(104): 1-18.

[10] BELETSKY V V, LEVIN E M. Dynamics of space tether systems [M]. San Diego: American Astronautical Society, 1993.

[11] ZHANG X, YULONG L, LIU Y Y, et al. Arresting hook and cable dynamics of aircraft arrest landing on or off center [J]. Journal of Mechanical Strength, 2008, 30: 549-554.

[12] CALKIN M G, MARCH R H. The dynamics of a falling chain: I [J]. American Journal of Physics, 1989, 57: 154-157.

[13] SCHAGERL M, STEINDL A, STEINER W, et al. On the paradox of the free falling folded chain [J]. Acta Mechanica, 1997, 125: 155-168.

[14] TOMASZEWSKI W, PIERANSKI P. Dynamics of ropes and chains: I. the fall of the folded chain [J]. New Journal of Physics, 2005, 7: 45.

[15] WONG C W, YASUI K. Falling chains [J]. American Journal of Physics, 2006, 74: 490-496.

[16] CAYLEY A. On a class of dynamical problems [J]. Proceedings of the Royal Society of London, 1857, 8: 506-511.

[17] WONG C W, YOUN S H, YASUI K. The falling chain of Hopkins, Tait, Steele and Cayley [J]. European Journal of Physics, 2007, 28: 385-400.

[18] SOMMERFELD A. Lectures on theoretical physics, volume 1, mechanics [M]. New York: Academic Press, 1964.

[19] GREWAL A, JOHNSON P, RUINA A. A chain that speeds up, rather than slows, due to collisions: How compression can cause tension [J]. American Journal of Physics, 2011, 79: 723-729.

[20] HAMM E, GÉMINARD J C. The weight of a falling chain, revisited [J]. American Journal of Physics, 2010, 78: 828-833.

[21] MOULD S. Self siphoning beads [EB/OL]. [2013-10-14]http:// stevemould.com/siphoning-beads/.

[22] BIGGINS J S. Growth and shape of a chain fountain [J]. EPL, 2014, 106: 44001-1-6.

[23] CALKIN M G.The dynamics of a falling chain: II [J]. American Journal of Physics, 1989, 57: 157-159.

[24] BIGGINS J S, WARNER M. Understanding the chain fountain [J]. Proceedings of the Royal Society A, 2014, 470: 2163.

[25] VIRGA E G. Dissipative shocks in a chain fountain [J]. Physical Review E, 2014, 89: 053201-1-9.

Motions of a falling chain: A brief analysis

YU Tong-xu, ZHANG Wen-bin, XU Teng, CAO Ze-xian
Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China

Mechanical analysis involving chains is a very interesting topic that has drawn much attentions in history. As a characteristic variable-mass system, a falling chain is often referred as an example in textbooks of mechanics. However, there are many inconsistencies in the treatment of falling motions of the flexible chain, which demand to be clarified. The falling motion behavior depends critically on the initial configurations of the chain. In the present article we are concerned with four distinct setups, of which the diverse motion behaviors will be briefly analyzed.

falling chain, variable-mass system, acceleration, piling configuration, geometrical profile

(编辑：段艳芳)

10.3969/j.issn.0253-9608.2015.01.008

†通信作者，E-mail：yutongxusf03@iphy.ac.cn