基于平面连杆机构的周转轮系设计与计算*
2015-05-11宋莹
宋 莹
(宁夏工商职业技术学院,宁夏银川 750021)
0 引言
周转轮系广泛应用于各种机械中,然而传统的组合方法却难以获得更多新型的周转轮系。而基于单铰运动链的型数综合虽可以得到许多不同功能的连杆机构,但连杆机构的局限性又致使其在实际应用中受到限制[1]。以十二杆单铰运动链为例,展示了如何基于平面连杆机构转化为周转轮系的推理过程,为新型周转轮系的获取提供了实例验证。
1 单铰运动链中各元素杆组成分析与计算
在单铰运动链中,有且仅有几个转动副的杆即为几元素杆。对于十二杆单铰运动链,由于一个构件的运动副的元素数Jm满足Jm≤N/2(N为构件数),因此,十二杆单铰运动链中最多为6元素杆,即有且仅有6个转动副,用N6表示,其它各元素杆的表示依此类推。按单铰运动链基本结构公式,可知:

式中:F为自由度。
考虑自由度F=1,则方程组(1)可改写为:
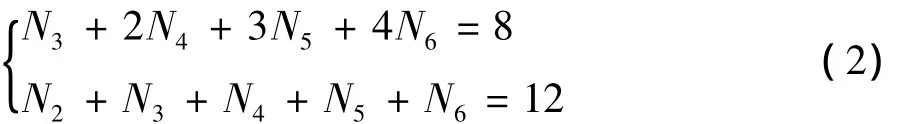
由N3+2N4+3N5+4N6=8可得N3+2N4+3N5=8-4N6,且由于 N3、N4……N6等均为非负整数,则 8-4N6≥0,则 N6≤2,即 N6只可以取为 2、1、0 三个数。同理,可确定N5只可以取为2、1、0;N4只可以取为4、3、2、1、0;N3只可以取为 8、7 …… 1、0 九个数。
考虑求解过程中各种情况分类的规律性,故以N6为起点。确定N6后再依次考虑N5、N4等,这样可以避免分类求解过程中出现遗漏解和重复解。
(1)N6=2
可确定N3+2N4+3N5=0,则N3=N4=N5=0,从而可知N2=10。
综上,在N6=2时,可得一组解:N2=10、N3=N4=N5=0、N6=2。
(2)N6=1
可确定N3+2N4+3N5=4,由上述方法可知,N5此时只能取为1和0。
当N5=1时,N3+2N4=1,此时N4只能取为0,则N3=1、N2=9;
当N5=0时,N3+2N4=4,此时N4只可以取为2、1、0,再按与处理N5同样的方法考虑N4。依次类推下去可获得此情况下全部解为:

综上,在N6=1时,可得四组解:
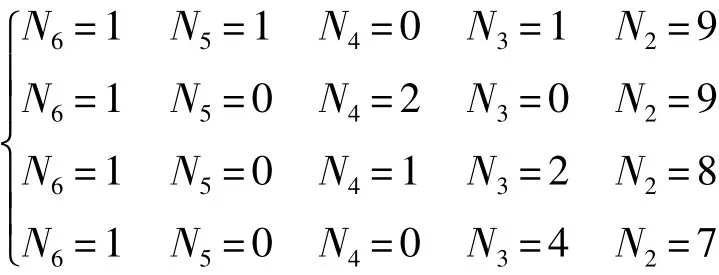
(3)N6=0
同理,采用(2)中所采用的方法进行求解,在N6=0时,可获得如下十组解:
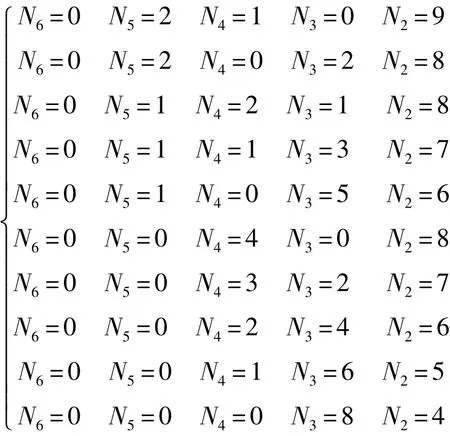
2 胚图、环路图和单铰运动链的确定
任取上述方程组的一组解:N6=1,N5=0,N4=0,N3=4,N2=7,以此为例,采用环路图法对胚图、环路图和单铰运动链进行确定[2-3]。在环路图法中,“点”代表构件,“线”代表运动副。
(1)胚图的确定。所谓胚图,即先将表示二元素杆以上的多元素杆的“点”放在环路上。很显然,代表几元素杆的“点”自然对应于几条“线”。胚图类型有多种,所作图1仅为其中一种而已。
(2)环路图和单铰运动链的确定。将表示二元素杆的点合理地分布到胚图的环路上。分布时,应使胚图的每个环路上至少有4个构件,以保证后续啮合齿轮高副可顺利替代二元素杆。如图2为环路图。依据此环路图即可确定相应的单铰运动链,如图3。
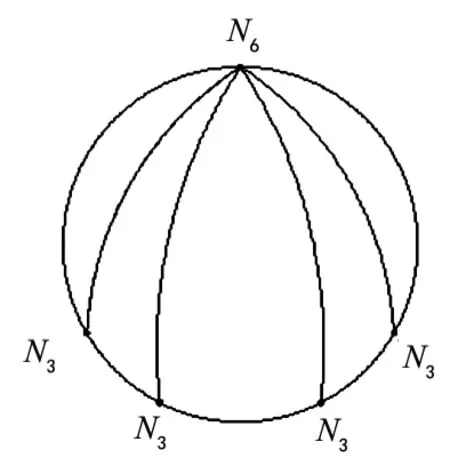
图1 胚图
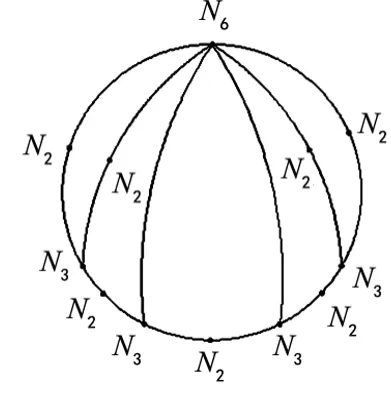
图2 环路图
3 单铰向复铰的演化
单铰向复铰的演化是基于二元素杆以上的多元素杆的单边局部收缩来实现的,所谓局部收缩是指为了不减少单铰运动链的构件数,多元素杆可收缩的边数只能小于其单铰数。一般情况下,单铰运动链中的回路不都是四杆回路,而齿轮啮合高副只能处于四杆回路中。通过多元素杆局部收缩的方法可使单铰运动链中五杆及其以上的回路变为四杆回路,从而实现单铰向复铰的演化[4-5]。如图4所示。
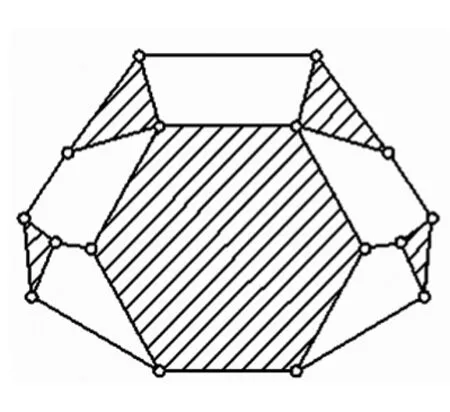
图3 单铰运动链

图4 复铰运动链
在复铰运动链图中,以小写字母标出将被啮合齿轮副替代的二元素杆,以阿拉伯数字对真实杆进行编号。四杆回路以RRBB表示,四杆包括一个将被啮合齿轮副替代的二元素杆和三个真实杆。其中,B-B为被替代的二元素杆,B相当于啮合齿轮齿廓的曲率中心,R相当于啮合齿轮转动中心,B必须是单铰,R可以是单铰,也可以是复铰。
4 周转轮系机构简图的生成
由图4可知,杆2、杆5和其中之一连杆R-R构成复合铰链,杆3、杆5和另一连杆R-R也构成复合铰链。在生成周转轮系结构时,杆2、3、5应转化为同轴齿轮,两R-R连杆转化为行星架。杆1和杆4转化为行星轮,a、b、c、d、e二元素杆最终被啮合齿轮副替代。周转轮系机构简图如图5所示。
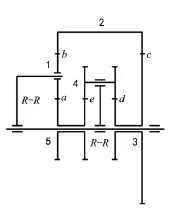
图5 周转轮系机构简图
5 结语
基于单铰运动链的型数综合,可获得大量的异构单铰运动链,在此基础上很容易处理得出许多具有不同功能的平面连杆机构。通过上述对十二杆单铰运动链转化为周转轮系过程的实例验证,可知,基于平面连杆机构容易转化获得相应的周转轮系,这为开发设计周转轮系提供了另外一种途径,具有一定的工程实际意义。
[1] 韩建友,杨 通,于靖军.高等机构学[M].北京:机械工业出版社,2015.
[2] 冯 俊.单铰运动链的型综合及机械运动方案创新设计方法研究[D].重庆:重庆大学,2007.
[3] 丁华峰.运动链的环路理论与同构判别及图谱库的建立[D].秦皇岛:燕山大学,2007.
[4] 安培文,黄茂林.基于单铰运动链的周转轮系创新综合方法[J].机械设计与研究,2001,3(1):41-45.
[5] 梁云峰,谷凤民.基于十二杆单铰运动链的周转轮系综合方法[J].重庆科技学院学报,2008,2(1):52-54.
