混合钢U肋加劲板焊接残余应力影响因素分析

赵 秋， 郭智勇， 袁辉辉， 陈美忠

(福州大学土木工程学院， 福建 福州 350116)

混合钢U肋加劲板焊接残余应力影响因素分析

赵 秋， 郭智勇， 袁辉辉， 陈美忠

(福州大学土木工程学院， 福建 福州 350116)

建立三维热弹塑性有限元模型， 对混合钢U肋加劲板的焊接温度场和应力场进行模拟， 并应用盲孔法残余应力测试试验验证了该数值模拟方法的正确性. 应用经验证的焊接残余应力数值模拟方法， 研究散热系数、 焊接有效功率、 熔池面积大小、 焊接速度变化对混合钢U肋加劲板焊接残余应力分布与大小的影响. 结果显示， 焊接有效功率对混合钢U肋加劲板的残余应力分布的影响最大， 其次为熔池面积及焊接速度， 散热系数影响很小； 母板和U肋的残余拉应力和残余压应力大小、 残余拉应力区分布宽度、 母板残余拉应力合力和残余压应力合力， 与焊接有效功率和熔池面积大小成正比变化， 与焊接速度成反比变化； 而U肋残余拉应力合力和残余压应力合力， 与焊接有效功率成正比变化， 与熔池面积大小和焊接速度成反比变化.

钢桥； 焊接残余应力； 热弹塑性； 有限元模拟； 混合钢U肋加劲板

0 引言

带U肋的加劲板是桥梁钢箱梁顶底板的主要受力构件. 如U肋与母板采用不同强度等级的钢材进行设计， 可提高材料的使用效率， 这样的加劲板称为混合钢U肋加劲板. U肋与母板连接处在电弧焊接过程中， 由于局部急剧加热使得焊缝及其附近区域的温度分布极不均匀， 焊接过程中不可避免要产生残余应力[1]. 为了解焊接残余应力对结构受力性能的影响， 研究者采用多种试验方法来预测焊接结构的残余应力分布， 如X射线法、 磁测法、 切条法、 盲孔法等[2-5]. 随着应用有限元方法的计算机技术的进步， 可以借助数值模拟技术分析焊接结构中残余应力分布[6-9]. 但在数值模拟过程中， 一些参数的选取往往会对残余应力分布产生较大影响. 因此， 本研究首先采用较为精确的盲孔法验证混合钢U肋加劲板的数值模拟方法的正确性， 再研究数值模拟相关参数对混合U肋加劲板焊件纵向残余应力分布与大小的影响， 从而为得到较为精确的数值模拟结果提供依据.

1 盲孔法残余应力试验验证

1.1 试件设计

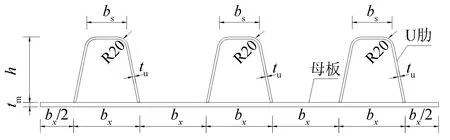
图1 残余应力测试试件断面图(单位： mm )

在钢箱梁的顶、 底板上， 横桥向选取含有3个U肋的加劲板作为试验构件进行残余应力分布试验， 试件尺寸由实桥按1 ∶2.5比例缩尺得到， 缩尺后试件尺寸如图1和表 1所示. 试件长度为600 mm. 试件考虑了U肋加劲板按混合钢设计时U肋与母板的3种强度组合情况.

表1 试件主要参数表

1.2 有限元模型

利用试件的对称性对有限元模型进行简化， 模型可采用1个U肋与其相邻的母板的一半， 根据文献[10]试件长度取150 mm， 焊缝构造按图2要求建立. 为精准模拟混合钢U肋加劲板的焊接残余应力场， 采用ANSYS有限元软件建立考虑热弹塑性的三维有限元模型， 采用生死单元法模拟焊缝填充和焊接热输入过程， 对混合钢U肋加劲板的焊接温度场和应力场进行模拟， 有限元模型如图3所示. 热源移动速度为10 mm·s-1， 时间步长为0.2 s， 试件最后冷却至室温状态. 数值模拟中， 忽略熔池内部化学反应， 焊接电流、 电压及速度为恒定值. 其它有关数值模拟未说明情况参照文献[10].

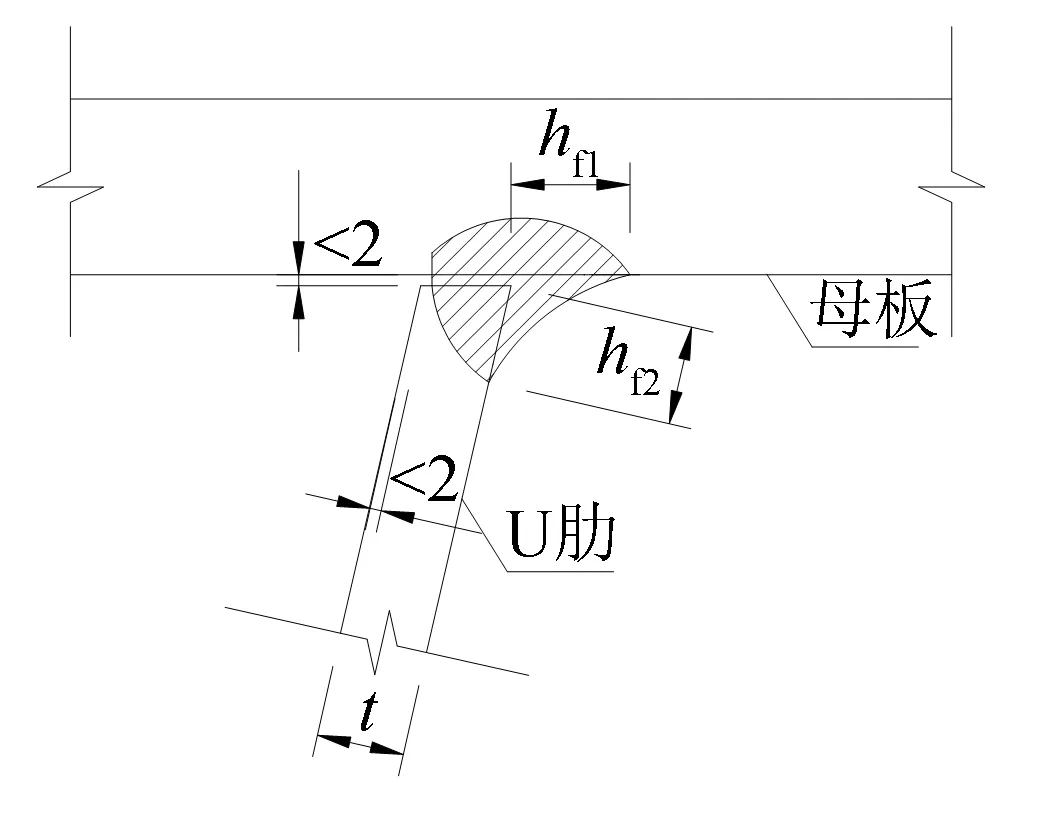
图2 U肋加劲板焊缝示意图(单位： mm)

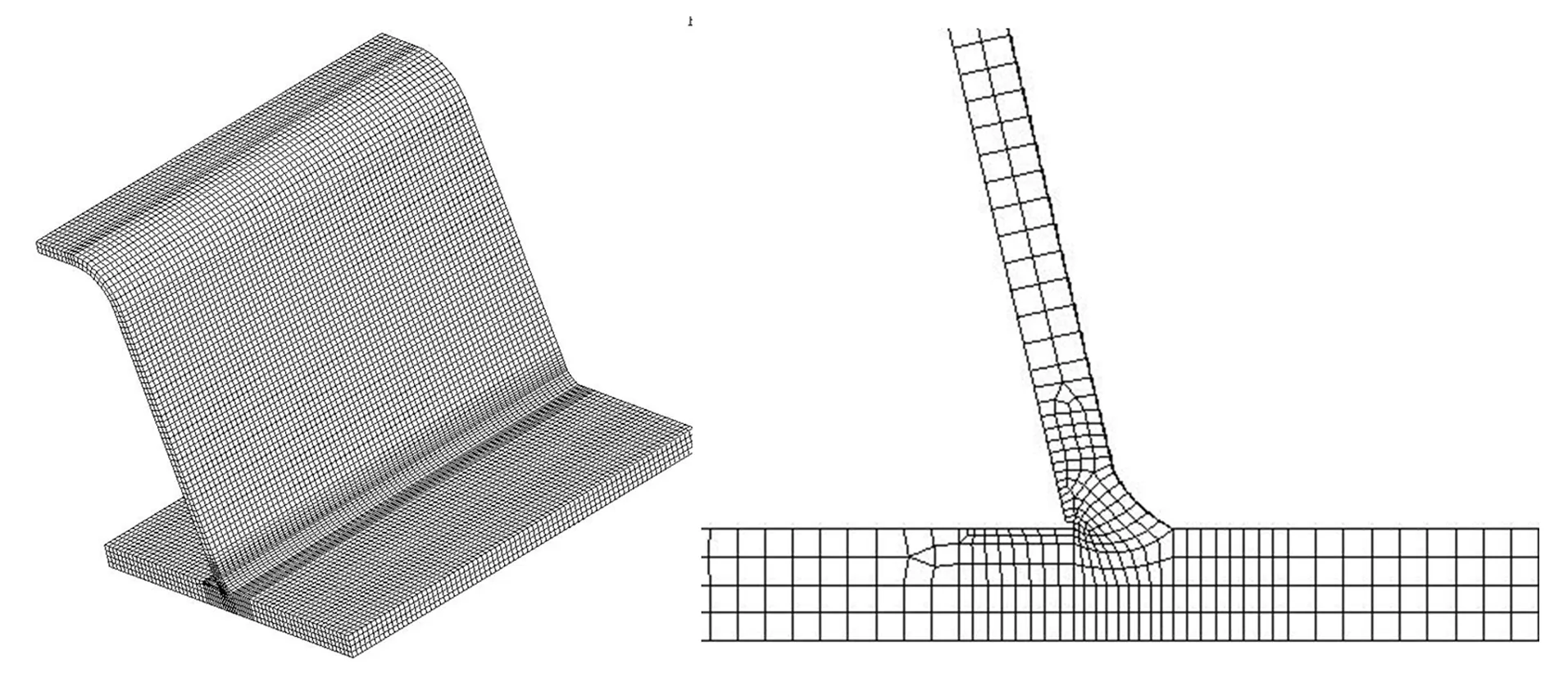
图3 有限元模型网格划分

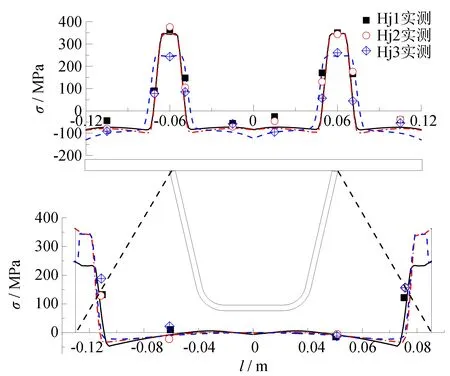
图4 焊接残余应力实测值与理论计算值比较

1.3 残余应力结果验证

采用盲孔法对混合钢U肋加劲板进行残余应力测试， 测点残余应力平均值与有限元模拟结果如图4所示. 由图4可以看出， 有限元模拟结果与试验所得残余应力测试值基本相吻合， 并补充了试验测点间的残余应力分布趋势， 验证本文所用数值模拟方法的正确性.

2 影响因素分析

2.1 散热条件变化对残余应力分布的影响

散热条件是指焊接过程中结构表面边界的热损失情况， 包括对流与辐射换热. 为方便计算， 引用一个总传热系数β，β=βc+βe， 其中：βc为对流换热系数，βe为辐射换热系数. 由于操作在室内进行， 取传热系数βe为13W·(m2·K)-1， 在所有外表面均施加换热边界条件. 以试件Hj1为基础(母板为Q345，U肋为Q235， 后续分析中相同)， 分析散热系数变化对残余应力分布影响如图5所示， 图中1.0β为实际环境下的散热系数， 0.8β为当前散热系数的0.8倍， 1.2β为当前散热系数的1.2倍. 从图5可以看出， 随着散热系数由0.8β增大至1.2β， 母板和U肋的残余应力分布基本不变.

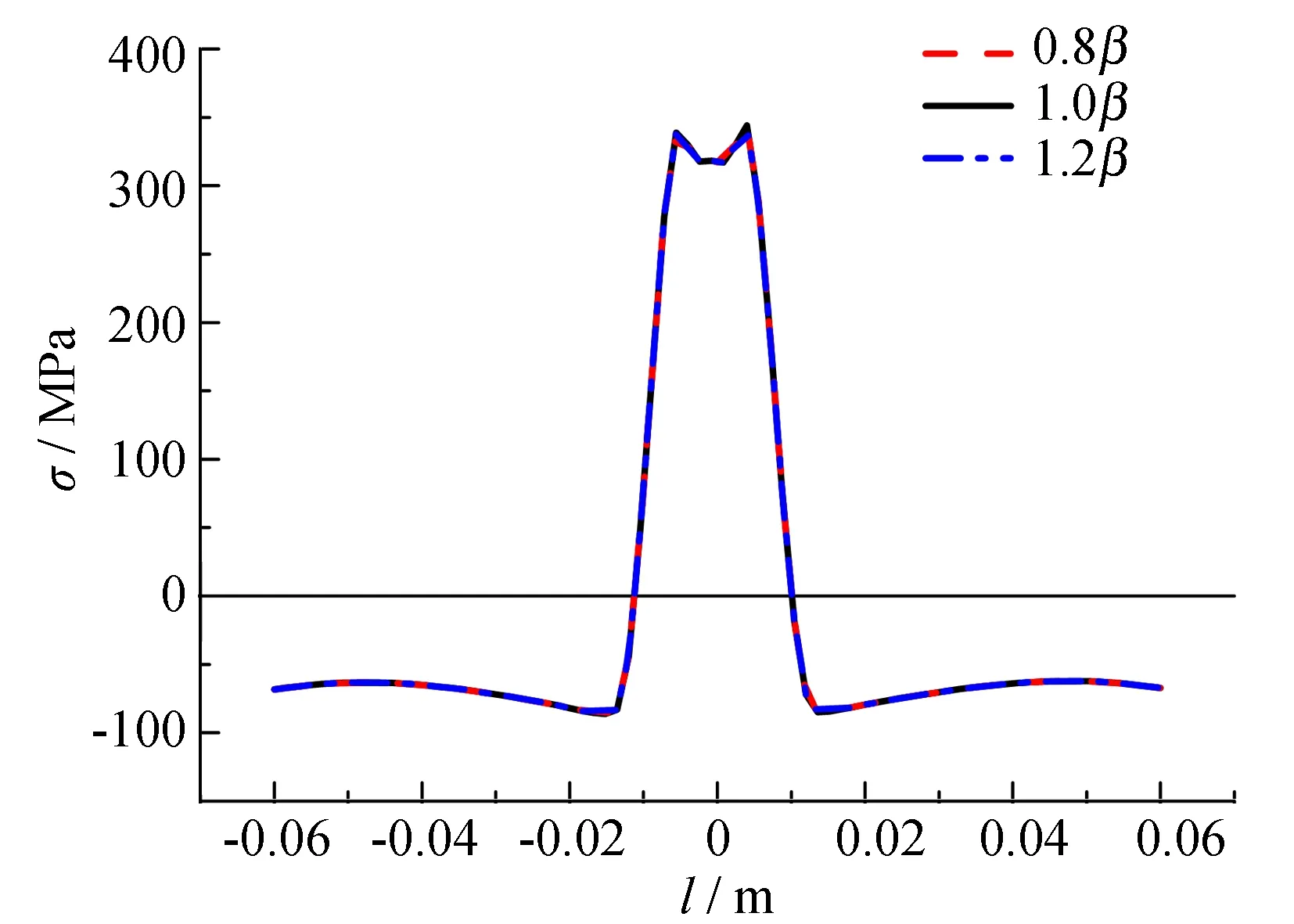
(a) 母板残余应力分布

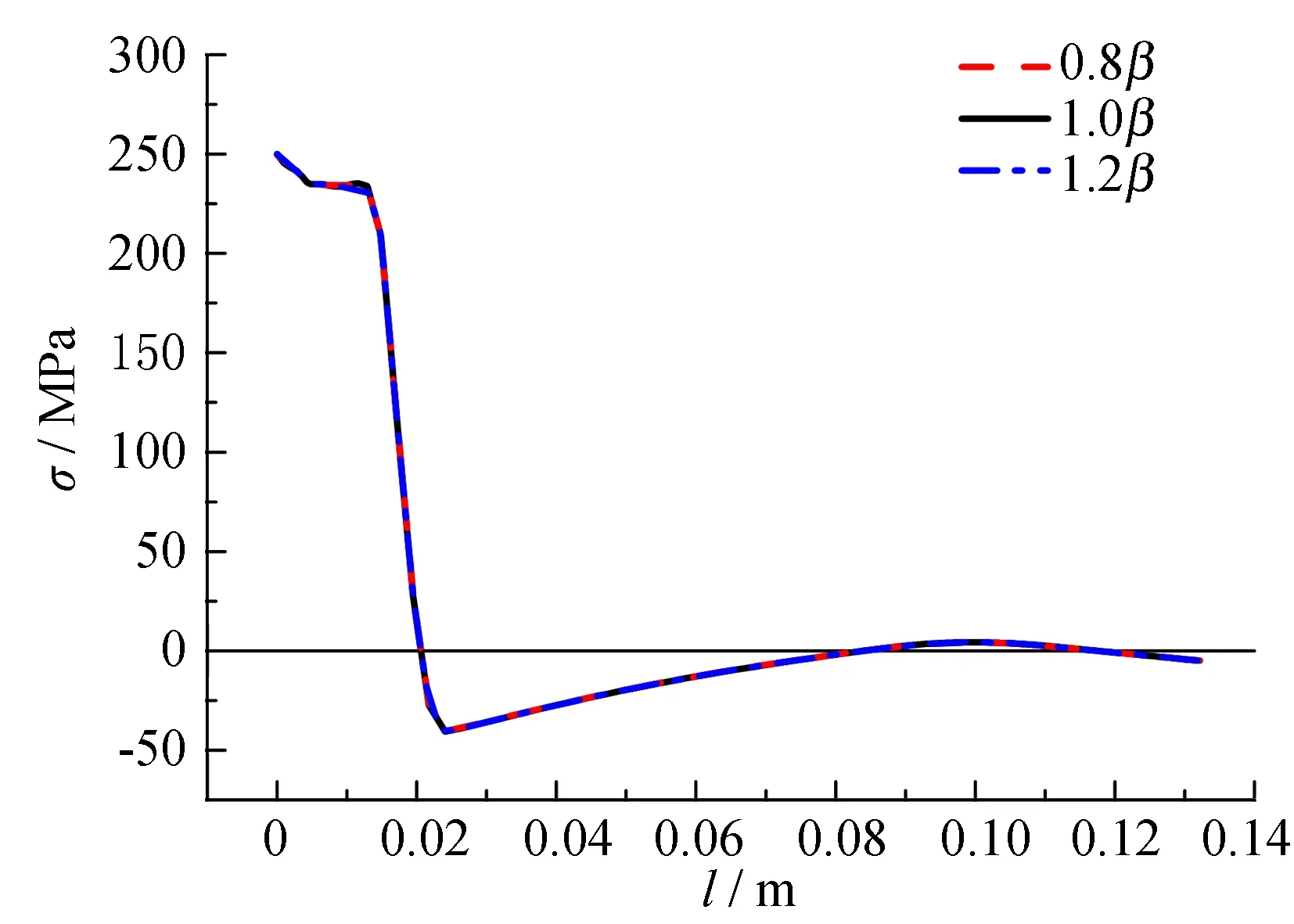
(b) U肋残余应力分布

2.2 焊接有效功率对焊接残余应力分布的影响

焊接有效功率的大小是决定焊接温度场及焊接应力场分布的主要因素之一. 在数值模拟中， 每个载荷施加的生热率如下：

式中：Q为焊接电弧的有效功率， W；I为焊接电流， A；U为焊接电压， V；η为焊接热效率；Aweld为焊缝的横截面积， m2；v为焊接速度， m/s. 由公式(1)可以看出， 焊接有效功率大小由焊接电流、 电压和热效率决定. 由于单独分析焊接电流、 电压和热效率对残余应力分布的影响， 与分析有效功率的效果相同， 故本文不再单独分析焊接电流、 电压和热效率的影响. 有效功率变化对残余应力分布影响如图6所示， 图中1.0Q为实际焊接有效功率， 0.8Q为有效功率的0.8倍， 1.2Q为有效功率的1.2倍. 从图6可以看出， 随着焊接有效功率值由0.8Q增大至1.2Q， 母板残余拉应力峰值相对增大13%， 残余拉应力分布宽度相对增大24%， 残余压应力绝对值相对增大20%； U肋残余拉应力峰值相对增大4%， 残余拉应力分布宽度相对增大18%， 残余压应力峰值绝对值相对增大28%.

图7和图8分别为残余拉、 压应力合力和合力分配比例随有效功率增加变化曲线. 从图7和图8可以看出， 随着焊接有效功率的增大， 母板残余拉应力的合力和残余压应力的合力随之明显增大， U肋残余拉应力的合力和残余压应力的合力增加较小. 从分配比例来看， 母板残余拉应力和残余压应力的合力比例增大， 而U肋上的残余拉应力和残余压应力的合力比例减小.

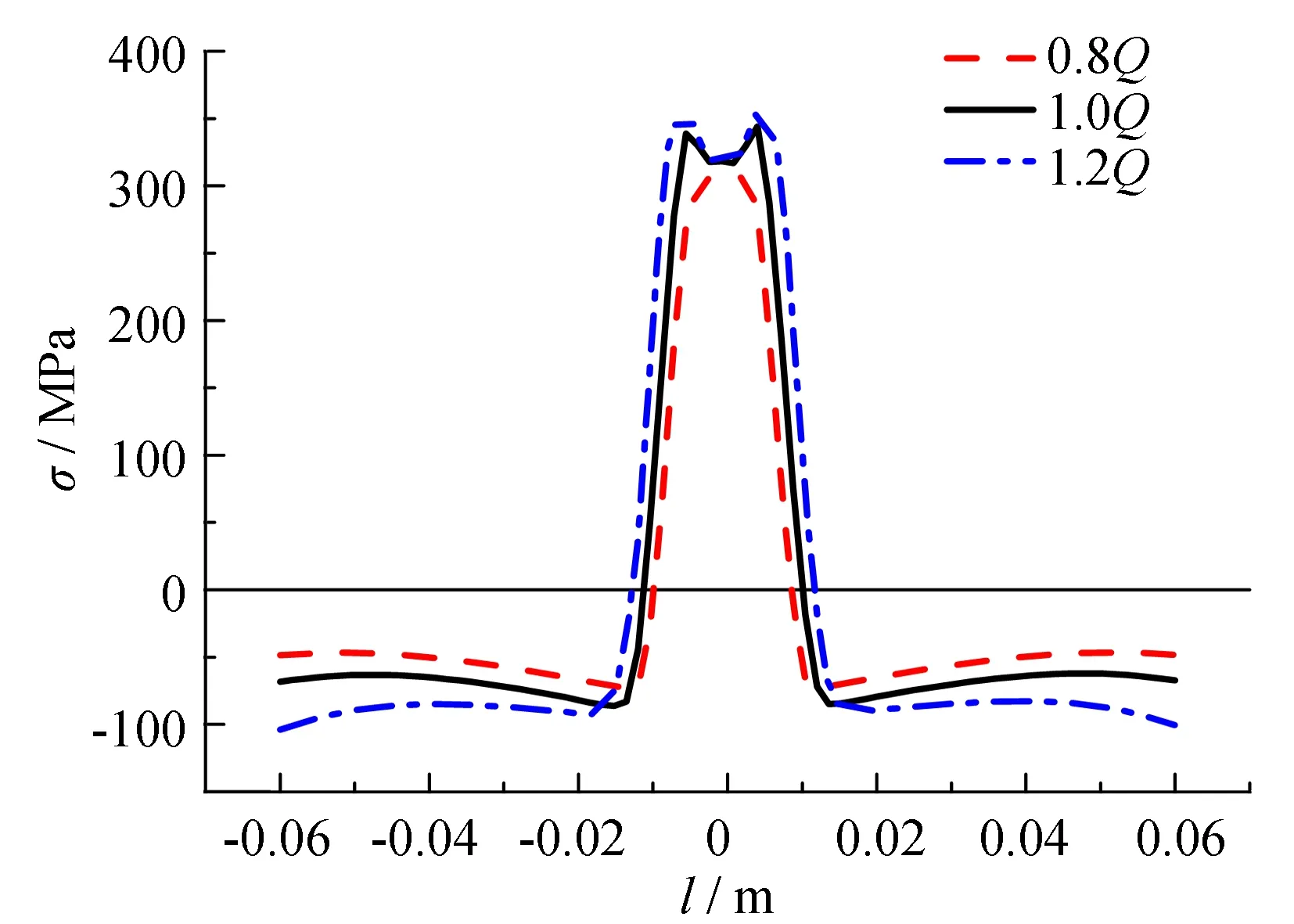
(a) 母板残余应力分布

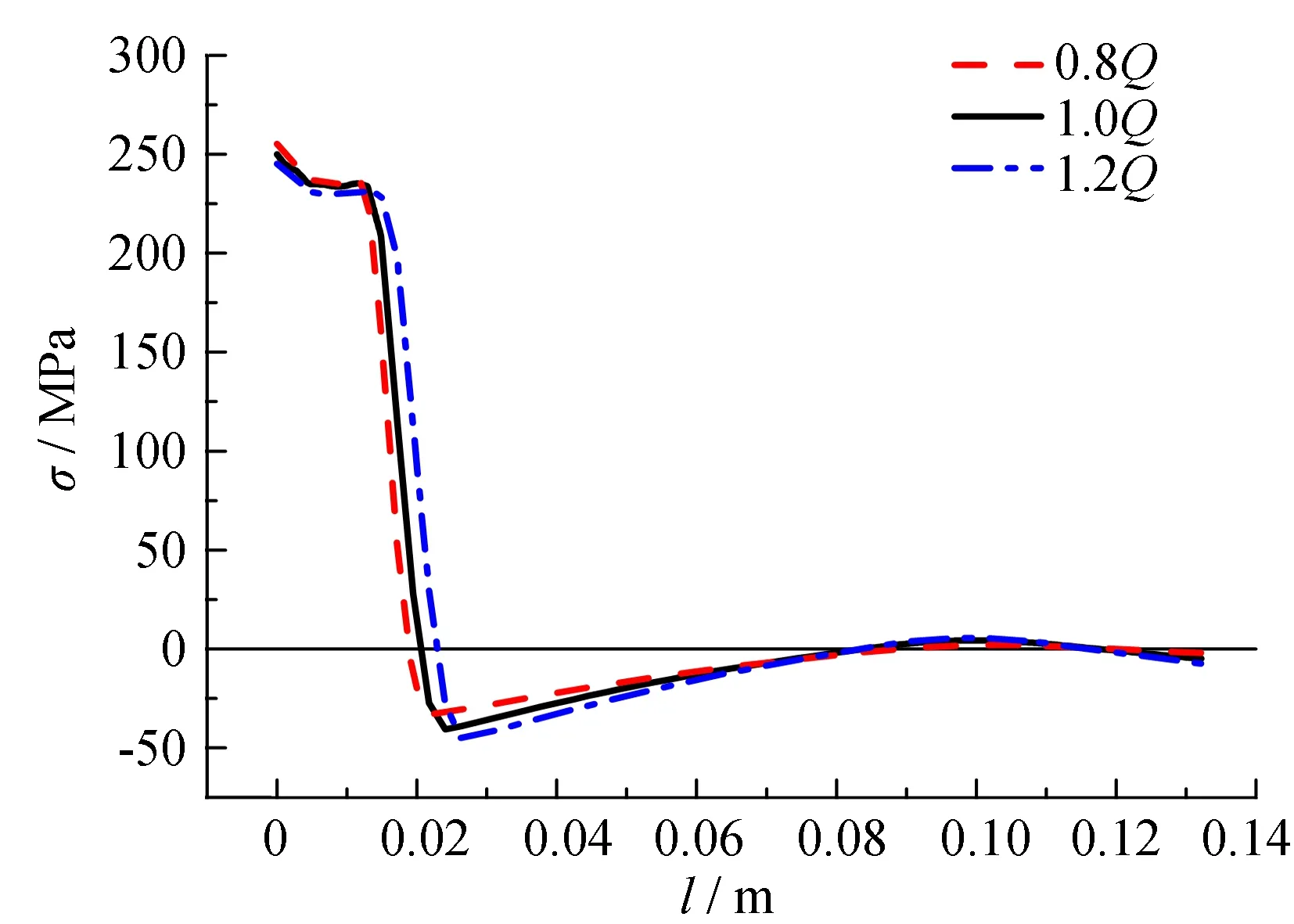
(b) U肋残余应力分布

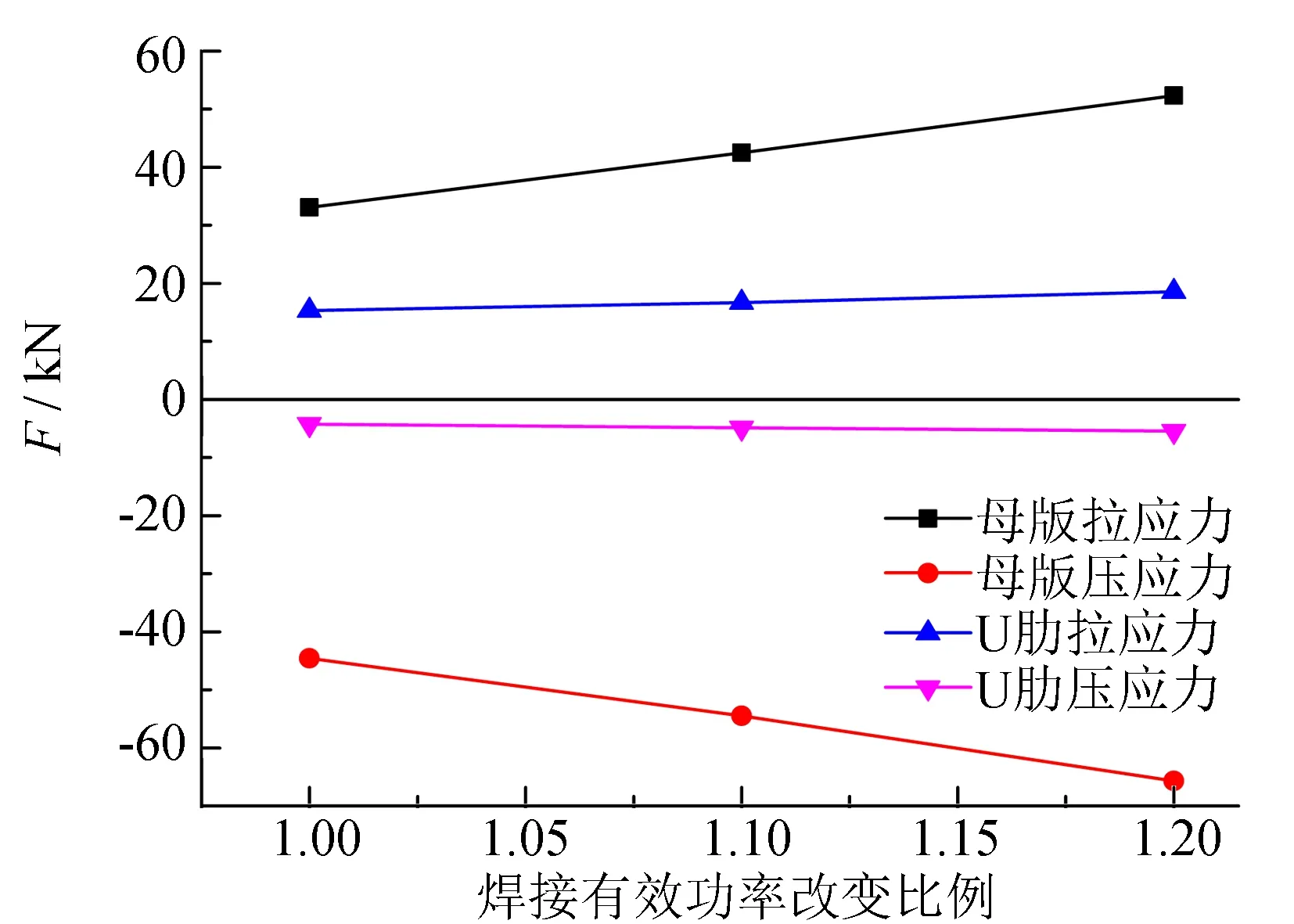
图7 不同焊接有效功率下的残余应力合力变化

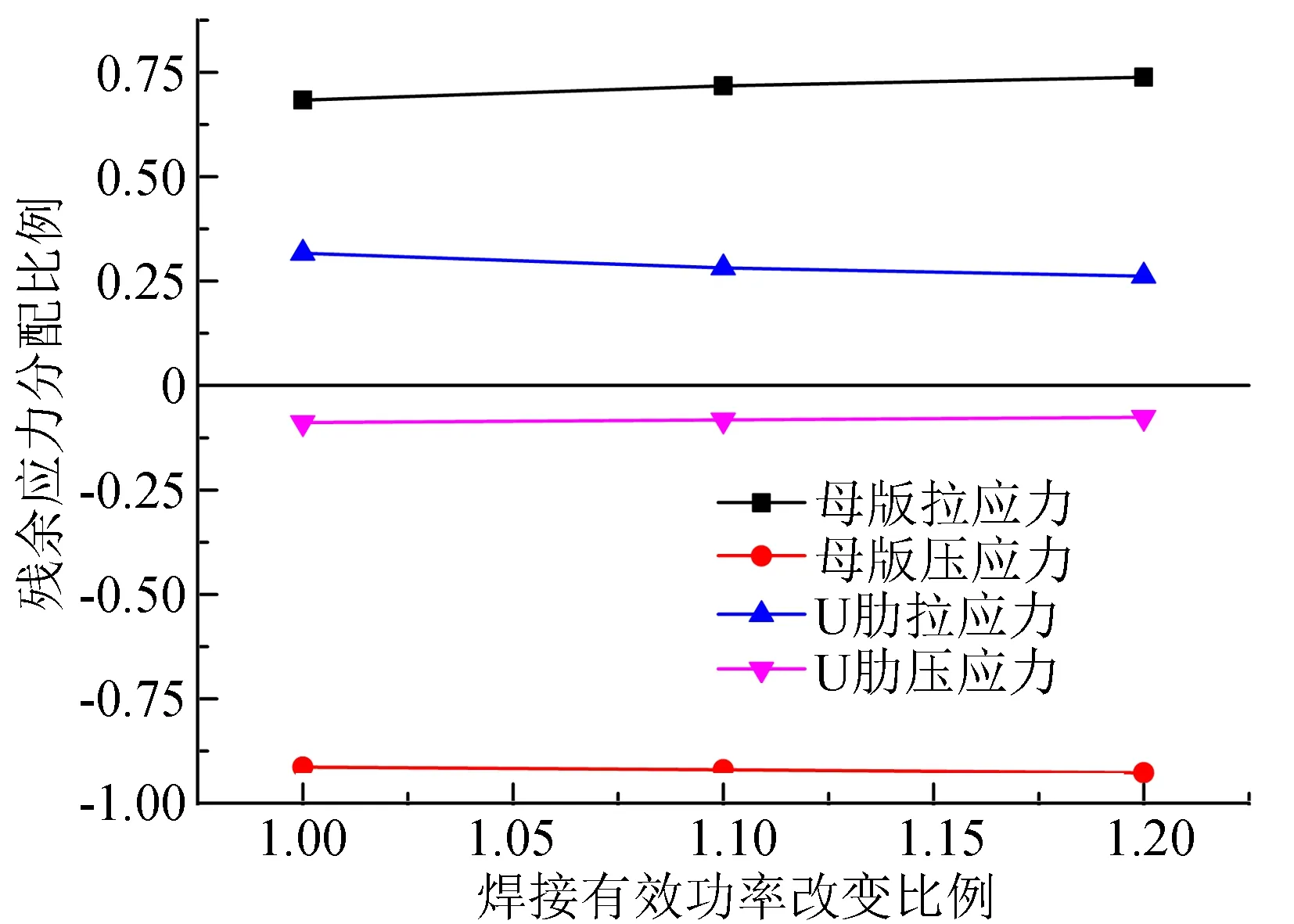
图8 不同焊接有效功率下的残余应力合力分配比例变化

2.3 熔池面积大小对残余应力分布的影响

熔池面积的大小主要是由焊脚尺寸以及熔深决定的， 焊脚尺寸决定焊缝熔池的宽度， 熔深影响沿板厚方向熔池的大小. 熔池面积影响焊接热输入大小， 进而影响焊接温度场、 焊接应力场和最终的残余应力分布. 熔池面积(S)变化对残余应力分布影响如图9所示.

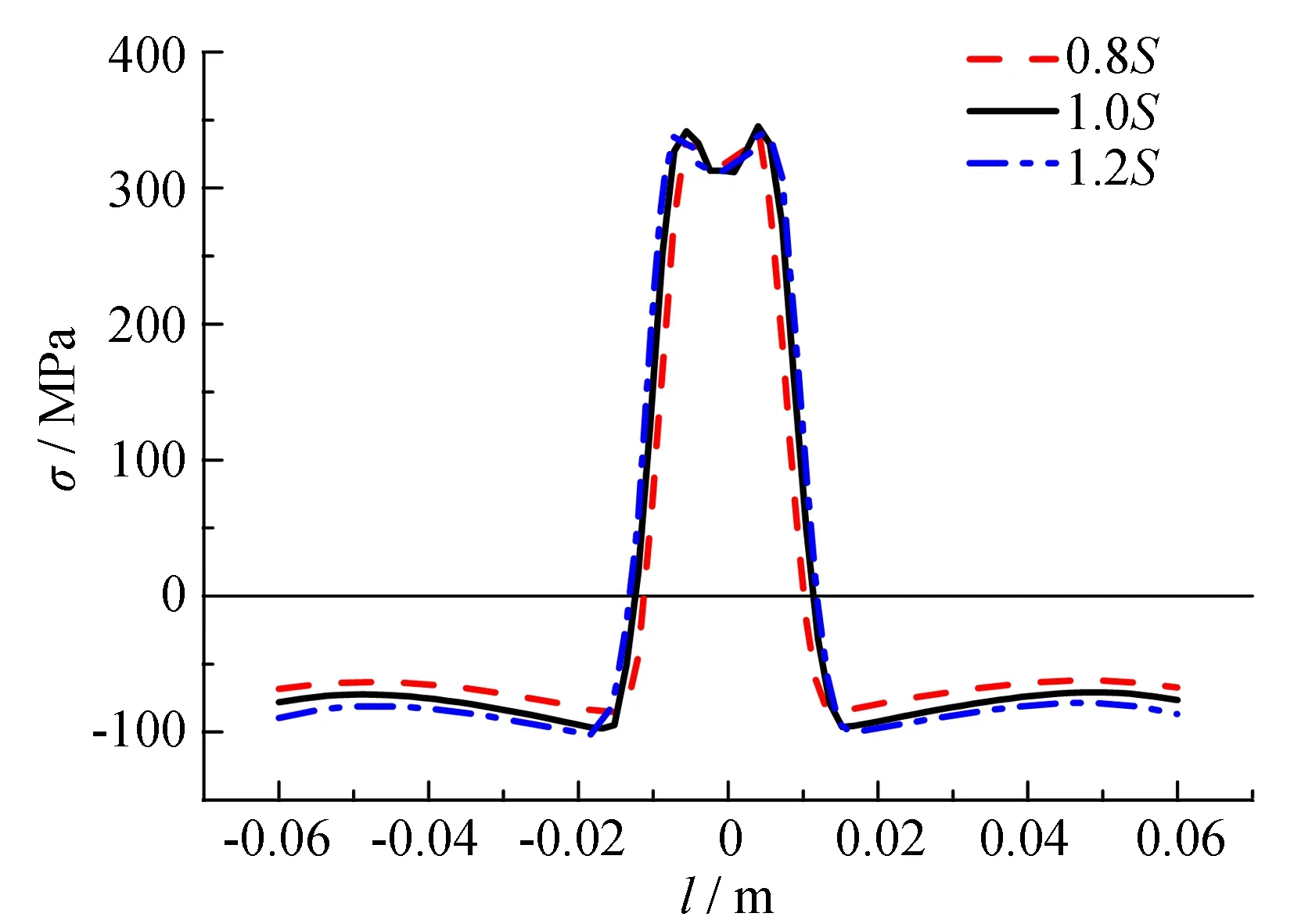
(a) 母板残余应力分布

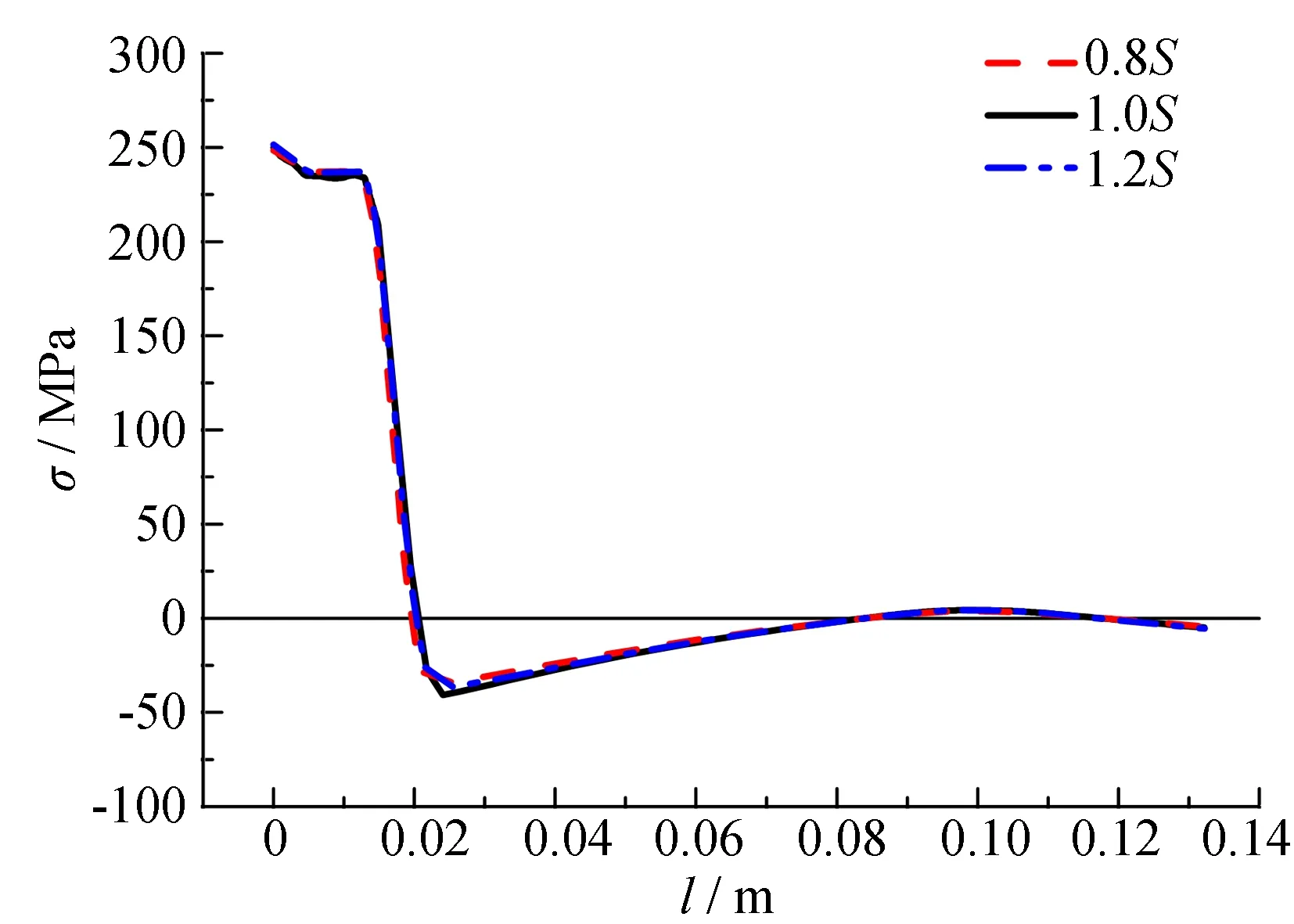
(b) U肋残余应力分布

图9中1.0S为基准焊缝熔池面积， 0.8S为基准熔池面积的0.8倍， 1.2S为基准熔池面积的1.2倍. 从图9可以看出， 随着熔池面积系数由0.8S增大至1.2S， 母板残余拉应力峰值相对增大3%， 残余拉应力分布宽度相对增大15%， 残余压应力绝对值相对增大18%； U肋残余拉应力峰值相对增大2%， 残余拉应力分布宽度相对增大6%， 残余压应力峰值绝对值相对增大19%.

不同熔池面积下的母板和U肋残余应力合力和合力分配比例如图10、 11所示. 从图10、 11中可以看出， 随着混合钢U肋加劲板熔池面积的增大， 母板残余拉应力的合力和残余压应力的合力随之明显增大， U肋残余拉应力的合力和残余压应力的合力略微减小. 从分配比例来看， 母板残余拉应力和残余压应力的合力比例增大， 而U肋上的残余拉应力和残余压应力的合力比例减小.

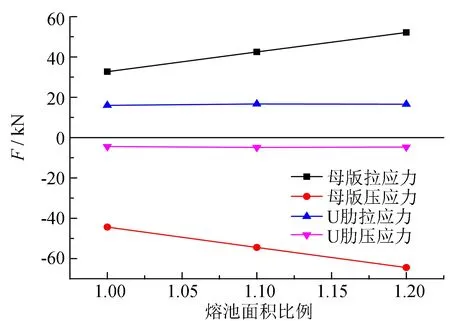
图10 不同熔池面积下的残余应力合力

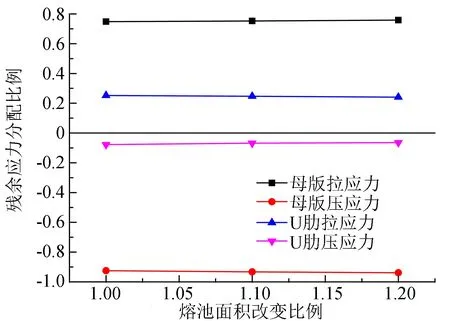
图11 不同熔池面积下的残余应力合力分配比例变化

2.4 焊接速度对残余应力分布的影响

在单位时间内， 不同的焊接速度将导致焊缝热流量的不同， 从而造成温度梯度不同， 最终影响焊接温度场和应力场的分布. 焊接热源移动速度(v)变化对残余应力分布影响如图12所示. 图中1.0v为焊接热源移动速度， 0.8v为当前焊接热源移速的0.8倍， 1.2v为当前焊接热源移速的1.2倍. 从图12可以看出， 随着热源移动速度由0.8v增大至1.2v， 母板残余拉应力峰值相对减小6%， 残余拉应力分布宽度相对减小20%， 残余压应力绝对值相对减小7%； U肋残余拉应力峰值相对减小4%， 残余拉应力分布宽度相对减小9%， 残余压应力峰值绝对值相对减小13%.

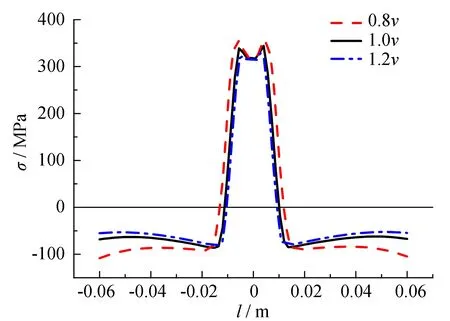
(a) 母板残余应力分布

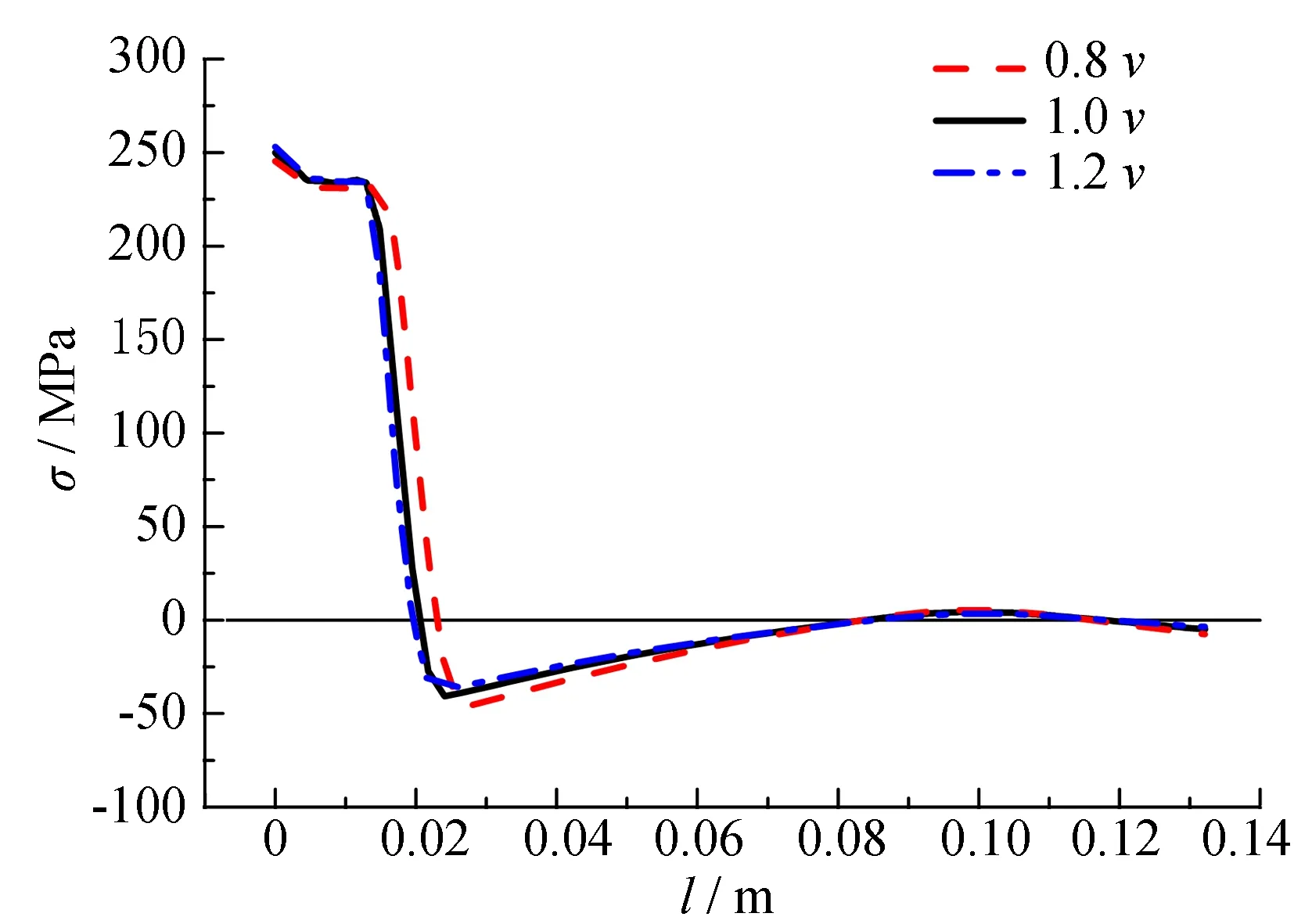
(b) U肋残余应力分布

不同焊接速度下的母板和U肋残余应力合力如图13、 14所示， 从图13、 14中可以看出， 随着混合钢U肋加劲板焊接速度的增大， 母板残余拉应力的合力和残余压应力的合力随之明显减小， U肋残余拉应力的合力和残余压应力的合力略微减小. 从分配比例来看， 母板残余拉应力和残余压应力的合力比例减小， 而U肋上的残余拉应力和残余压应力的合力比例增大.

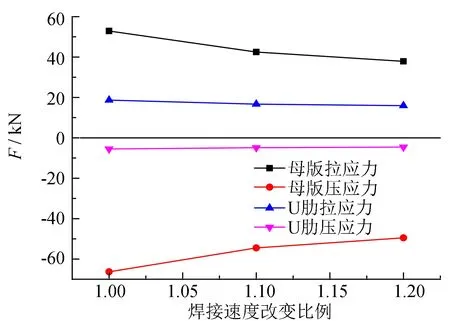
图13 不同焊接速度下的残余应力合力

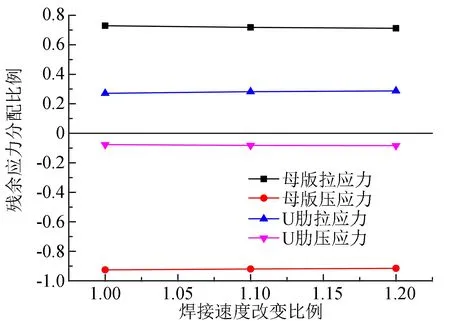
图14 不同焊接速度下的残余应力合力分配比例变化

3 结语

1) 在对混合钢U肋加劲板焊接残余应力影响因素分析中， 焊接有效功率对U肋加劲板的残余应力分布的影响最大， 其次分别为熔池面积及焊接速度的影响， 散热系数对混合钢U肋加劲板的残余应力分布影响最小.

2) 随着焊接有效功率值的增大， 母板和U肋的残余拉应力和残余压应力的数值大小均有所增大， 残余拉应力分布宽度也相应增大； 母板和U肋残余拉应力和压应力的合力均随之增大， 母板残余拉应力和压应力的合力分配比例随之增大， 而U肋残余拉应力和压应力的合力分配比例随之减小.

3) 随着熔池面积的逐步增大， 母板和U肋的残余拉应力和残余压应力的数值大小均有所增大， 残余拉应力分布宽度也相应增大； 母板残余拉应力和压应力的合力及相应的分配比例均随之增大， 而U肋残余拉应力和压应力的合力及相应的分配比例均随之减小.

4) 随着焊接移动速度的逐步增大， 母板和U肋的残余拉应力和残余压应力的数值大小均有所减小， 残余拉应力分布宽度也相应减小； 母板和U肋的残余拉应力和压应力的合力随之减小， 母板残余拉应力和压应力的合力分配比例随之减小， 而U肋残余拉应力和压应力的合力分配比例随之增大.

[1] 邓德安, 梁伟, 罗宇等. 采用热弹塑性有限元方法预测低碳钢钢管焊接变形[J]. 焊接学报, 2006, 27(1): 76-80.

[2] Withers P J, Bhadeshia H. Residual stress part-1-measurement techniques[J]. Materials Science and Technology, 2001(17): 355-365.

[3] Ma C H, Huang J H, Chen H. Residual stress measurement in textured thin film by grazing-incidence X-ray diffracation [J]. Thin Solid Films, 2002, 418(2): 73-78.

[4] 刘小渝. 磁测法测试钢结构桥梁的焊接残余应力[J]. 重庆交通大学学报, 2010, 29(1): 38-41.

[5] 陈巨兵, 周伯明, Giensu F. 应用光栅应变花和云纹干涉技术测试残余应力[J]. 中国激光, 2001, 28(8): 746-748.

[6] 班慧勇, 施刚, 石永久, 等. 超高强度钢材焊接截面残余应力分布研究[J]. 工程力学, 2008, 25(s2): 57-61.

[7] 原园, 徐颖强, 吕国志, 等. 齿轮啮合过程中安定状态残余应力的数值方法研究[J]. 工程力学, 2008, 25(10): 207-211.

[8] 张壮南, 赵亚楠, 胡磊. 基于 ANSYS 的单轴对称焊接工字形截面残余应力分析[J]. 工程力学, 2013, 30(s): 294-297.

[9] Martinson P, Daneshpour S, Kocak M,etal. Residual stress analysis of laser spot welding of steel sheets[J]. Materials and Design， 2009, 30(2): 359-366.

[10] 赵秋, 吴冲. U肋加劲板焊接残余应力数值模拟分析[J]. 工程力学, 2012, 29(8): 262-268.

(编辑： 蒋培玉)

Numerical analysis of welding residual stress of U-rib stiffened plate

ZHAO Qiu, GUO Zhiyong, YUAN Huihui, CHEN Meizhong

(College of Civil Engineering， Fuzhou University， Fuzhou， Fujian 350116， China)

A 3D thermo-elastoplastic FEM model was estabilished to simulate welding temperature field and stress field of hybrid U-rib stiffened plate. The vailidity of proposed numerical simulation method was verified by residual stress test using blind-hole method. By applying the vailated welding residual stress simulation, the effects of heat release coefficient, welding effective power, weld pool area, and welding speed, a total of 4 welding parameters, on welding residual stress distribution of hybrid steel U-rib stiffened plate were studied. The results showed that the welding effective power has the greatest influence on residual stress distribution of U-rib stiffened plate, followed by the weld pool area and welding speed, and heat release coefficient has little effect; the value of residual tensile stress and residual compressive stress of motherboard and U-rib, the distribution width of residual tensile stress, and the residual tensile stress and residual compressive stress resultants of motherboard were proportional to welding effective power and weld pool area, but inversely proportional to welding speed; however, the residual tensile stress and compressive stress resultants of U-rib were proportional to welding effective power, and inversely proportional to weld pool area and welding speed.

steel bridge; welding residual stress; thermo-elastoplastic； FEM simulation; hybrid U-rib stiffened plate

2014-05-22

赵秋(1976-)， 副教授， 工学博士， 主要从事桥梁工程研究, zhaoqiu@fzu.edu.cn

国家自然科学基金项目(51478120; 51108087)

10.7631/issn.1000-2243.2015.06.0815

1000-2243(2015)06-0815-06

TU318； U442

A