一种基于MCB的自适应和声搜索定位算法*
2015-05-11孙子文
孙 崇, 孙子文
(江南大学 物联网工程学院,江苏 无锡 214122)
一种基于MCB的自适应和声搜索定位算法*
孙 崇, 孙子文
(江南大学 物联网工程学院,江苏 无锡 214122)
针对无线传感器网络锚节点稀疏条件下节点定位中存在的翻转现象和定位精度问题,提出了一种基于MCB的自适应和声搜索定位算法。通过引入MCB算法中的采样思想,随机产生网络拓扑约束下的未知节点的坐标,引入自适应的和声保留概率和音调调节概率,达到提高搜索能力和定位精度目的。仿真结果表明:算法能有效解决翻转现象,提高定位精度,提出的算法在定位精度和计算量方面优于对比算法。
无线传感器网络; 定位; 翻转现象; 自适应; 和声搜索算法
0 引 言
由于节点能量的限制,在无线传感器网络(wireless sensor networks,WSNs)定位中,传感器节点都安装GPS装置是不现实的,且GPS一般不适合室内环境,因此,只有少量的传感器节点安装了GPS装置或已知其位置信息,其他大量的传感器节点则需要根据已知位置的节点与它们之间的距离信息获得自身的位置信息。无线传感器网络定位方法中,基于测距(range-based)技术的有接收信号强度指示(received signal strength indication,RSSI)、到达时间(time of arrival,TOA)、到达角度(angle of arrival,AOA)或不同信号的到达时间差(time difference of arrival,TDOA)等[1]。而基于测距的无线传感器网络定位常常会出现翻转现象[2,3],当节点密度低时,翻转现象尤其突出,从而造成较大的定位误差。
为了解决翻转问题,最近两阶段基于模拟退火的定位(simulated annealing-based localization,SAL)算法[2]和混合和声搜索定位算法(harmony search-based localization,HSL)算法[4]被提出。SAL算法在第一阶段获得初始估计节点位置,在第二阶段解决定位中的翻转现象和获得节点最终估计位置。HSL算法直接一阶段获得节点估计位置,并解决定位中的翻转现象。但节点定位仍存在定位误差,尤其锚节点分布不均匀、通信范围较小时,节点定位存在较大的定位误差。
本文采用基于MCB(Monte Carlo localization boxed)的自适应和声搜索定位算法解决上述问题。该算法直接一阶段定位节点位置,通过节点的拓扑约束,解决翻转现象。通过引入MCB算法中的采样思想,随机产生网络拓扑约束下的未知节点的坐标,引入自适应的和声保留概率和音调调节概率,从而提高搜索能力和定位精度。
1 定位问题描述
1.1 无线传感器网络中的翻转现象
无线传感器网络节点定位中,当节点密度较低时会导致翻转现象,翻转现象如图1所示。图1中,节点B,C,D和E是节点A的邻居节点,且节点B,C,D和E几乎是共线的,节点A的估计位置翻转到A′的位置,变成节点F的邻居节点。
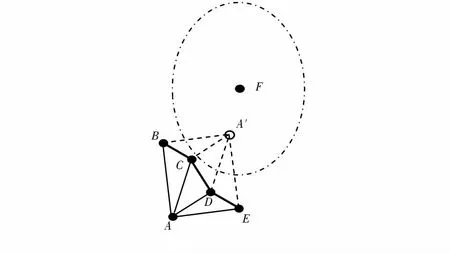
图1 翻转现象
由于翻转现象导致节点无法精确定位,造成较大的定位误差。
1.2 适应度函数定义
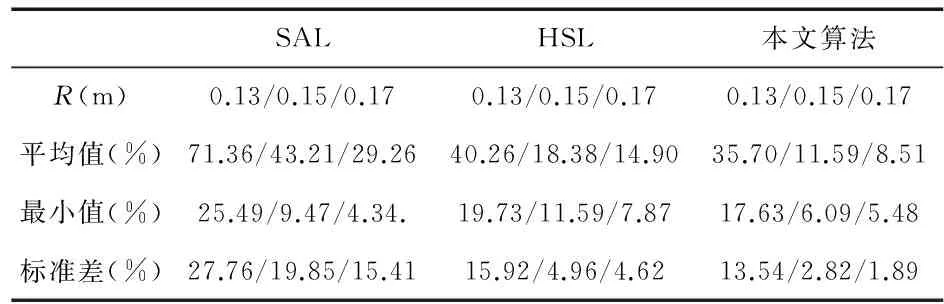
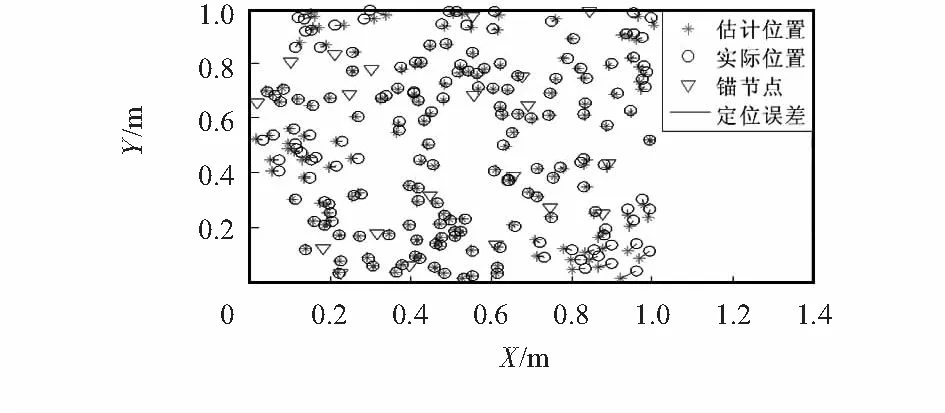
假设n个节点,包括m(m dij=rij+eij, (1) Ni={j∈1,…,n,j≠i:rij≤R}, (2) (3) (4) (5) 2.1MCB待定位节点初始化产生机制 采用MCB[6]算法中构建锚盒和滤波的采样思想,产生待定位节点的初始化坐标。采用待定位节点的一跳、两跳和三跳邻居锚节点以及部署区域T的信息进行构建锚盒,待定位节点i的锚盒表达式如式(6) Boxi= (6) (7) 式中 (xj,yj)为待定位节点i的Oi中邻居锚节点j的坐标,t为Oi中节点的总数;lij取值R,2R或3R,分别对应待定位节点i的一跳、两跳、三跳邻居节点(xj,yj)。 采用锚盒和滤波产生待定位节点初始坐标的过程,称为采样过程。待定位节点i的滤波条件[5~7]如式(8)所示 (8) 如果在锚盒内随机产生的节点坐标满足滤波条件,则采样结束且产生的节点坐标就是待定位节点的初始坐标;否则,重新采样。 2.2 自适应和声搜索优化定位算法 2.2.1 标准和声搜索算法 受音乐创作过程的启发,Geem Z W等人[8~10]提出的一种启发式全局搜索算法—和声搜索算法。乐师们凭借记忆或记录通过反复调整各乐器的音调,最终获得一个优美的和声。优化问题中的每个变量相当于每个乐器的音调,解向量对应于和声,目标函数全局最优即优美动听的音乐。 和声搜索算法可分为5个步骤[10,11]: 1)设定和声搜索算法的基本参数:变量(音调)的个数D;各变量(音调)的取值范围;解向量(和声)记忆库的大小HMS;解向量(和声)保留概率HMCR;变量(音调)调节概率PAR;最大迭代次数NI。 2)初始化解向量(和声)记忆库HM。 3)产生新解:每次根据HMCR,PAR和随机选择3个规则产生新解。 4)更新和声记忆库HM:若新解优于记忆库中最差解,则新解替换最差解,获得新的和声记忆库。 5)判断是否满足终止条件,若不满足,重复步骤(3),(4);否则,终止迭代,输出最优解。 2.2.2 和声保留概率和音调调节概率 进化算法在进化前期处于随机搜索阶段,难以得到有益的结果[11],但在随机搜索阶段种群的分布宽广是否充足对后续进化结果的优劣有重要影响。 一般而言,在前期种群分布越宽广后续进化结果越好。因此,和声保留概率HMCR由小到大变化[12],在优化的前期,较小值有利于加强全局搜索能力,在和声记忆库外进行搜索,拓宽种群的分布,减少后期陷入局部最优,后期的较大值有利于对和声记忆库进行充分搜索,找到最优解。基于锚盒大小与部署区域大小的新的和声保留概率HMCR为 HMCRi=HMCRmax-αgn·Ai/S, (9) 式中HMCRmax为和声保留概率的最大值,α为常数,满足α∈[0,1],gn为当前迭代次数,S为部署区域面积,T=[0,1]×[0,1]⊂Z2时,S=1。Ai为待定位节点i的锚盒面积,Ai的表达式如式(10)所示 (10) 音调调节概率PAR的调节由小到大[13,14],在优化的前期,较小值有利于进行全局搜索,后期的较大值有利于加强局部搜索能力,增加解的多样性,避免陷入局部最优。音调调节概率PAR[13,14]公式如式(11) PAR=PARmin+(PARmax-PARmin)gn/NI, (11) 式中PARmin,PARmax分别为音调调节概率的最小值和最大值,gn为当前迭代次数,NI为最大迭代次数。 2.2.3 自适应和声搜索定位算法描述 算法的具体实现步骤如下: 1)初始化基本参数与和声记忆库HM 通过MCB待定位节点产生机制产生HMS个解,加入解向量(和声)记忆库。 2)产生新解 a.节点i的坐标根据HMCRi在和声记忆库随机选择HMS个解中一个节点i的坐标或在变量取值范围内通过MCB待定位节点产生机制产生。 b.当节点i的坐标在和声记忆库随机选择产生时,根据PAR对节点i的坐标进行局部扰动。 3)更新和声记忆库HM 若新解优于记忆库中最差解,则新解替换最差解,获得新的和声记忆库。 4)判断是否满足终止条件,若不满足,重复步骤(2)、步骤(3);否则,终止迭代,输出最优解。 3.1 仿真与参数设置 SAL算法中的参数设置[5,8]为:初始温度T0=0.1,终止温度Tf=10-11,扰动次数P=10,Markov链长度系数Q=2,冷却因子α=0.8,收缩因子β=0.94。HSL算法中的参数设置[4]为:和声记忆库的大小HMS=50,最大迭代次数I=2000,和声保留概率HMCR=90 %,音调调节概率PAR=1 %,随机选择概率PSR=1 %。本文算法中的参数设置为:和声记忆库的大小HMS=50,最大和声保留概率HMCRmax=99.44 %,最大音调调节概率PARmax=99.44 %,最小音调调节概率PARmin=0.56 %,最大迭代次数NI=105。 3.2 仿真结果与分析 为了评价算法的定位性能,采用标准定位误差(NLE),公式如式(12) (12) 1)定位精确度 表1 定位算法性能指标 表1所示仿真结果为通信半径R分别为0.13,0.15,0.17 m时不同场景下, SAL算法、HSL算法和本文算法均通过20次仿真结果的标准定位误差值的平均值、最小值和标准差。在所有仿真场景中,从参数设置中可知,本文算法的适应度函数计算次数为NI=105,HSL算法的适应度函数计算次数[4]为105,SAL算法的平均适应度函数计算次数[5,8]为7.1×105。从表1可以看出:本文算法标准定位误差值的平均值比SAL算法和HSL算法更小,本文算法标准定位误差值的标准差同样比SAL算法和HSL算法更小,即本文算法定位精度一致性较好,与适应度函数计算次数相同的HSL算法比,本文算法标准定位误差值的最小值方面均优于HSL算法,与适应度函数计算次数较大的SAL算法比,通信半径较小时,本文算法在标准定位误差值的最小值方面优于SAL算法。本文算法总体上提高了定位精度。 2)翻转现象 图2是本文算法在通信半径R=0.15 m时的定位效果图,图3是SAL算法同样在通信半径R=0.15 m时第一阶段的定位效果图,从2图和图3对比中可以看出:SAL算法在R=0.15 m时第一阶段节点定位存在较多翻转现象,如图3中右下角的一些节点,且由于节点的翻转导致其他节点无法精确定位。本文算法在R=0.15 m时有效解决了定位的翻转现象,实现节点精确定位。 图2 本文算法在R=0.15 m时定位效果 图3 SAL算法在R=0.15 m时第一阶段定位效果 本文提出了一种基于MCB的自适应和声搜索定位算法,该算法能够有效地解决无线传感器网络锚节点稀疏的节点定位问题,解决翻转现象。仿真结果表明:本文算法能够提高定位精度和定位精度一致性,该算法在定位精度和计算量方面优于SAL与HSL算法。 [1] 孙子文,王鑫雨,白 勇,等.基于信度和早熟检验的混沌粒子群优化定位算法[J].传感器与微系统,2013,32(9):129-133. [2] Kannan A A,Mao G,Vucetic B.Simulated annealing-based wireless sensor networks localization with flip ambiguity mitigation[C]∥IEEE Vehicular Technology Conference(VTC),Melbourne:IEEE,2006:1022-1026. [3] Kannan A A,Fidan B,Mao G.Analysis of flip ambiguities for robust sensor network localization[J].IEEE Trans Veh Technol,2010,59(4):2057-2070. [4] Manjarres D,Del Ser J,Gil-Lopez S,et al.On the application of a hybrid harmony search algorithm to node localization in anchor-based wireless sensor networks[C]∥Intelligent Systems Design and Applications (ISDA),Cordoba:IEEE,2011:1014-1019. [5] Baggio A,Langendon K.Monte Carlo localization for mobile wireless sensor networks[J].Ad Hoc Networks,2008,6(5):718-733. [6] Hu L X,Evans D.Localization for mobile sensor networks[C]∥ACM MobiCom’04,Philadelphia:ACM SIGMobile,2004:45-57. [7] Vecchio M,López-Valcarce R,Marcelloni F.A two-objective evolutionary approach based on topological constraints for node loca-lization in wireless sensor networks[J].Applied Soft Computing,2012,12(7):1891-1901. [8] Geem Z W,Kim J H,Loganathan G V.A new heuristic optimization algorithm:Harmony search[J].Simulation,2001,76(2):60-68. [9] Geem Z W.Music-inspired harmony search algorithm:Theory and applications[M].Berlin:Springer,2009. [10] 雍龙泉.和声搜索算法研究进展[J].计算机系统应用,2011,20(7):244-248. [11] 乔 英,高岳林,江巧永.改进的多目标和声搜索算法[J].计算机工程,2012,38(18):144-146. [12] Xiang W I,An M Q,Li Y Z,et al.An improved global-best harmony search algorithm for faster optimization[J].Expert Systems with Applications,2014,41(13):5788-5803. [13] Mahdavi M,Fesanghary M,Damangir E.An improved harmony search algorithm for solving optimization problems[J].Applied Mathematics and Computation,2007,188(2):1567-1579. [14] 刘思远,柳景青.一种新的多目标改进和声搜索优化算法[J].计算机工程,2010,46(34):27-30. A self-adaptive harmony search localization algorithm based on MCB* SUN Chong, SUN Zi-wen (School of Internet of Things Engineering,Jiangnan University,Wuxi 214122,China) Aiming at problem of flip ambiguity and localization precision,a self-adaptive harmony search algorithm for wireless sensor networks(WSNs) node localization is proposed.Based on the Sampling Theory of Monte Carlo localization boxed (MCB),the coordinates of unknown nodes are generated randomly under the restriction of the network topology constraints,in order to improve the search ability and the localization precision,introduce adaptive harmony memory considering rate (HMCR) and pitch adjusting rate (PAR).Simulation results show that the algorithm can effectively address the flip ambiguity and improve the localization precision,and the algorithm outperforms,in terms of localization precision and computational complexity compared with otherst. wireless sensor networks(WSNs); localization; flip ambiguity; self-adaptive; harmony search algorithm 2015—01—22 国家自然科学基金资助项目(61174032);江苏省自然科学基金面上项目(BK20131107) 10.13873/J.1000—9787(2015)04—0119—04 TP 393 A 1000—9787(2015)04—0119—04 孙 崇(1990-),男,江苏泗阳人,硕士研究生,研究方向为无线传感器网络。

2 自适应和声搜索定位模型
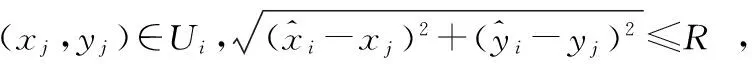
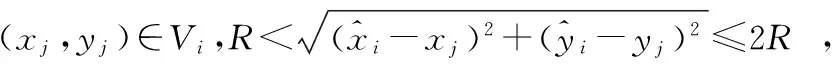
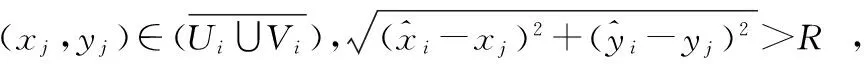
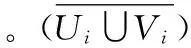
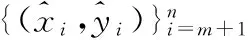
3 仿真与分析
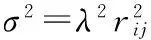

4 结束语
