加筋土边坡非线性优化设计方法研究

王家磊

(中铁第四勘察设计院集团有限公司， 湖北 武汉 430063)



加筋土边坡非线性优化设计方法研究

王家磊

(中铁第四勘察设计院集团有限公司， 湖北 武汉 430063)

提出了一种优化设计加筋土边坡的方法。首先利用极限平衡法确定多组加筋土边坡设计参数与其稳定性系数的映射关系，再将设计参数和所求出的安全系数做为输入、输出样本采用遗传算法进化BP神经网络训练网络模型，然后建立以上述设计参数为自变量的加筋土边坡造价的目标函数，神经网络预测出的稳定性系数大于某个值为约束条件的优化设计模型。在此基础上开发了MATLAB环境下的加筋土边坡优化设计系统，编制了遗传算法，粒子群算法和复合形法的计算求解程序。以某加筋土边坡为工程实例，得到了安全、经济的设计参数取值和对应的造价。

加筋土边坡； 优化设计； TGLSS； GABP神经网络； 算法程序； 最优参数

现代加筋土技术因解决了岩土工程中许多技术难题，得以蓬勃发展[1]。加筋土结构已被实际工程证明具有耐久、可靠、造价低、抗地震和动荷等特点，据国内部分工程资料统计，加筋土边坡的造价一般为挡土墙的40%～60%。加筋土结构在边坡工程安全和经济上具有极大的优势。

加筋土边坡的优化设计，许多岩土工作者做了大量工作。黄蜂[2]讨论了加筋土边坡设计中主要设计参数对边坡稳定性的影响，以边坡造价为目标函数，采用Monte-Carlo抽样方法得出最优化参数。王建[3]等对汶川地震震区路堤震害进行调查，提出了路基中上部铺设短筋的优化设计方法，并利用有限差分动力强度折减法分别对常规加筋模型和优化模型进行了抗震性能计算，证明了优化模型的有效性。涂帆[4]等以筋材总长度最小为控制目标，不发生任何模式破坏为约束条件，建立非线性约束规划的优化设计数学模型并求解。Uchihata, Kenzo[5]，胡新丽[6]，Donvan.T.A.[7]等也对加筋挡土墙、边坡优化设计进行了研究。但由于加筋技术引入的时间还不长，同时以往的优化设计都是以稳定性为主要目标，忽略了经济性因素。

本文在前人所做研究基础上，以某加筋土边坡工程项目为依托，选取影响边坡稳定的三大主要设计参数：加筋长度、加筋间距和坡比，且在各自取值范围内选取100组不同设计参数，采用边坡稳定性计算软件TGLSS将每组设计参数与其稳定性系数一一对应。在此基础上将设计参数和所对应的安全系数做为输入、输出样本，采用遗传算法进化BP神经网络训练网络模型，然后建立加筋土边坡造价的目标函数，以网络模型预测出的安全系数大于某个值为约束条件，分别采用混合遗传算法、自适应粒子群算法和复合形法求解优化模型。

1 加筋土边坡优化设计模型

1.1 设计参数与稳定性系数的映射

首先，根据加筋土边坡实际工程情况选取影响边坡安全性的重要设计参数，文献[2]利用正交试验理论对影响加筋土边坡稳定性的因素进行显著性分析，得出了坡比B、加筋长度L以及加筋间距D的取值范围为：1∶1.5≤B≤1∶0.5、H≤L≤1.5H以及0.2 m≤D≤2.5 m。上述参数能很好地反应加筋土边坡的造价，也易求出特定地质条件下的稳定性系数。故本文选用上述三参数作为自变量进行研究。

根据选取的设计参数，在其取值范围内随机多组赋值，采用TGLSS极限平衡法边坡稳定性计算软件求出每组设计参数对应的稳定性系数，将得到的多组设计参数与稳定性系数对应关系作为人工神经网络的输入、输出样本训练网络。图1为等坡高单级坡高为H=8 m，加筋长度L=23 m，加筋间距D=0.8 m，坡比B=1时的计算结果，得出Fs=1.664。

图1 TGLSS软件计算边坡稳定性系数示意图

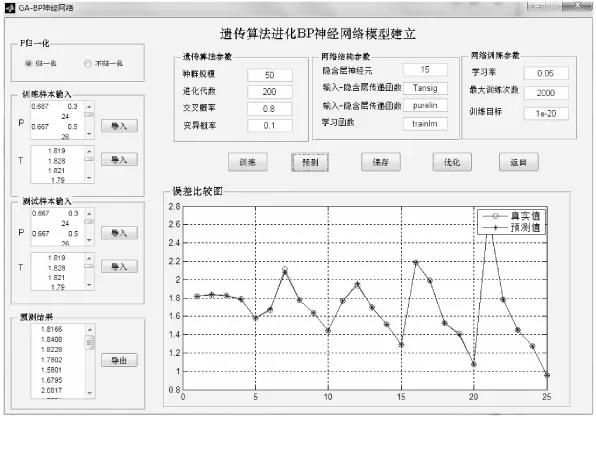
图2 GABP神经网络模型界面示意图

最后，根据以上得到的人工神经网络模型建立起映射关系后，对于任意一组设计参数，均可利用该模型预测相应的边坡稳定性系数。

1.2 GABP神经网络

人工神经网络(ANN)方法是在生物技术的基础上借鉴人脑的结构和工作原理而形成的一种动态信息处理系统，具有很强的非线性动态处理能力。利用ANN的工作原理，可以建立影响边坡稳定性的设计参数与稳定性系数的非线性映射模型，从而用来预测和评价边坡的安全性[8]。该理论已广泛应用于岩土工程界，并解决了大量的工程问题，其中以BP神经网络模型应用最多，也较为成熟[9-10]。但BP神经网络存在收敛速度慢和容易陷入局部极优的缺点，本文采用神经网络预测模型作为约束条件，对模型的预测精度和网络的收敛能力提出了更高的要求。

理论分析和实验结果表明，遗传算法作为一种新型的全局优化搜索算法，将它用于神经网络权值的训练学习能得到较好的结果，它能克服BP算法中学习效率底、收敛速度慢、容易陷入局部最优化等缺点[11,12]。本文将遗传算法和BP神经网络相结合，用GA来优化BP神经网络的权值和阈值。将所有构建的神经网络的权值作为一组染色体，也就是染色体的维数为权值的个数，采用实数编码，隐节点和输入层的变化函数均采用Sigmoid函数，神经网络的误差计算作为适应度函数，避免了函数求解梯度的问题，进而能相应提高计算速度和避免陷入局部极小。图2为笔者自行编写的遗传算法进化BP神经网络(GABP)的界面程序，网络包含2个隐含层次，支持excel文档的导入和数据输入，是整个加筋土优化设计系统的网络训练和预测部分，同时还提供网络模型保存功能，后期的优化设计计算直接调用已有网络模型。

由预测结果及误差比较(图2)，预测效果良好。

1.3 优化设计计算模型

设计的一般思想是在保证工程安全的前提下，以造价最低为目标。将待解决的问题具体化，就是建立一个将设计参数作为自变量，用设计参数表示加筋土边坡造价为目标函数，以对应的设计参数预测出的边坡的稳定性为约束条件的优化设计模型，然后寻求目标函数的最小值(造价最小值)。根据以上分析可建立如下模型：

式中：f(x,c)为加筋土边坡的造价函数(以每延米造价为目标函数)；x为设计参数向量；c为材料单价向量，如加筋单价，填土单价等；lb，ub分别为设计参数的上下限；gu(x) 为神经网络预测稳定性系数的函数；Fs为稳定性系数。

1.4 求解优化设计模型算法实现

由于上述约束条件的非连续性和非常规性，MATLAB非线性优化设计工具箱以及系统自带的遗传算法优化计算函数就失去了作用。为了避免非线性最优化需要求梯度问题存在的困难，故采用混合遗传算法、自适应粒子群算法和随机向量法中的复合形法求解，多种计算方法既可以对比计算结果，亦能判断结果是否为局部极小值。

图3和图4分别显示了遗传算法和粒子群算法的计算编程流程，图5为复合形法计算流程图。

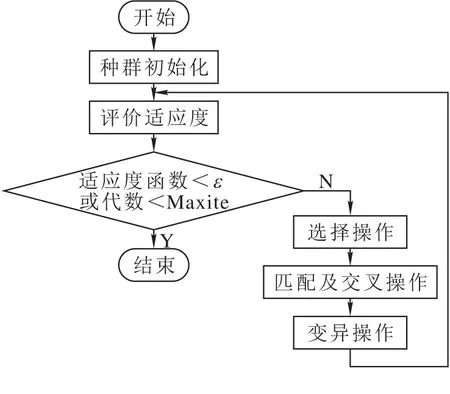
图3 遗传算法计算流程图

图4 粒子群算法计算流程图

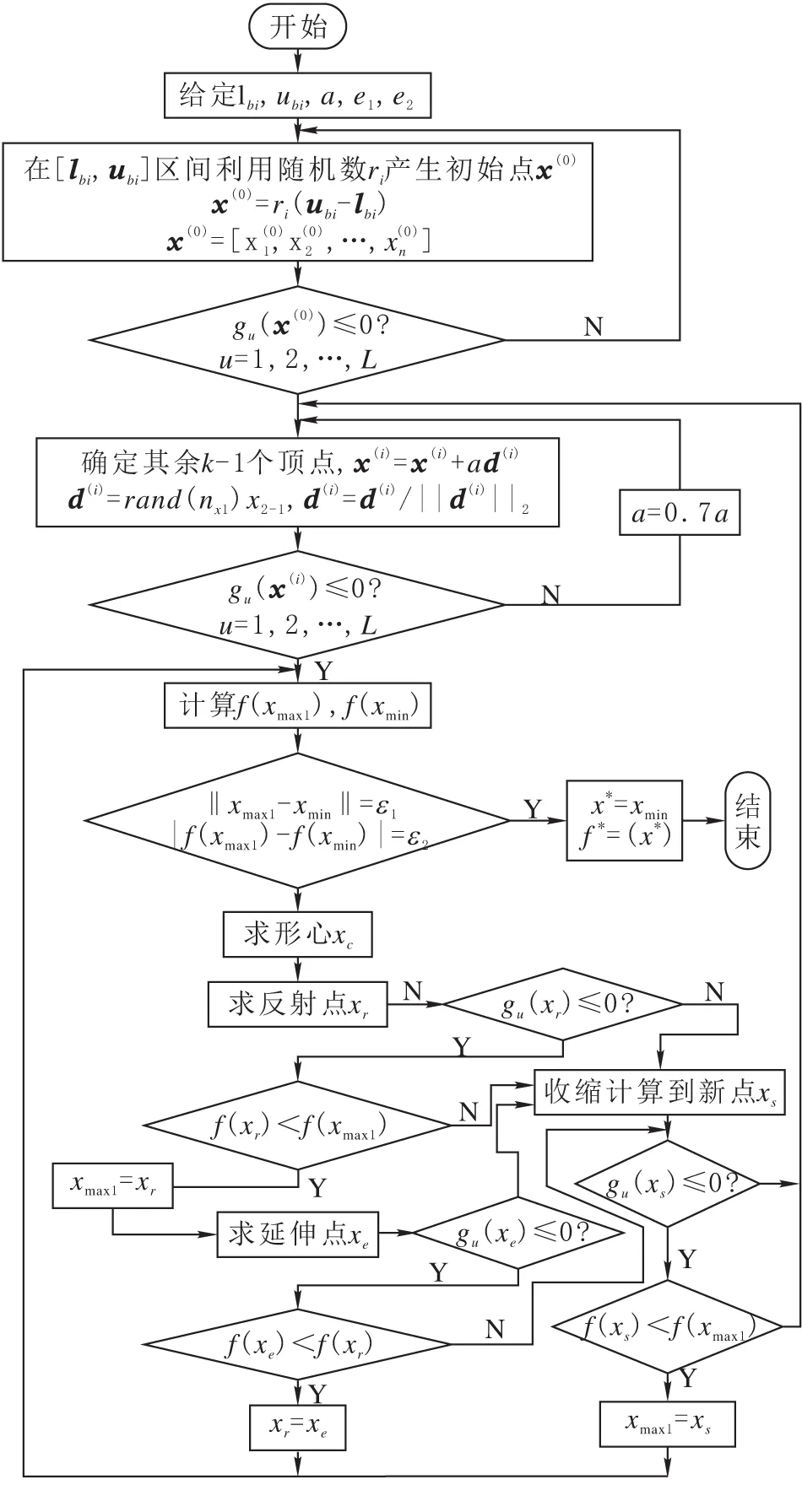
图5 复合形法计算流程图

分别依照算法流程图编制计算程序界面，界面能直接调用已经训练和保存好的神经网络模型作为约束条件进行计算。

对于有约束条件的遗传算法和粒子群算法，利用内点罚函数法构造罚函数，即可将有约束极小化问题转化为无约束极小化问题。罚函数

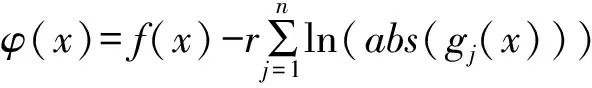
2 工程实例

拟建工程位于市区，场区大部分为填方边坡工程，其中最大坡高约27.5 m，边坡总长约581 m，设计采用单向塑料土工格栅加筋填筑。填方边坡位于站址西侧、南侧及东侧冲沟低洼处，坡顶标高即为站址初平标高，坡底标高16.18～40.01 m，坡高约3～27 m。超载20 kPa, 为外部进场公路。

根据《岩土工程勘测报告》，具体加筋土边坡物理参数见表1。

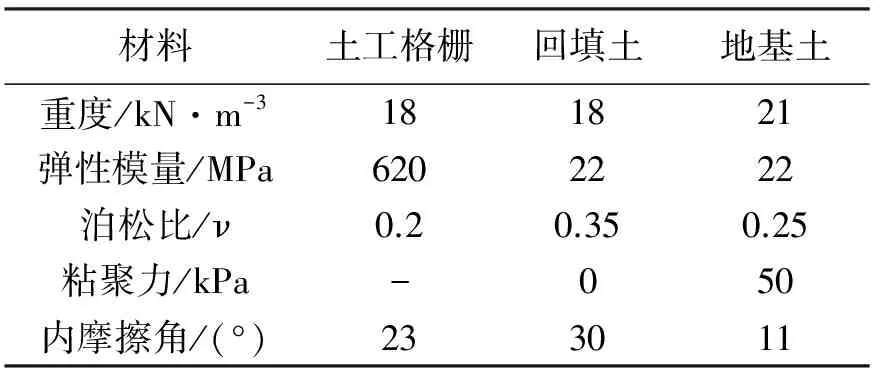
表1 加筋土边坡有关计算参数

本文对K0+771.00-K0+811.00桩号H=24 m高边坡进行优化设计。按规范SL/T225-98将边坡分为等高三级，为了计算方便，假定加筋间距均匀分布，不考虑底部格栅距离坡底高度造成的筋材过密引起的造价增加。采用不同设计参数计算边坡稳定性系数，得到100组样本训练GA-BP神经网络模型。表2给出其中的25组设计参数和稳定性系数的映射关系。

以每延米加筋土边坡的造价建立目标函数，设置最小稳定性系数Fs=1.3，得出模型为

s.t 24≤x1≤31

0.3≤x2≤1.5

0.667≤x3≤2

φ(GABP)-1.3>0

式中：h为单级坡高，取8 m；c1、c2分别为加筋单价和填土单价，分别取30和9.49元/m2；x1为加筋长度；x2为加筋间距；x3为综合坡比；φ(GABP)为神经网络输出函数。

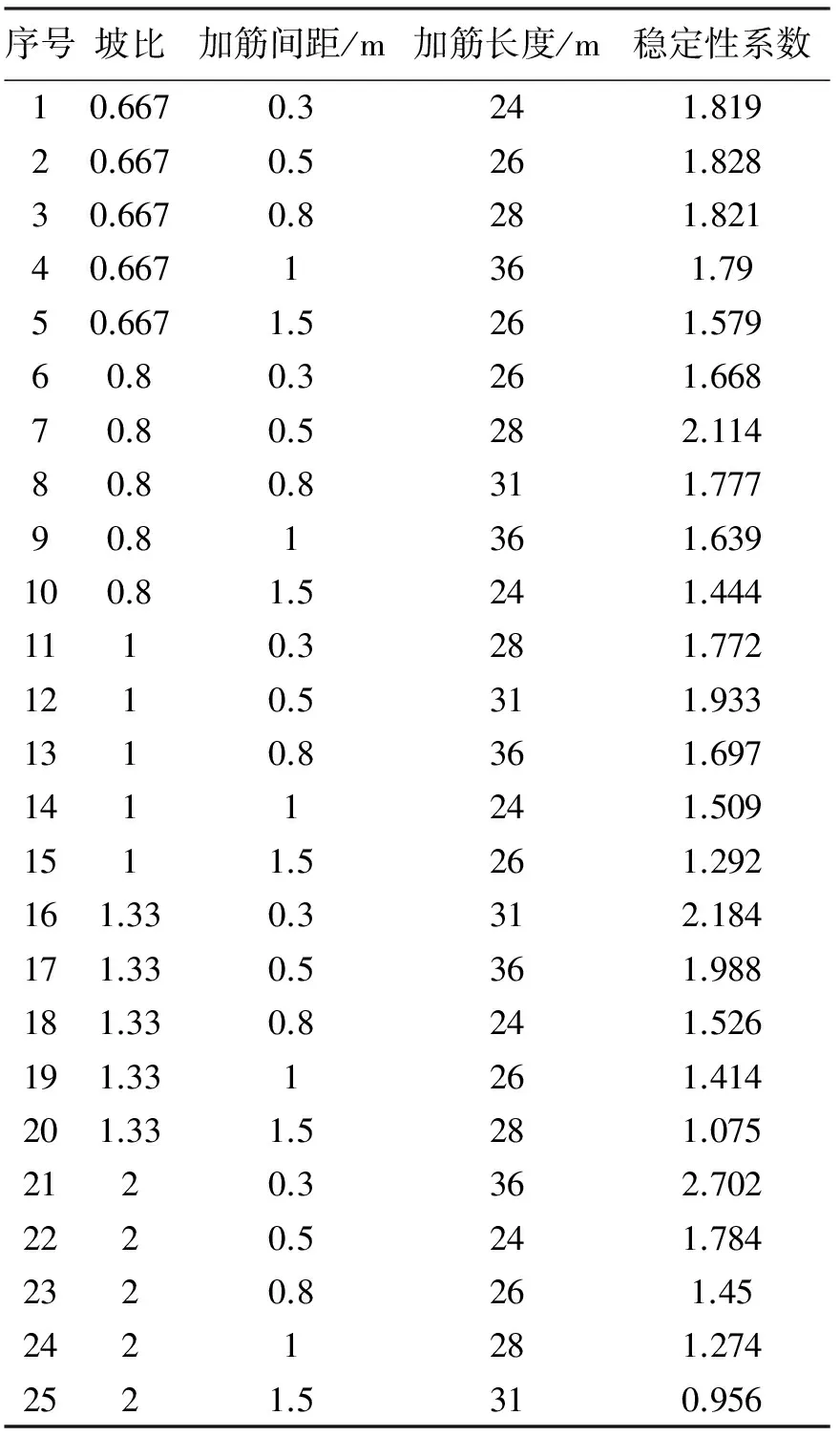
表2 设计参数与稳定性系数映射

分别采用3种方法计算，遗传算法选取种群数为500，进化代数为300；粒子群算法粒子数为300，迭代次数为200；复合形法以误差为1exp-12为迭代终止条件。计算结果如图6、7、8所示。表3为计算结果统计图。分析图表可知，三种算法都达到了全局最优解。由迭代次数与造价曲线图可知，遗传算法和粒子群算法逐渐趋近最优解，而复合形法存在发射、延伸、收缩的实效而产生起伏，但最终还是趋近了满足精度条件的最优解。且三种计算方法得出的结果差别不大。

图6 遗传算法计算结果

图8 复合形法计算结果

选择设计参数加筋长度为24 m，加筋间距为1.1 m，坡比为1.4，造价为3.014万元/m2，计算稳定性系数为1.324。

表3 最优参数和造价对照

计算结果表明，GABP神经网络能很好地映射加筋土边坡设计参数与稳定性系数之间复杂的非线性关系，智能算法和非线性直接解法能很好地解决这种非常规的约束条件。

4 结论

影响加筋土边坡设计的因素很多，本文选取了三个重要设计参数，针对某一具体边坡进行研究，首先建立设计参数与稳定性系数的映射关系，然后利用神经网络来反演稳定性系数，将其作为优化模型的约束条件，以设计参数构造目标函数，再利用智能算法和非线性最优化直接解法求得最优参数和最小造价，实现了既经济、又安全的要求，该方法为解决工程中无法找出参数间无明显函数的非线性复杂问题提出了一种思路。

基于该方法开发的加筋土边坡优化设计系统能训练GABP神经网络，三种求解方式能很好地判断结果是否陷入局部解，能求出最优设计参数，具有较强的实用价值。

[1] 杨果林. 现代加筋土技术应用与研究进展[J].力学与实践, 2002, 24(01):9-17.

[2] 黄 峰. 基于强度折减有限差分的高陡加筋土边坡稳定性分析及优化设计初探[D].西安,长安大学, 2006.

[3] 王 建. 土工格栅加筋路堤抗震优化设计方法研究[J].四川大学学报, 2010, 42(05):99-1103.

[4] 涂 帆. 加筋土挡墙的优化设计[J].华侨大学学报(自然科学版), 2008, 29(02):276-279.

[5] Uchihata Kenzo. Design concept and some case histories of stell grid reinforced earth wa- ll[C].Proceedings of the 10thInternational Offshore and Polar Engineering Conference, 2000:386-390.

[6] 胡新丽，唐辉明，陈建平.高速公路顺层路堑边坡优化设计方法[J].中国地质大学学报, 2001, 26(04):373-376.

[7] Donovan T A. Optimum mine pit slop design[C]. Preprints Proceedings 19thU.S Symposium on Mechanics, 1978.

[8] 尹顺德, 冯夏庭, 张友良,等. 滑坡加固方案优化的并行进化神经网络方法研究[J].岩石力学与工程学报, 2004, 23(16):2698-2702.

[9] 冯夏庭. 智能岩石力学导论[M].北京,科学出版社, 2000.

[10] 陈昌彦,王思敬,沈小克.边坡稳定性的人工神经网络预测模型[J].岩土工程学报, 2001,23(02):157-161.

[11] 郭晓婷,朱 岩.基于遗传算法的神经网络[J].清华大学学报(自然科学版), 2000, 40(10):116-119.

[12] 李伟超,宋大猛,陈 斌.基于遗传算法的人工神经网络[J].计算机工程与设计, 2006, 2(27):316-318.

[责任编校： 张岩芳]

Nonlinear- Design Optimization of theReinforced Soil Slope

WANG Jialei

(ChianRailwaySiyuanSurveyandDesignInstituteGroupCo.,LTD,Wuhan430063,China)

An optimization method of the reinforced earth slope was proposed in the paper. Firstly, the Limit Equilibrium method was used to evaluate the stability of the slope, design parameters of which were specified. Secondly, the design parameters and factor of safety presented above were adopted as input and output variables respectively to the GABP-NN, then the objectivity function of cost of the design parameters was established and the constraint condition of the factor of safety that is greater than a expected value was identified. On the basis of this theory, an optimum design system of reinforced earth slope was developed based on MATAB, GA, PSO and CM was programmed to solve the optimum mode. This method has been applied in the design of reinforced soil slope of a project, and optimum design parameters and cost were obtained.

reinforced soil slope; design optimization; GABP-NN; algorithm programming; optimum parameters

2014-08-11

王家磊(1984-)， 男， 江苏泰兴人，东南大学硕士研究生，研究方向为岩土工程

1003-4684(2015)01-0106-05

U417.1

A