基于粒子群算法的储能装置控制器优化

程 鑫

(广东电网发展研究院有限责任公司， 广东 广州 510080)



基于粒子群算法的储能装置控制器优化

程 鑫

(广东电网发展研究院有限责任公司， 广东 广州 510080)

提出了一种基于粒子群算法的储能装置控制器优化方法，与传统的控制器设计方法相比，避免了复杂的数学计算。在四机两区域电力系统进行了仿真分析，确定了储能装置最佳安装位置，并以联络线功率反馈作为控制器的输入信号，分析了不同故障下储能装置的功率振荡抑制效果。通过对实际系统的仿真研究表明了该方法的有效性，且适用于大规模电力系统。

储能装置； 功率振荡； 粒子群算法； 控制器优化

电力系统受到扰动时如果缺乏足够的阻尼就会失去稳定，并发生低频振荡现象。国际大电网会议第38届研究委员会曾组织专门工作组(Task Force 38.01.07)对低频振荡进行研究，其结论指出：为消除振荡的威胁，首先应仔细考虑研究整定系统中主要发电机的电力系统稳定器(PSS)；其次应研究系统中现有高压直流输电(HVDC)、静止无功补偿器(SVC)附加控制器的参数整定，使之提供附加阻尼效果；然后考虑利用TCSC等FACTS装置提供平滑的阻尼控制；最后可考虑在系统中增加完全用于阻尼振荡的新装置[1]。

近年来，电力电子技术有了突飞猛进的发展。研究表明，储能装置不仅具有改善系统暂态稳定性的特点，其附加的阻尼控制对于抑制由扰动引起的低频振荡现象也有明显作用[2]。美国西海岸电网在上世纪80年代就曾利用超导储能装置抑制了该系统0.35 Hz的低频振荡。

利用储能装置抑制电力系统功率振荡需要采取有效的控制策略，并得到合适的控制器参数。目前，电力系统控制器设计广泛地采用线性控制理论，通过将系统在运行点线性化得到系统的状态方程，进而采用极点配置法、留数法、相位补偿法等设计控制器参数。文献[3]利用反步法设计了用超导磁储能装置抑制联络线功率振荡的控制器，文献[4-5]将模糊控制应用于储能装置以提高电力系统稳定性。

现有文献用储能装置抑制功率振荡的控制方法大多比较复杂，获取控制器参数存在一定困难。本文提出利用粒子群优化(Particle Swarm Optimization, PSO)算法优化储能装置控制器，该方法主要通过系统仿真修正控制器参数以获得较好的控制效果，可以避免复杂的数学计算，且适用于大规模电力系统。

1 粒子群算法优化控制器原理

1.1 粒子群算法原理

1995年美国的James Kennedy和Russell Eberhart提出了粒子群算法[6]。粒子群算法是一种随机搜索算法，粒子通过飞行速度决定它们的搜索方向和搜索范围，根据个体自身经验的积累和群体优秀信息的学习来调节飞行速度，在空间中搜索最优解。

粒子群算法的寻优过程可描述如下：初始化粒子群的速度和位置，在搜索空间中寻找最优解；迭代计算粒子群的个体最优解和全局最优解，并利用个体最优信息和全局最优信息来调整粒子的飞行速度和位置。粒子群第k+1次迭代公式为：

(1)

xijk+1=xijk+vijk+1

(2)

式中：xi、vi为第i个粒子的位置与速度；pi为第i个粒子的个体最优值，pg为粒子的全局最优值；w为惯性权重系数；c1、c2为加速常数，通常在0～2之间取值；r1、r2为两个取值在0～1之间的相互独立的随机数。

研究表明，惯性权重系数w是影响收敛效果的重要因素。较大的w值能提高算法的收敛速度，而较小的w值有利于提高算法的收敛精度[7]。据此提出一种非线性自适应调整的策略[8]，即

(3)

式中：wmin、wmax为惯性权重系数的最小、最大取值；kmax为最大迭代次数。

图1为a=2，3，4时惯性权重随迭代次数变化曲线。可以看出，当a=3时，在迭代初期提供较大的惯性权重，提高算法收敛速度；在迭代中期保持足够的搜索能力；在迭代后期w可以保持较小值，提高算法的收敛精度。本文在进行控制器优化的过程中即取a=3。

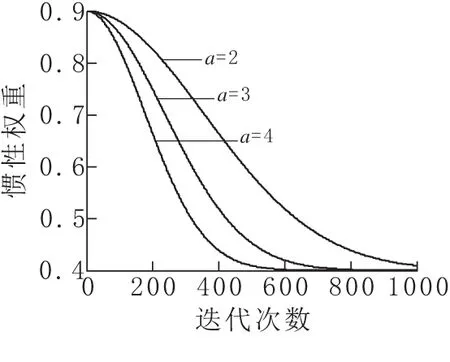
图1 惯性权重系数与迭代次数的相关曲线

1.2 目标函数

ITAE(Integraloftimemultipliedbytheabsolutevalueoferror)准则指的是时间乘以误差绝对值的积分，以ITAE准则作为性能指标的控制系统一般具有过渡平稳、反应快速等特点，可以很好地限制过渡过程后期出现的误差。结合电力系统自身的特点，本文采用发电机功角偏差的ITAE指标或者线路有功功率偏差的ITAE指标作为粒子群算法的目标函数

(4)

式中：t为系统响应时间，Δy为发电机功角偏差或线路有功功率偏差。

为抑制电力系统功率振荡，储能装置控制器的优化问题实际上可以描述为ITAE指标最小的问题，即

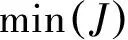
(5)

1.3 粒子群算法优化储能装置控制器流程

应用粒子群算法优化储能装置控制器的流程如图2所示，主要步骤如下：

1)设置粒子群算法的种群数以及最大迭代次数，对粒子进行随机初始化。

2)将当前的粒子值赋给储能装置控制器参数，对系统进行仿真计算。

3)根据式(4)计算各个粒子对应的目标函数值，利用式(5)确定并更新粒子的个体最优解和全局最优解。

4)根据式(1)和式(2)更新各个粒子的速度和位置，形成下一代粒子。

5)判断是否满足迭代终止条件。如果不满足，转向步骤2)；如果满足，则迭代终止，输出控制器参数及其目标函数值。

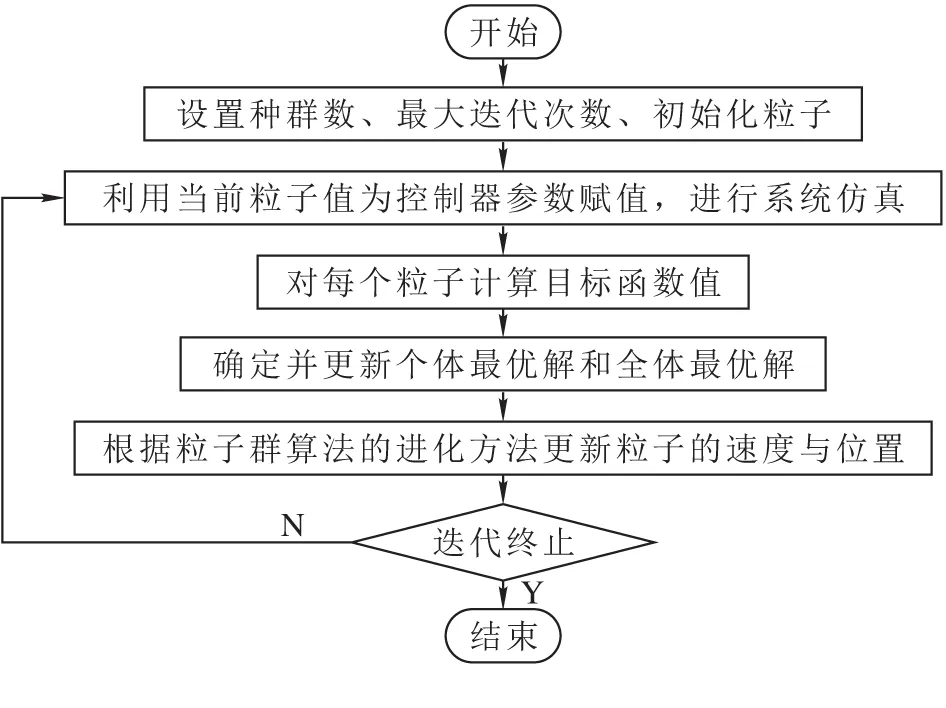
图2 粒子群算法优化储能装置控制器流程图

2 四机两区系统的仿真研究

2.1 仿真系统及控制器模型介绍

针对本文所提的控制器优化方法，采用四机两区域系统进行仿真分析。经典的四机两区域电力系统如图3所示，系统参数详见文献[9]。

图3 四机两区域系统

储能装置的功率振荡阻尼(PowerOscillationDamping，POD)控制器模型如图4所示，其本质上属于单输入、单输出超前-滞后相位补偿控制器[10]。图中，K/(1+sTr)为输入信号的放大环节，Tr为输入信号测量时间常数，可设置为0.01s；sTw/(1+sTw)为隔直环节；(1+sT1)/(1+sT2)为POD控制器的超前-滞后补偿环节，每个超前-滞后补偿环节最多可实现60°的相位补偿。实际运行过程中由于储能装置自身容量的限制，在控制器的模型中还必须考虑限幅环节，限幅值根据储能装置的容量而定。

图4 储能装置控制器结构

根据图4可将POD控制器表达成传递函数的形式：

(6)

2.2 储能装置安装位置的选择

电力系统功率振荡本质上为发电机转子间的振荡，发电机功角是反应系统功率振荡的最直接的系统状态量。选择发电机功角差Δδ13(1号发电机与3号发电机的功角差)作为储能装置POD控制器的输入信号，以研究确定储能装置在系统中的最佳安装位置。

将储能装置依次安装在各母线上，当系统发生故障时，利用粒子群算法对POD控制器进行优化，得到各母线下控制器的目标函数值，最后再对比各个目标函数值，选出储能装置的最佳安装位置。利用粒子群算法优化得到的控制器参数和目标函数值见表1。

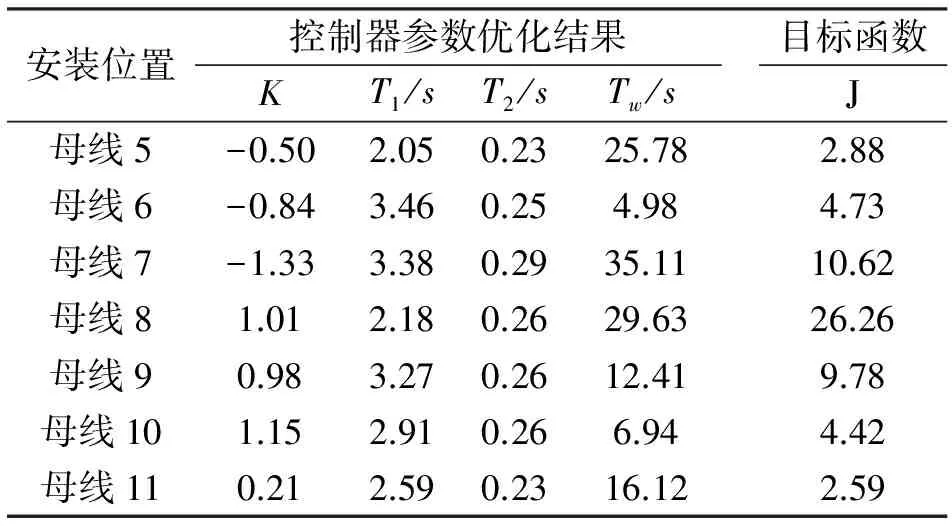
表1 各母线安装储能装置控制器优化结果

故障设置母线7在正常运行1s后发生三相瞬时性短路故障，故障持续时间0.1s。

从表1可以看出，储能装置安装在母线5或者母线11的时候，粒子群算法优化后的目标函数值较小，即其ITAE指标较优。另外，对比安装储能装置后的功角振荡波形(图5)，当储能装置安装在母线5或者母线11的时候对发电机功角振荡抑制效果较好，因此储能装置的最佳安装位置为母线5或者母线11。

2.3 联络线功率反馈优化控制

实际系统中，由于测量和通讯技术的限制，难以直接利用发电机功角差Δδ13作为储能装置控制器的输入信号。而系统的联络线功率信号中包含有系统区域间振荡模式的相关振荡信息，且其容易测量，因此考虑利用线路功率ΔP作为控制器的输入。

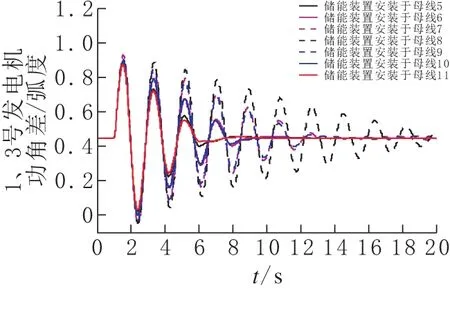
图5 储能装置安装各母线处的功角振荡抑制效果

将储能装置安装于2.2节储能装置最佳安装位置母线5(或母线11)，仍然考虑节点7在正常运行1s后发生三相瞬时性短路故障，故障持续时间0.1s。为减小区域间的功率振荡，以联络线功率ΔP78(母线7与母线8间的功率差)作为控制器输入信号，优化结果见图6。

图6 联络线功率反馈控制下的功率振荡抑制效果

为验证联络线功率反馈优化得到的控制器参数的适用性，对不同故障下联络线两端线路上的功率振荡进行仿真(图7)。(受篇幅所限，本文仅给出母线6、母线9、母线11发生短路故障时的功率振荡曲线)。

(a)母线6发生短路故障

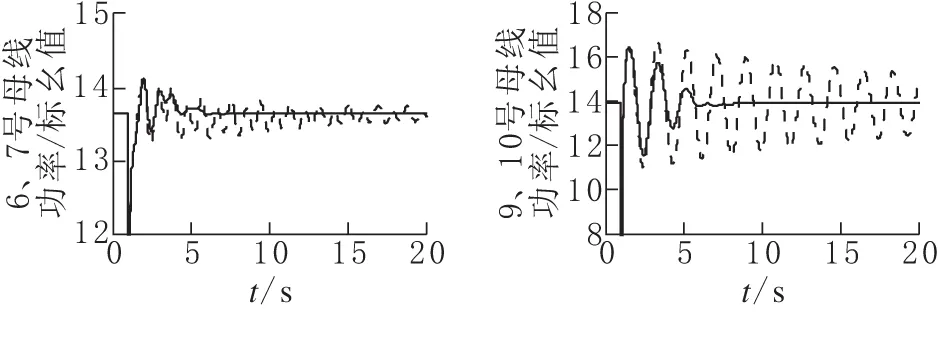
(b)母线9发生短路故障

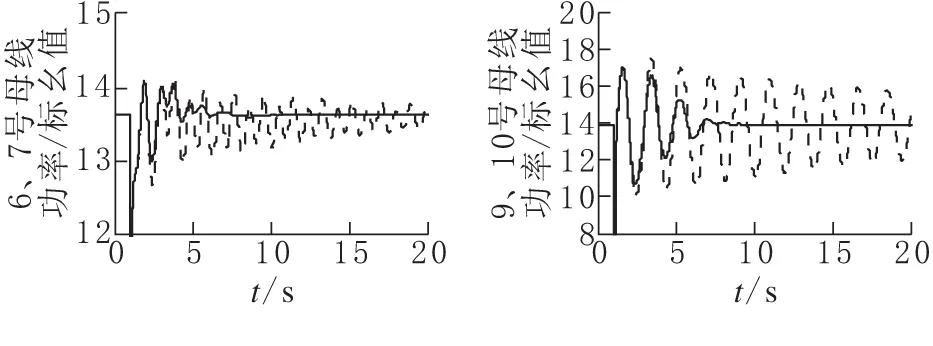
(c)母线11发生短路故障

3 实际系统阻尼振荡的仿真研究

图8为华中-华北互联系统的简单示意图。特高压电网建设初期，华中、华北两大区域电网仅通过一条特高压线路互联，属于典型的长链式弱联系系统。本节着重对大规模电力系统中，粒子群算法优化储能装置控制器的适用性进行仿真分析。

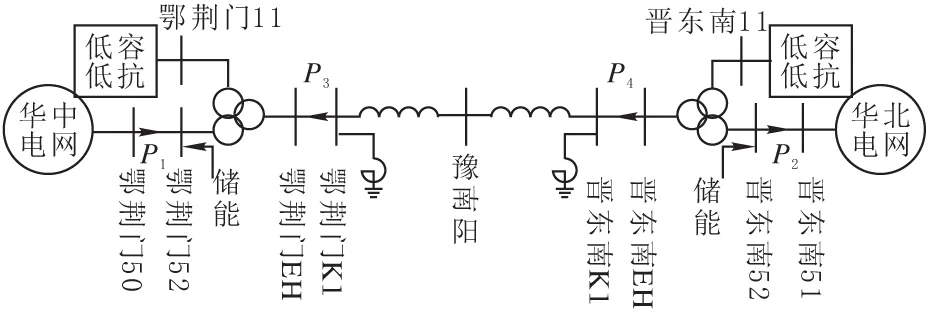
图8 华中-华北互联系统简单示意图

将储能装置安装在“鄂荆门52”母线和“晋东南52”母线上。按照2.3节联络线功率反馈控制的方法，分别以联络线功率P3和P4作为储能装置的输入信号，监测特高压联络线两端功率振荡情况。

分别模拟“鄂兴隆～鄂江陵”线路、“川洪沟～川普提”线路和“豫嵩山～豫郑州”线路故障，通过粒子群算法对两个储能装置的控制器进行优化，得到特高压联络线两端功率振荡情况如图9所示。

(a)“鄂兴隆～鄂江陵”线路故障

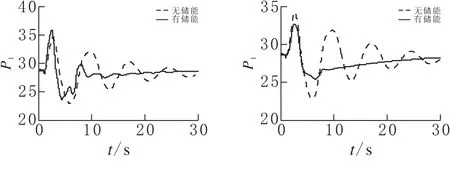
(b)“川洪沟～川普提”线路故障

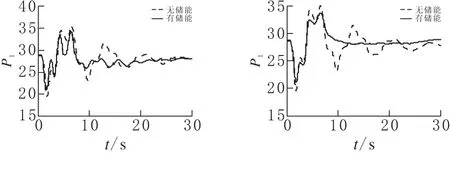
(c)“豫嵩山～豫郑州”线路故障

实际系统的仿真结果表明，不同故障下，储能装置对特高压联络线两端的功率振荡均具有较好的抑制效果，表明本文提出的粒子群算法优化储能装置控制器的方法在大规模电力系统中具有适用性。

4 结论

本文提出了一种利用粒子群算法优化储能装置控制器的方法。针对粒子群算法的搜索特点，自适应调节惯性权重系数以提高算法的收敛速度和收敛精度。介绍了本文所提优化方法的流程，重点在四机两区域系统中研究了储能装置安装位置的选择，并进一步利用联络线功率反馈作为控制器的输入，分析不同故障情况下储能装置对功率振荡的抑制效果。最后在华中-华北互联系统上进行了仿真，仿真结果表明，此方法在大规模电力系统中具有适用性。

[1] 杨慧敏．区域电网低频振荡特性分析与抑制方法研究[D]．武汉：华中科技大学，2005．

[2] 杜文娟，王海风．应用储能系统抑制电力系统低频振荡原理研究[J]．电力科学与技术学报，2008，23(01)：31-35，55．

[3] 王 康，兰 洲，甘德强，等．基于超导储能装置的联络线功率控制[J]．电力系统自动化，2008，32(08)：5-9．

[4]Mohd.HasanAli,ToshiakiMurata,andJunjiTamura.TransientStabilityEnhancementbyFuzzyLogic-ControlledSMESConsideringCoordinationWithOptimalReclosingofCircuitBreakers[J].IEEETrans.PowerSystem, 2008, 23(02): 631-640.

[5]Mohd.HasanAli,ToshiakiMurata,andJunjiTamura.AFuzzyLogic-ControlledSuperconductingMagneticEnergyStorageforTransientStabilityAugmentation[J].IEEETrans.ControlSystemsTechnology, 2007, 15(01): 144-150.

[6]J.Kennedy,R.C.Eberhart.ParticleSwarmOptimization[C].Proc.IEEEInt′l.Conf.onNeuralNetworks, 1995, 1942-1948.Piscataway,NJ:IEEEServiceCenter.

[7] 唐剑东，熊信银，吴耀武，等．基于改进PSO算法的电力系统无功优化[J]．电力自动化设备，2004，24(7)：81-84．

[8]TANGJiandong,XIONGXinyin,WUYaowu,etal.PowerSysterReactivePowerOptimizationBasedonModifiedParticleSwarmOptimizationAlgorithm[J].ElectricPowerAutomationEquipment, 2004, 24(07):81-84.

[9]FengCS,CongS,FengXY.ANewAdaptiveInteriaWeightStrategyinPartacleSwarmOptimization[C].ProcoftheIEEECongressonEvolutionaryComputation.Singapore, 2007: 4 186-4 190.

[10]KunderP.Powersystemstabilityandcontrol[M].NewYork,USA:McGraw_Hill, 1994.

[11] 林宇峰，徐 政，黄 莹．TCSC功率振荡阻尼控制器的设计[J]．电网技术，2005，29(22)：35-39．

[责任编校： 张岩芳]

Energy Storage Controller Optimization Based on Particle Swarm Algorithm

CHENG Xin

(GuangDongPowerGridDevelopmentResearchInstituteCo.,Ltd,Guangzhou510080,China)

Based on particle swarm algorithm, an optimization method for the energy storage controller was proposed. Compared with traditional methods, the proposed method averts sophisticated mathematical calculation. The method was simulated in the two-area four-machine power system model. The effect of dampening power oscillation of the energy storage under various faults was also analyzed using the tie-line power as the inputs of the energy storage controller. The simulation indicates that the optimization method is valid and can be applied in large-scale power systems.

energy storage; power oscillation; particle swarm algorithm; controller optimization

2014-07-18

程 鑫(1987-)， 男， 湖北黄石人，工学硕士，研究方向为电网规划

1003-4684(2015)01-0018-05

TM773

A