流动状态下铝粉爆炸过程的数值模拟
2015-05-10沈世磊陈嘉琛马秋菊
沈世磊, 张 奇, 陈嘉琛, 马秋菊, 李 栋, 闫 华
(1. 北京理工大学爆炸科学与技术国家重点实验室, 北京 100081; 2. 第二炮兵装备研究院, 北京 100094)
1 引 言
铝粉作为含能材料,广泛应用于燃料空气炸药中,其在空气中的爆炸特性是燃料空气炸药组分设计的基础。目前,铝粉在空气中爆炸的实验和数值模拟的研究成果较多,Zhang等[1]理论研究了铝粉爆炸实验中爆炸压力上升速率的递归计算方法。谭汝媚等[2]通过实验表明铝粉点火存在一个最佳点火时间,且随着铝粉浓度的增大,最佳点火延迟时间先增加后保持不变。陈志华等[3]数值研究了大型卧式燃烧管内铝粉颗粒与空气的两相悬浮流湍流燃烧加速转爆炸现象。但是铝粉流动状态和粒度对爆炸参数影响的数值模拟目前只有少量的文献报道[4-5]。文献[4-5]模拟了铝粉在密闭容器内的扩散过程,但并未解决人们更为关心的流动状态下铝粉在密闭容器内燃烧爆炸过程的数值模拟。
基于此,本研究利用流体计算软件 FLUENT[6]模拟了粒径为7~42 μm的铝粉在20 L圆柱型爆炸装置内扩散以及爆炸过程,并将数值模拟与文献结果进行了分析和比较,以期得到流动状态下铝粉粒度对爆炸参数的影响。
2 模型建立
2.1 二维模型建立
模拟实验装置[7]如图1所示, 为了简化计算,本研究对模拟对象进行了修改,将喷头移至上下底面,利用容器的轴对称性将20 L圆柱型爆炸装置简化为柱坐标系下的二维模型(图2中X和Y表示轴向和径向),边界条件设置及网格划分如图2所示。通过网格验证计算得到,当选用三角形结构网格时,网格数目为148602个计算结果稳定。
2.2 物理化学模型假设
Young-Soon Kwon等[8]对铝粉的燃烧机理做了详细的阐述,本研究将铝粉的燃烧过程简化为一步反应: 2Al+3/2O2→Al2O3。由粉尘爆炸机理[9]可知粉尘爆炸是粉尘颗粒表面分子受热分解或干馏作用,而变为气体分布在粒子周围,其实质是气体爆炸,所以不考虑铝粉颗粒表面生成氧化膜。本研究所计算铝粉的粒径(微米级)较小,铝粉扩散过程中考虑气体和颗粒之间的相互作用,忽略颗粒之间的碰撞作用[10],考虑重力作用,不考虑其它力的作用[10]。
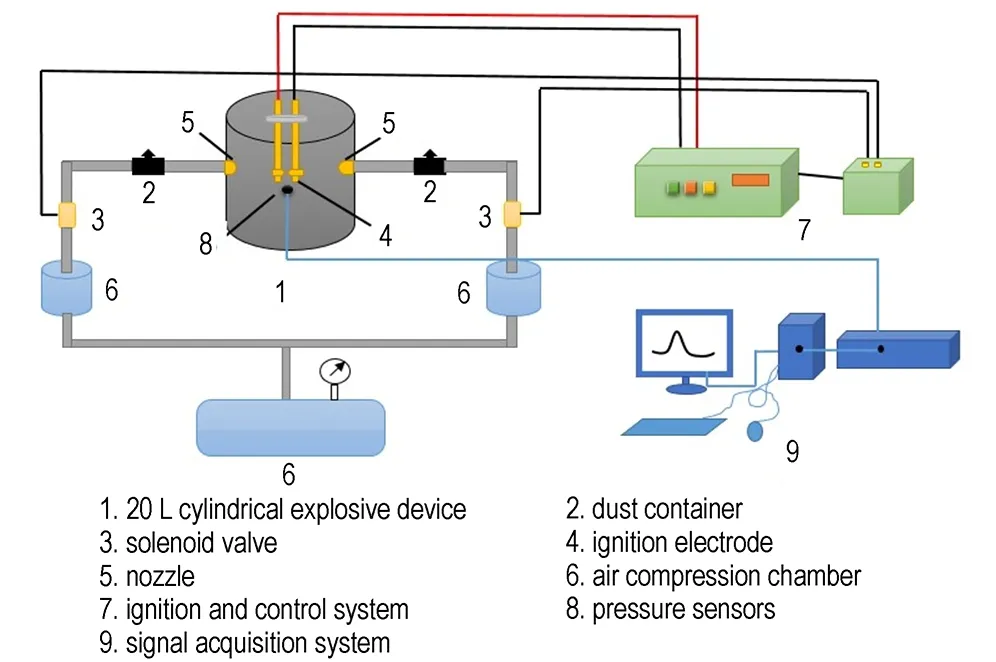
图1 模拟计算的实验装置[7]
Fig.1 Experimental apparatus of simulation[7]
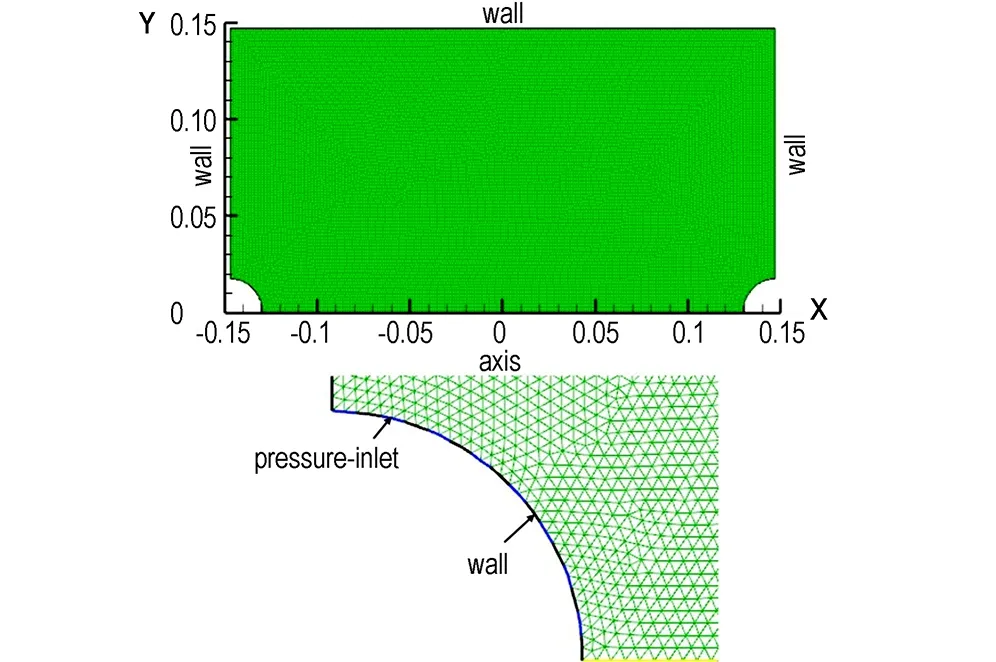
图2 简化模型的边界条件及网格划分
Fig.2 Boundary conditions and mesh generation of the simplified mode
2.3 控制方程
粉尘的扩散可以考虑为两相流问题,本研究气相流动控制方程采用稳态不可压N-S方程[6],使用SIMPLE算法[6]对气相流场进行求解; 湍流流动模型采用标准κ-ε模型[6]; 颗粒选用离散相模型(DPM)[6]通过积分拉式坐标下的颗粒作用力微分方程来求解粉尘颗粒的轨道,采用斯托克斯追踪(随机轨迹)轨迹模型[6],颗粒所受作用力平衡方程在笛卡尔坐标系下的形式[6]为:
(1)
式中,u为气相速度,m·s-1;up为颗粒速度,m·s-1;ρ为气体密度,kg·m-3;ρp为颗粒密度,kg·m-3;FD(u-up)为颗粒的单位质量拖拽曳力,N;Fx为附加质量力,N。
式(1)中:
(2)
(3)
式中,μ为流体动力粘度,Pa·s;dp为颗粒直径,m;Re为相对雷诺数(颗粒雷诺数);CD为拖曳力系数,且有,
(4)
(5)
由于颗粒粒径较小,受到的流体曳力是最主要的,其次是重力,其他力一般可以忽略不计[11]。
模拟铝粉的燃烧选用有限速率/涡耗散(Finite-Rate/Eddy-Dissipation)模型[6],铝粉的化学反应速率(VAl,A)可写成质量分数的Arrhenius形式[11]:
(6)
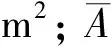
湍流脉动机制所控制的燃烧速率为:
(7)
式中,CEBU为常数;ε为湍流脉动动能耗散率;κ为湍流脉动动能,J。
根据EBU-Arrhenius燃烧模型,罐内铝粉燃烧速度为:
V=min(|VAl,A|, |VAl,T|)
(8)
辐射模型采用DO(Discrete Ordinates)模型[6],同时考虑散射的影响以及气体和颗粒之间的辐射传递。
2.4 参数设置
本研究数值模拟的点火位于装置中心,点火源设为圆形高温区域。其他参数如表1。
表1 铝粉扩散及爆炸数值模拟参数
Table 1 Simulation parameters of diffusion and explosion for aluminum dust

parametersvalueairtemperature/K300airpressure/Pa1.01325×105pressureofblowingdust/Pa5.01325×105timeofblowingdust/ms10ignitiondelaytime/ms60aluminumdensity/kg·m-32719aluminumheatofcombustion/J·kg-13.1×107activationenergy/MJ·mol-182pre⁃exponentialfactor/(m3·kg)1/2·s3.8×105wallheatcapacity/J·kg-1·K-1480wallthermalconductivity/W·m-1·K-148ignitiontemperature/K2500ignitionradius/cm1
3 结果讨论
3.1 扩散过程模拟
为了监测粉尘的运动路径,绘制了圆柱罐内颗粒在不同时刻(5,15,25,35,45 ,60 ms)的轨迹。图3为通过颗粒浓度分布来显示离散相颗粒位置随时间的变化,其中铝粉粒径为11 μm、浓度为500 g·m-3。图4为容器内不同时刻(5,15,25,35,45 ms和60 ms)的湍流动能,从图4中可以看出湍流动能随时间逐渐降低。从图3和图4中可以看出60 ms时铝粉的分布已较为均匀,沉降作用不明显,铝粉的运动主要受湍流影响。因此本研究模拟铝粉爆炸时选择60 ms作为点火延迟时间较为合理。
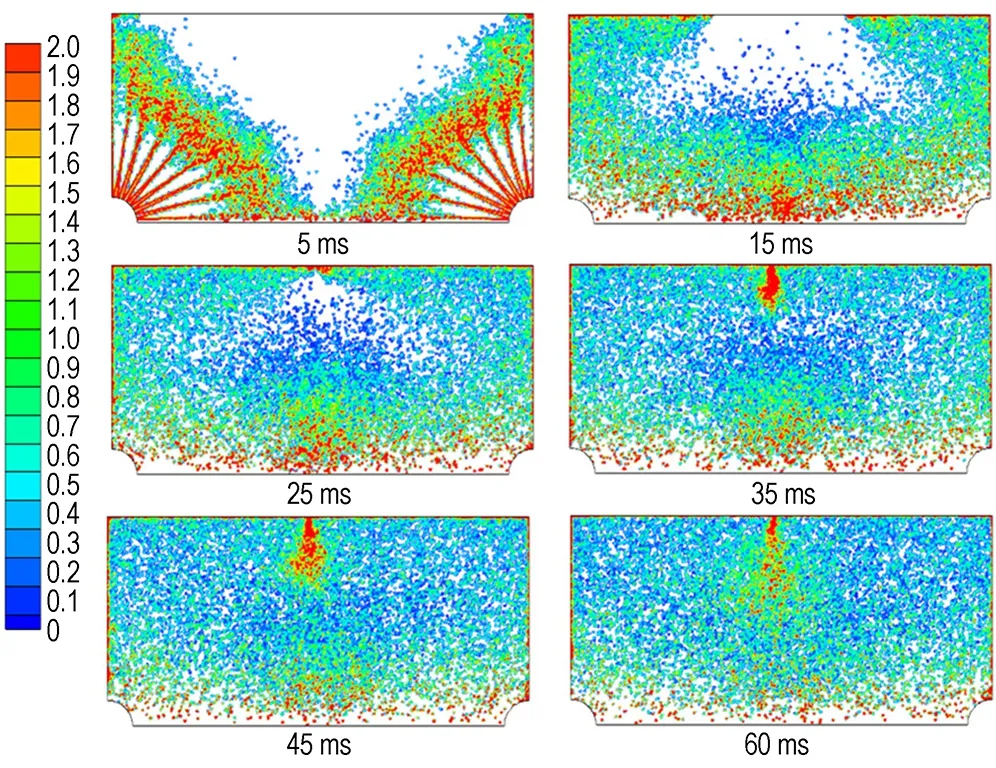
图3 容器内铝粉在不同时刻的浓度分布(单位: kg·m-3)
Fig.3 Concentration profile of aluminum dust in chamber at different time(unit: kg·m-3)
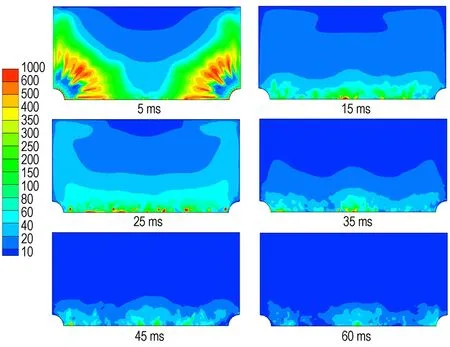
图4 容器内不同时刻的湍流动能(单位: m2·s-2)
Fig.4 Turbulence kinetic energy in chamber at different time (unit: m2·s-2)
3.2 爆炸过程模拟
图5为数值模拟爆炸过程时得到的典型的温度场变化,从图5可以看出,火焰从初始时刻的点火区域逐渐向四周扩散。爆炸前期,火焰形态不规则,主要是因为铝粉扩散时湍流强度以及颗粒自身的运动作用影响较大,导致燃烧时火焰面被褶皱和拉伸。随着爆炸过程的发展,火焰形态开始变得规则,呈近似球形。这一点与实际情况相符。从图5中还可以看出燃烧区域与未燃烧区域之间存在一个约为3 mm厚的预热区域,这一点与利用纹影技术所测情况[12]相符。
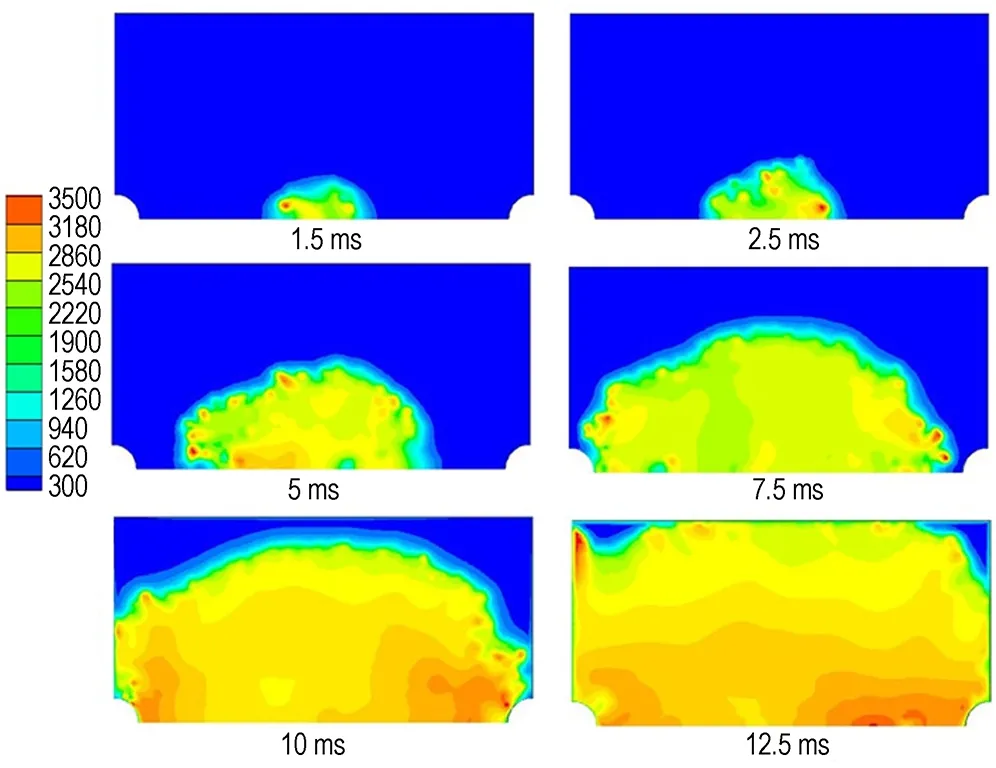
图5 铝粉爆炸后容器内温度场变化(单位: K)
Fig.5 Temperature field changes of the chamber after aluminum dust explosion(unit: K)
3.3 火焰速度模拟
利用温度场和颗粒分布随燃烧时间的变化图,计算了浓度为500 g·m-3、粒径为11 μm的铝粉燃烧时容器径向(图2中Y方向)的火焰速度,如图6所示。从图6可以看出,火焰传播速度沿径向的变化趋势为先降后升再降(最大值为150.9 cm·s-1,最小值为70 cm·s-1)。这是因为前期湍流扰动[14]和颗粒自身运动对火焰传播的影响较大,中期这一影响减弱,铝粉开始稳定燃烧,随着容器内压力的逐渐增大,速度呈缓慢上升趋势,与文献[13]吻合,后期由于壁面阻碍了火焰的传播使速度急剧下降。
浓度为500 g·m-3时,粒径分别为7,11,27,42 μm铝粉爆炸时,罐壁面中心处A点(图1传感器所在位置)的压力随时间变化见图7。从图7中可以看出,铝粉粒径为7~42 μm,铝粉爆炸的最大压力(pmax)及最大压力上升速率((dp/dt)max)随粒径增大而减小,pmax和(dp/dt)max最大值分别为0.876 MPa和120.1 MPa·s-1,最小值分别为0.634 MPa和19.5 MPa·s-1,这是由于随着粒径的增大,粉尘的沉降作用也越来越大,影响了燃烧反应的程度。该规律与文献 [15]所得情况相符。图8为不同粒径下最大爆炸压力和最大爆炸压力上升速率的模拟值和实验值[15]的比较,最大压力pmax和最大压力上升速率(dp/dt)max的模拟值与实验值最大相对误差分别4.6%和20%。
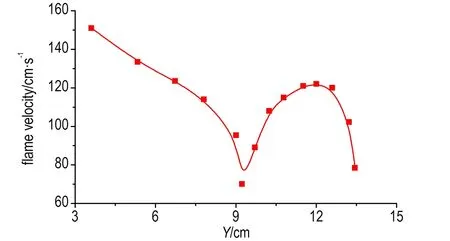
图6 容器径向不同位置的火焰传播速度
Fig.6 Flame propagation velocity along radial direction of vessel
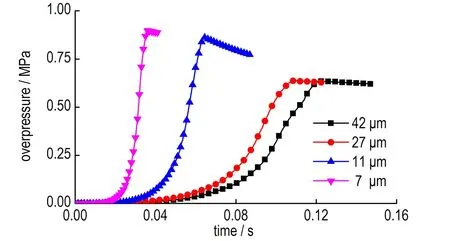
图7 不同粒径铝粉爆炸压力随时间的变化曲线
Fig.7 Curves of explosion pressure of aluminum with different particle size vs time
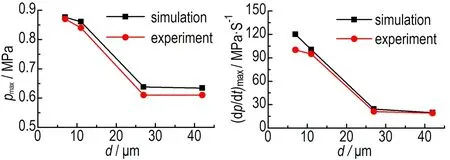
a. maximum explosion pressure b. maximum explosion pressure rise rate
图8 不同粒径下铝粉爆炸压力特性的模拟值与实验值对比
Fig.8 Comparison between simulated and experimental values of aluminum dust explosion pressure characteristics with different particle size
4 结 论
(1) 当点火延迟时间为60 ms时,容器的径向火焰传播速度的变化趋势为先降后升再降,最大值为150.9 cm·s-1,最小值为70 cm·s-1。
(2)由铝粉爆炸时火焰速度变化规律可知,前期湍流以及颗粒自身的运动对火焰发展影响较大,因此利用实验研究铝粉爆炸机理,尤其是火焰速度时,必须考虑湍流的影响。
(3)铝粉粒径为7~42 μm时,随着粒径的增加,最大爆炸压力pmax和最大爆炸压力上升速率(dp/dt)max逐渐减小,pmax和(dp/dt)max最大值分别为0.876 MPa和120.1 MPa·s-1,最小值分别为0.634 MPa和19.5 MPa·s-1,模拟结果与文献吻合,pmax和(dp/dt)max与实验值最大相对误差分别为4.6%和20%。
参考文献:
[1] ZHANG Qi, MA Qiu-ju, ZHANG Bo. Approach determining maximum rate of pressure rise for dust explosion[J].JournalofLossPreventionintheProcessIndustries, 2014, 29: 8-12.
[2] ZHANG Qi, TAN Ru-mei. Effect of aluminum dust on flammability of gaseous epoxy propane in air[J].Fuel, 2013, 105: 512-517.
[3] 陈志华, 范宝春, 李鸿志. 燃烧管内悬浮铝粉燃烧爆炸过程的研究[J]. 高压物理学报, 2006, 20(2): 157-161.
CHEN Zhi-hua, FAN Bao-chun, LI Hong-zhi. Investigation on Combustion and Explosion Process of Suspended Aluminum Particles in a Large Combustion Tube[J].ChineseJournalofHighPressurePhysics, 2006, 20(2): 157-161.
[4] 陈嘉琛, 张奇, 马秋菊, 等. 20 L球型罐内不同粒径铝粉扩散的数值模拟[J]. 高压物理学报, 2014, 28(2): 202-208.
CHEN Jia-chen, ZHANG Qi, MA Qiu-ju, et al. Numerical simulation of aluminite dust dispersion for different particle sizes[J].ChineseJournalofHighPressurePhysics, 2014, 28(2): 202-208.
[5] Sarli V Di, Russo P, Sanchirico R, et al. CFD simulations of dust dispersion in the 20 L vessel: Effect of nominal dust concentration[J].JournalofLossPreventionintheProcessIndustries, 2014, 27: 8-12.
[6] Fluent Incorporated. Fluent 6.3 User′s Guide[M]. Cavendish: Fluent Incorporated, 2006.
[7] LIU Xue-ling, ZHANG Qi, WANG Yue. Influence of Vapor-Liquid Two-Phase n-Hexane/Air Mixtures on Flammability Limit and Minimum Ignition Energy[J].Industrial&EngineeringChemistryResearch, 2014, 53: 12856-12865.
[8] Kwon Young-soon, Alexander A, Gronmov, et al. Ilyin, et al. The mechanism of combustion of superfine aluminum powders[J].CombustionandFlame,2003,133: 385-391.
[9] 赵衡阳. 气体和粉尘爆炸原理[M].北京: 北京理工大学出版社, 1996.
ZHAO Heng-yang. Principles of Gas and Dust Explosion [M]. Beijing: Beijing Institute of Technology Press, 1997.
[10] Elghobashi S. On predicting Particle-Laden turbulent flows[J].AppliedScientificResearch, 1994, 52: 309-329.
[11] 王福军. 计算流体动力学分析[M]. 北京: 清华大学出版社, 2004.
WANG Fu-jun. Computational Fluid Dynamics Analysis[M]. Beijing: Tsinghua University Press, 2004.
[12] Crowe C T, Ttoutt T R, Chung J N. Numerical Models for Tow-Phase Turbulent Flows[J].AnnuRevFluidMech, 1996, 28: 11-43.
[13] Jinhua Sun, Ritsu Dobashi, Toshisuke Hirano. Structure of flames propagating through aluminum particles cloud and combustion process of particles[J].JournalofLossPreventionintheProcessIndustries, 2006, 19: 769-773.
[14] 李新光, 张平, Radandt S, 等. 20 L球形装置上粉尘湍流速度的测量[J]. 东北大学学报(自然科学版), 2003, 24(10): 952-955.
LI Xin-guang, ZHANG Ping, Radandt S, et al. Measurement of Turbulence Velocity of Dust in a 20 L sphere[J].JournalofNortheasternUniversity(NaturalScience), 2003, 24(10): 952-955.
[15] Dufaud O, TraoréM, Perrin L, et al. Experimental investigation and modelling of aluminum dusts explosions in the 20 L sphere[J].JournalofLossPreventionintheProcessIndustries, 2010, 23: 226-236.
