Molecular Dynamics Simulations of Crystalline δ-HMX with Void Defect

LIAO Ning, LI Wen-peng, ZHOU Xiao-qing, DUAN Xiao-hui

(1. State Key Laboratory Cultivation Base for Nonmetal Composites and Functional Materials, Southwest University of Science and Technology, Mianyang 621010, China； 2. Institute of Chemical Materials, China Academy of Engineering Physics, Mianyang 621999, China)

1 Introduction

As an important energetic material,octahydro-1, 3, 5, 7-tetranitro-1, 3, 5, 7-tetrazocine (C4H8N8O8, HMX) has four known crystalline phases, namely,α,β,δandγ. It has been observed that theδform has 4 coplanar carbon atoms with aC2axis;α-HMX has aC2axis, andβ-HMX has a center of inversion symmetry[1]. The stabilities of the crystalline forms at room temperature areβ>α>γ>δ, the same as the order of the densities[2]. When heated to temperatures above 435 K, the monoclinicβ-HMX converts to the hexagonalδmorphology[3-4], the most reactive phase[5-6]. For the transformation fromβphase toδphase, it involves major changes of both the crystal lattice and the molecular ring conformation[3-6]. Accompanying the transition process is that a significant lattice expansion[7]results in an appearance of cracks and large amount of hot spots in the material and the fast growth of reaction during shock compression[8]. Those can be contributed to sensitivity increase of theδphase[3-4,8]. The decomposition of theδ-HMX practically coincides with theβδphase transition and the possible decomposition of theβ-phase.

Many experimental reports declare a high sensitivity ofδphase, atomistic theoretical investigations are scarce[9-11]. Many factors, such as density, defects, electronic excitations, and particle sizes, suggest to contribute to the sensitivity of energetic materials. Among them, defects including voids, molecular vacancies, dislocations, surface, and interfaces etc. play a crucial role to initiate explosive decomposition reactions, referred to as sensitivity. At present, the investigations on defect effects mainly focus on theβ-HMX[12-14], and only a literature had studied the surface-accelerated decomposition ofδ-HMX[15]. These investigations have indicated that the surfaces, interfaces, voids, or vacancies can lower the activation barriers and accelerate kinetics of decomposition of HMX. Seeing that the special function ofδphase in the initial reaction of decomposition, dynamics characterization ofδ-HMX containing defects are very important to further understand the reaction mechanism of HMX.

In our previous work[14], we investigated the void defects contained in crystallineβ-HMX. Void collapse observed with runtime was promoted by the change of the strain field and the increased system pressure due to applying canonical ensemble (NVT). In this paper, aimed at gaining a better understanding of molecular dynamics characterization of void defects, we further researched the void defects in crystallineδ-HMX applying NPT (normal pressure and temperature) simulations, including the activation barriers for an isolated molecule, void evolvement, and molecular conformations change along with simulation time. This investigation may provide some atomistic details for the observed sensitivity increase of theδphase compared to theβphase and the degradation mechanism of HMX.

2 Methodology

The structure of crystallineδ-HMX is hexagonal and belongs to the space group P61. The unit cell of the crystal is shown in Fig.1. The initial structure was created using the crystallographic data from Ref. 4. In theδ-phase lattice, each C4H8N8O8molecule has a boat conformation, having all four NO2groups on the same side of the C4N4ring (Fig.1). According to neutron diffraction experiments ofβ-HMX[16], we constructed the unit cell model presented in Fig.1.β-lattice belongs to monoclinic space groupP21/cand contains 2 independent HMX molecules in unit cell. Eachβ-HMX molecule presents chair form and has a symmetry center. Theβ-HMX molecule with central symmetry has lower energy thanδ-HMX molecule withC2symmetry. The super-cells used for simulation of void defects are composed of 5×5×2 unit cells forδcrystal and 5×5×6 forβone (300 molecules, 8400 atoms). After that, cohesive voids were introduced by removing 30 molecules from the 300-molecules super-cell, first one and its neighbors over an increasing distance; this corresponds to a 10% concentration of vacancies in the material.

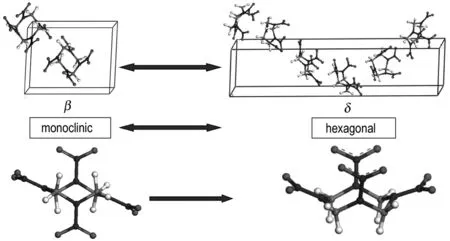
Fig.1 Unit cell structures forβandδphases and HMX molecular conformations inδandβphases. Legend: carbon-gray, hydrogen-white, nitrogen-blue, oxygen-red

The active energy barriers were determined by the QST3 method, which searched for the transition structure using the Synchronous Transit-Guided Quasi-Newton (STQN) method. This method was developed by H. B. Schlegel and coworkers[17-18], and it uses a linear synchronous transit or quadratic synchronous transit approach to get closer to the quadratic region around the transition state and then uses a quasi-Newton or eigenvector-following algorithm to complete the optimization. Density function theory (DFT) method combined with 6-31++G (d, p) basis set and B3LYP functional was applied. Convergence criterion was set to be “tight”. Firstly, the geometry optimization was performed at the B3LYP/6-31++G (d, p) level. Secondly, the search for the transition state was carried out by QST3 method. Finally, the harmonic vibrational frequencies were calculated based on the optimized geometries. All quantum chemical calculations were completed through the Gaussian software[19].

The dynamics characterization of void defectwas investigated by a MD simulation. A large number of literatures have indicated that the COMPASS (condensed-phase optimized molecular potentials for atomistic simulation studies) force field[20]can be effectively applied to the theoretical simulations for the crystalline HMX[14, 21-24]. Therefore, COMPASS force field was used in our simulations. Experimental,δ-HMX is stable in the temperature range of 433-553 K[25]andβ-HMX under room temperature at an atmospheric pressure[2, 25-26]. Besides, the melting point ofβ-HMX is in the range of 540-550 K due to different determined methods. So, the simulation temperatures were set to be 200, 300 K and 500 K, containing the stable and unstable temperatures for two forms. The Coulombic and van der Waals interactions were calculated by the standard Ewald method with quality “fine”[27]. The charge was calculated using the QEd method[28]. The basis of this method is the equilibration of atomic electrostatic potentials with respect to a local charge distribution. The NPT ensemble was applied with a time step of 1 fs. Temperature was controlled using the Nose thermostat and pressure by Berendsen method. The system was simulated over a total time of 1ns and the trajectory was output every 5000 time steps. The simulation was run with the commercial molecular modeling software package Materials Studio 3.0[29].

3 Results and Discussion

3.1 Active Barriers of Conformational Transitions in Vacuum

Four unique low-energy conformers were found for HMX molecule in vacuum, two whose conformational geometries correspond closely to those found in HMX polymorphs,βandα, and two additional, lower energy conformers that are not seen in the crystalline phases, boat-chair (BC) and boat-boat (BB)[30]. The relative energies of all conformers of an isolated molecule can be found in literature [30], namely,α>β>BB>BC. These conformations are known to exist within a narrow interval of energies.

In this work, the energies of transition states for the conformational transitions were obtained by the QST3 method at the level of B3LYP/6-31++G(d, p). The calculated active barriers were listed in Table 1 with the correction of quantum zero-point vibrational effects. The frequency calculations indicate that there is one and only one imaginary frequency for all the transition structures, and the four conformers, namely,α,β, BB, and BC, have no any imaginary frequencies. Therefore, we can determine the structures obtained by the QST3 method corresponding to the transition states.

From the active barriers listed in Table 1, we can find that the transitions from other conformations to BC have lower active barriers. Specially, the barrier fromαto BC is negative, which means this conversion is very favorable in energy. In all possible transitions, the value of the highest energy barrier for theβBB conversion is 33.22 kJ·mol-1. Secondly, the barrier fromβtransits to α is 32.72 kJ·mol-1. The two barriers are approximately 7 times higher thanRTat 500 K. Other barriers are much lower than the two values. Based on the Arrhenius equation, we predict that all conversions may easily take place thermodynamically.

Table 1 Active barriers of the conformation transitions (in kJ·mol-1)

transitionsβ⇆αβ⇆BBβ⇆BCα⇆BBα⇆BCBB⇆BCforward32.7233.2210.3321.46-3.644.85backward21.4625.569.5825.565.449.58

3.2 Dynamics Evolvement of Void

For the MD simulations at different temperatures,we have observed the different evolvement trends of voids inserted into two different forms,δandβ(see Fig.2). Forδpolymorph, the void has been completely collapsed at three temperatures. At 200 K and 300 K, the molecules collapsed into the void present the characteristics of partial order, but when the temperature increases up to 500 K, not only the molecules near the void but also the whole lattice melt into the liquid state. This can be further verified by the mean square displacement (MSD) analysis later (see Fig.3). Under low temperatures of 200 K and 300 K, except for the molecules located at or near the surface of a void, the whole lattice has also large change, losing strictly periodic structure seen from Fig.2. However, forβphase, at the temperatures of 200 K and 300 K, the void is still hold on, only the shrink of void and some shift of molecules toward the center of void occur due to the change of the strain field. When the temperature is up to 500 K, the case is the same as theδphase, namely, the whole lattice completely collapsed into liquid state.

Compared to initial model, the density and volume of system have changed after 1ns MD simulations. Under low temperatures of 200 K and 300 K, the lattice shrink ofδ-HMX results in the decrease of volume and the increase of density. For example, the density increases from 1.67 g·cm-3to 1.70 g·cm-3at 300 K and 1.73 g·cm-3at 200 K. The volume change accompanying void collapse is 1.53% and 3.20%, respectively. However, when the simulated temperature goes to 500 K, the lattice expands approximately 10.5%. Accordingly, the density reduces down to 1.51 g·cm-3. Different fromδ-HMX, the volume ofβ-HMX is on the increase with the simulated temperature. When the temperature changes from 200 K to 500 K, the volume grows from 2.1% to 16.4%. At 500 K, despite ofβorδphase, the system completely melts into liquid state and has the same density -1.15 g·cm-3.

The different evolvement trends result from the different lattice arrangements and intermolecular interactions. The experimental value for heat of sublimationHsubis 184.76 kJ·mol-1and 175.90 kJ·mol-1for theβandδphases, respectively[31-32]. Structural stability and sublimation enthalpy are very useful for understanding the safety of HMX in different crystal phases. More sublimation enthalpy means that the system needs more energy to overcome the lattice bounding and inter- and intra- interactions when the solid energetic materials convert into small gaseous molecules. Besides, the formation energy of a void defect with sizen,Ef(n), is also illustrated the different evolvement trends ofδandβphases.Ef(n) was calculated according to the method in Ref [33]. The value forEf(30) in crystallineδ-HMX is calculated to be 6833.35 kJ·mol-1, and the formation energy per molecule removed,Ef(n)/n, is 227.78 kJ·mol-1. Applying the same method, this value ofEf(30) forβ-HMX is 7009.66 kJ·mol-1,Ef(30)/30 equals to 233.66 kJ·mol-1. These quantitative values indicate the difference in the crystal lattice, the molecular conformation, and the microstructure of two crystalline phases. At the same time, it has also illustrated thatβ-HMX is more stable thanδphase. Our MD simulations show that theβ-HMX containing a void defect is still more stable thanδ-HMX with the same size void. Generally, the so-called “hot spots” in energetic materials are mainly the local regions of a crystal (crystal defects or deformations). Voids, molecular vacancies, dislocations, pore, impurities, and other types of defects play a crucial role in initial reactions. According to hot spots theory, the initiation of combustion in energetic materials is associated with “hot spots”, in which collapse of voids may be one of the most important mechanisms the leads to ignition in pressed explosives. So, the different evolvement trends also give some atomistic details for the observed sensitivity increase of theδphase compared to theβphase and the initial reaction mechanism of HMX.

a.δ, 200 K b.δ, 300 K c.δ, 500 K

d.β, 200 K e.β, 300 K f.β, 500 K

Fig.2 Final geometries forδandβphases containing a void defect after 1 ns NPT simulations at 200, 300 K and 500 K, respectively

The behavior of MSD as a function of time is presented in Fig.3 and Fig.4. The data in the range of 600-1000 ps were used to plot the MSD curve. The behavior of MSD as a function of time can be used to discriminate between a solid and a liquid phase. The MSD of the solid system oscillates about a mean value. For a fluid, without underlying regular structure, the MSD gradually increases with time. So, from Fig.3, we can see that theδ-HMX crystal with a void defect presents part liquid-state feature at 200 K and 300 K, which is agreement with the geometries shown in Fig.2. When simulated temperature rises to 500 K, the system exhibits normal linear diffusive behavior, and this means that the lattice has completely collapsed into liquid state. Diffusion coefficient (D) is calculated by the well-known Einsteins relation, which obtains diffusion coefficients as a tangent of the linear region of the displacement function. The Einsteins relation is expressed as:

(1)

whereri(t) denotes the position vector at timet,ri(t0) the position vector at time origin, the angular bracket denotes averaging over all choices of time origin within a dynamics trajectory, andNis the total number of the diffusion particles. The diffusion coefficient at 500 K was calculated to be 1.2×10-10m2·s-1, significantly above the diffusion coefficient of baseline molecular of the order of 10-12m2·s-1. This value is observed for a molecule in the defect-free lattice and restricted to thermal fluctuations around its equilibrium site.

Forβphase, the MSD curves are shown in Fig.4. At the temperature of 200 K, MSD oscillates about a mean value, showing an obvious solid-phase characteristic. At 300 K, we can still observe the oscillation phenomenon, but the MSD value increases slowly with runtime, indicating the lattice binding slightly reduces. When temperature rises up to 500 K, the case is very similar with theδ-HMX. Namely, the system finally changes into liquid state after 1 ns MD simulation. The difference is that normal linear region appears only after approximately 800 ps. This illustrates the rate of lattice collapsing is slower than that ofδphase. Besides, the diffusion coefficient is determined using the data of linear region 800-1000 ps, and the value is 1.5×10-10m2·s-1, almost the same as that ofδphase.

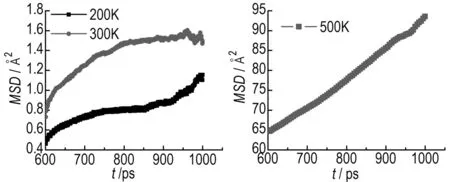
a. 200 K, 300 K b. 500 K

Fig.3 Calculated MSD forδ-HMX system containing a void defect at different temperatures

a. 200 K, 300 K b. 500 K

Fig.4 Calculated MSD forβ-HMX system containing a void defect at different temperatures

3.3 Conformational Transition of Single Molecule with Time

For collapsed liquid-state molecules, tracing the single molecule along with runtime, it can be observed the frequent transitions of molecule between different conformations. To illustrate this, we cut out a section of snapshots from MD simulation with a time period of 20 ps (see Fig.5). During 20 ps runtime, we have observed the obvious conformation transitions, namely from BB toα. Besides, we captured the transition state or intermediated structures undergone by this conversion, presenting the reversion of two downward NO2groups and adjustment of ring structure. When the system hasn′t completely melted into liquid state, for example the molecules collapsed into the void inδcrystal lattice under 200 K and 300 K, we can still observe the conformational transition, but the conversion rate is much slower due to the effects of the crystal field.

The frequent transitions can be explained by the active barriers and the formation energy of the void defect. In section 3.2, we had already calculated the formation energies of voids inserted intoβandδcrystal lattices, and they are 7009.66 and 6833.35 kJ·mol-1, respectively. Combined with the active barriers listed in Table 1, we can predict that the formation energy is enough to induce conformational changes, rotations, and center-of-mass translations of the molecules in system, and even the melting of crystal lattice.

Fig.5 Change of molecular conformations during 20 ps from the MD simulation for liquid-state system at 500 K

3.4 Conformational Distribution in Final Simulation System

At the simulation temperature of 500 K,no matterδorβphase, the system containing a void has collapsed into liquid state going through 1 ns simulation, and has the same density of 1.51 g·cm-3. So, we have thought the conformation distribution of final liquid system to be roughly similar for two crystal phases. And that is true through our conformational analysis. We find that some molecules are in stable conformations(about 40%), but a large number of molecules with transition state or intermediate structures(approximately 60%). In the different conformations, the ratio of BC is the largest(approximately 18%), next BB(approximately 12%), and the proportion ofαandβis relatively low(approximately 4% and 6%, respectively). The reason may be the combination of conversion barrier and the conformation stability. Such as, all the active barriers conversing to BC are relatively lower (see Table 1), and the energy of BC is the global minimum, which result in BC with highest ratio. Besides, a larger number of transition state and intermediate structures also make the collapsed system higher energy and more active. It can provide some evidence for the view that the collapse of voids seems to be one of the most important mechanisms that can lead to ignition in pressed explosives.

Under lower temperatures of 200 K and 300 K, for the molecules collapsed into the void inδphase, we observe the conformation of most molecules is not change, still keeping theαconformation, owing to the effect of crystal field. Secondly, the transition state and intermediate are dominant in the rest of collapsed molecules. Besides, minority molecules are found with BC or BB structure.

Forβphase, we have observed that the molecules on the surface of a void shift to the center of void at 200 K and 300 K from the Fig.2. The anisotropic interactions with others in their vicinities lead to variations in numbers and strengths of interactions as well as possible conformational changes. We find the conformational transition is mainly fromβto BC for the shifted molecules. It agrees with the lowest active barrier ofβ→BC among all transitions fromβto other conformations (10.33 kJ·mol-1, Table 1). Of course, the transition state and intermediates structures are also observed on the surface of void. These molecules have higher energy than that ofβ-HMX molecule, and will show more activity to initiate the degradation reaction of HMX. It had been demonstrated by DFT calculations coupled with transition state theory[12].

4 Conclusions

MD simulation for crystallineδ-HMX with a void defect was performed to study the dynamics characteristic of void evolvement and molecular conformation change, compared withβphase. The calculations for active energies of conformational transitions for the isolated molecules indicate that the higher barriers are 33.22 and 32.72 kJ·mol-1, and others are much lower than the two values. This means that all conversions can easily take place in energy.

MD simulation shows that the crystalline system containing 10% vacancy concentration completely collapses into liquid phase after 1 ns NPT simulation at 500 K, no matterδorβphase. Compared to initial models, the lattice expands result in the system density down to 1.51 g·cm-3. For the liquid system, four conformations, namely,α,β, BB, and BC, have been observed. Among them, the proportion of BC is the largest. Besides, a large number of transition state and intermediate molecules are observed. Tracing the single molecule along with the runtime, frequent transitions between conformational states are found due to low energy barrier.

At 200 K and 300 K, different evolvement trends are observed forδandβphases. Forδphase, the void has completely collapsed, and the whole crystal lattice has also lost the rigid periodicity. However, void and crystal lattice ofβphase have been hold on, and there only occur the shrink of void and some shift of molecules toward the center of void. Contrary to the volume shrink ofδphase, lattice expansion is observed forβphase. Besides, for the molecules collapsed into void or on the surface of void, except for the stable conformations, transition state or intermediate molecules have been found. Different evolvement behaviors of the voids contained inδandβphases may provide some important information to explain the sensitivity difference of two crystalline phases and the initial reaction mechanism of HMX.

[1] Cobbledick R E, Small R W H. The crystal structure of theδ-form of 1,3,5,7-tetranitro-1,3,5,7-tetraazacyclooctane (δ-HMX)[J].ActaCrystallographicaSectionB:StructuralCrystallographyandCrystalChemistry, 1974, 30(8): 1918-1922.

[2] Goetz F, Brill T B, Ferraro J R. Pressure dependence of the raman and infraredspectra ofα-,β-,γ-, andδ- octahydro-1,3,5-7-tetranitro-1,3,5,7-tetrazocine[J].TheJournalofPhysicalChemistry, 1978, 82(17): 1912-1917.

[3] Cady Howard H, Larson Allen C, Cromer Don T. The crystal structure ofα-HMX and a refinement of the structure ofβ-HMX[J].ActaCrystallographica, 1963,16(7): 617-623.

[4] Cobbledick R E, Small R W H. The crystal structure of the δ-form of 1,3,5,7-tetranitro-1,3,5,7-tetraazacyclooctane (δ-HMX)[J].ActaCrystallographicaSectionB:StructuralCrystallographyandCrystalChemistry, 1974,30(8): 1918-1922.

[5] Brill T B, Reese C O. Analysis of intra- and intermolecular interactions relating to the thermophysical behavior of .alpha.-, .beta.-, and delta, -octahydro-1,3,5,7-tetranitro-1,3,5,7-tetraazocine[J].TheJournalofPhysicalChemistry, 1980, 84(11): 1376-1380.

[6] Brill T B, Karpowicz R J. Solid phase transition kinetics. The role of intermolecular forces in the condensed-phase decomposition of octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine[J].TheJournalofPhysicalChemistry, 1982,86(21): 4260-4265.

[7] Henson B F, Asay B W,Sander R K et al. Dynamic measurement of the HMXβ-δPhase transition by second harmonic generation[J].PhysicalReviewLetters, 1999,82(6): 1213-1216.

[8] Urtiew P A, Forbes J W, Tarver C M, et al. Shock sensitivity of LX-04 containing delta phase HMX at elevated temperatures[C]∥Aip Conference Proceedings, 2004.

[9] Lewis J P. Energetics of intermolecular HONO formation in condensed-phase octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine (HMX)[J].ChemicalPhysicsLetters, 2003,371(5): 588-593.

[10] Chakraborty D, Muller R P, Dasgupta S, et al. Mechanism for unimolecular decomposition of HMX (1,3,5,7-tetranitro-1,3,5,7-tetrazocine), an ab initio study[J].TheJournalofPhysicalChemistryA, 2001, 105(8): 1302-1314.

[11] Manaa M R, Fried L E, Melius C F, et al. Decomposition of HMX at extreme conditions: a molecular dynamics simulation[J].TheJournalofPhysicalChemistryA, 2002, 106(39): 9024-9029.

[12] Sharia O, Kuklja M M. Rapid materials degradation induced by surfaces and voids: ab initio modeling of β-octatetramethylene tetranitramine[J].JournaloftheAmericanChemicalSociety, 2012,134(28): 11815-11820.

[13] ZHOU Ting-ting, HUANG Feng-lei. Effects of defects on thermal decomposition of HMX via ReaxFF molecular dynamics simulations[J].TheJournalofPhysicalChemistryB, 2010,115(2): 278-287.

[14] DUAN Xiao-hui, LI Wen-peng, PEI Chong-hua, et al. Molecular dynamics simulations of void defects in the energetic material HMX[J].JournalofMolecularModeling, 2013, 19(9): 3893-3899.

[15] Sharia O, Tsyshevsky R, Kuklja M M. Surface-accelerated decomposition ofδ-HMX[J].TheJournalofPhysicalChemistryLetters,2013, 4(5): 730-734.

[16] Choi C S, Boutin H P. A study of the crystal structure ofβ-cyclotetramethene tetranitramine by neutron diffraction[J].ActaCrystallographicaSectionB:StructuralCrystallographyandCrystalChemistry, 1970, 26(9): 1235-1240.

[17] PENG Chun-yang, Schlegel H B.CombiningsynchronoustransitandQuasi-Newtonmethodstofindtransitionstates[J].IsraelJournalofChemistry, 1993, 33(4): 449-454.

[18] PENG Chun-yang, Ayala P Y, Schlegel H B, et al. Using redundant internal coordinates to optimize equilibrium geometries and transition states[J].JournalofComputationalChemistry, 1996,(17): 49-56.

[19] Gaussian 03: Revision B.03. Gaussian, Inc.: Pittsburgh, PA. 2003.

[20] SUN Hai. An ab initio force-field optimized for condensed-phase applications overview with details on alkane and benzene compounds[J].TheJournalofPhysicalChemistryB, 1998,102(38): 7338-7364.

[21] DUAN Xiao-hui, WEI Chun-xue, PEI Chong-hua, et al. A molecular dynamics simulation of solvent effects on the crystal morphology of HMX[J].JournalofHazardousMaterials, 2010,174(1): 75-180.

[22] XIAO Ji-jun, WANG Wen-rui, CHEN Jun, et al. Study on the relations of sensitivity with energy properties for HMX and HMX-based PBXs by molecular dynamics simulation[J].PhysicaB:CondensedMatter, 2012, 407(17): 3504-3509.

[23] XIAO Ji-jun, LI Song-yuan, CHEN Jun, et al. Molecular dynamics study on the correlation between structure and sensitivity for defective RDX crystals and their PBXs[J].JournalofMolecularModeling, 2013, 19(2): 803-809.

[24] CUI Hong-ling, JI Guang-fu, CHEN Xiang-rong, et al. Phase transitions and mechanical properties of octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine in different crystal phases by molecular dynamics simulation[J].JournalofChemical&EngineeringData, 2010, 55(9): 3121-3129.

[25] Cady H H, Smith L C. Studies on the polymorphs of HMX. Los Alamos Scientific Laboratory Report [R], LAMS-2652 TID-4500, Los Alamos National Laboratory, Los Alamos, NM, 1962.

[26] Choi C S, Boutin H P. A study of the crystal structure ofβ-cyclotetramethylene tetranitramine by neutron diffraction[J].ActaCrystallographicaSectionB:StructuralCrystallographyandCrystalChemistry, 1970,26(9): 1235-1240.

[27] Ewald P P. Evaluation of optical and electrostatic lattice potentials[J].AnnPhys, 1921,64: 253-287.

[28] Rappe A K, Goddard W A, Charge equilibration for molecular dynamics simulations[J].TheJournalofPhysicalChemistry, 1991,95(8): 3358-3363.

[29] Materials Studio 3.0, Accelrys Inc. San Diego, CA, 2004.

[30] Smith G D, Bharadwaj R K. Quantum chemistry based force field for simulations of HMX[J].TheJournalofPhysicalChemistryB, 1999,103(18): 3570-3575.

[31] Rosen J M, Dickinson C. Vapor pressures and heats of sublimation of some high-melting organic explosives[J].JournalofChemicalandEngineeringData, 1969,14(1): 120-124.

[32] Taylor J W, Crookes R J. Vapour pressure and enthalpy of sublimation of 1,3,5,7-tetranitro-1,3,5,7-tetra-azacyclo-octane (HMX)[J].JournalofTheChemicalSociety,FaradayTransactions1:PhysicalChemistryinCondensedPhases, 1976, 72: 723-729.

[33] Boyd S, Murray J S, Politzer P. Molecular dynamics characterization of void defects in crystalline (1,3,5-trinitro-1,3,5-triazacyclohexane)[J].TheJournalofChemicalPhysics, 2009,131(20): 204903.