三自由度含间隙碰撞振动系统Poincaré映射Hopf-Hopf交互分岔的反控制

徐慧东, 文桂林, 伍 新, 张思进,3

(1.太原理工大学力学学院， 山西 太原 030024； 2.湖南大学汽车车身先进设计制造国家重点实验室， 湖南 长沙 410082；3.湖南大学机械与运载工程学院， 湖南 长沙 410082；4.湖南大学特种装备先进设计技术与仿真教育部重点实验室， 湖南 长沙 410082)

三自由度含间隙碰撞振动系统Poincaré映射Hopf-Hopf交互分岔的反控制

徐慧东1, 文桂林2,3,4, 伍 新2, 张思进2,3

(1.太原理工大学力学学院， 山西 太原 030024； 2.湖南大学汽车车身先进设计制造国家重点实验室， 湖南 长沙 410082；3.湖南大学机械与运载工程学院， 湖南 长沙 410082；4.湖南大学特种装备先进设计技术与仿真教育部重点实验室， 湖南 长沙 410082)

对一类含间隙碰撞振动系统Poincaré映射的Hopf-Hopf交互分岔进行了反控制研究。首先，基于碰撞振动系统建立了六维Poincaré映射，由于六维映射相应雅克比矩阵的特征值没有解析的表达式，这使得由特征值特性描述的传统临界分岔准则在确定控制增益中具有很大的局限性。针对这个局限性，建立了包含特征值分布条件、横截条件和非共振条件的显式临界准则。所建立的准则与传统的分岔准则等价，但并不依赖雅克比矩阵特征值的直接计算。然后，针对碰撞的不连续特性导致的隐式Poincaré映射在闭环系统控制设计中的困难，发展了一种基于原碰撞系统的线性反馈控制方法。最后，数值分析给出了在指定的参数点所设计的映射Hopf-Hopf交互分岔的环面解，进一步验证了理论分析的正确性。

非线性振动； Hopf-Hopf交互分岔； 映射的临界准则； 分岔的反控制； 碰撞振动系统

引 言

碰撞振动在实际工程领域中普遍存在。由于碰撞振动系统的不连续性，使其能够展示出丰富且复杂的动力学行为。许多研究者对碰撞系统的分岔和混沌现象作了深入而广泛的研究。Shaw和Holmes[1]用中心流形理论分析了一类单侧约束简谐激力下单自由度振子周期运动的局部分岔，并通过同宿相截条件讨论了混沌运动；文献[2-3]系统研究了碰撞振动系统在非共振和强共振下的Hopf分岔；文献[4-5]研究了两自由度碰撞系统相应Jacobi矩阵有两个-1特征值时的余维二分岔；文献[6]研究了高维映射的Hopf-flip分岔并将理论结果应用于一类两自由度碰撞振动系统中；文献[7-8]研究了一类碰撞振动系统的Hopf-Hopf分岔和不变环面的存在性。文献[9]研究了一类具有对称刚性约束的三自由度碰撞振动系统对称周期n-2运动的音叉分岔、Hopf分岔和Hopf-Hopf分岔。大多数碰撞振动问题的共同特点是碰撞振动系统的维数高，动力响应复杂。为达到预期的工作目的，取得优化的工作效果，大量工程实际问题迫切需要人们对碰撞振动系统的动态行为有更深入、更全面的认识。

Hopf-Hopf交互分岔作为一种典型的环面分岔现象，其特征值分布条件的特点是在两参数的临界分岔点要求有两对复共轭特征值同时位于单位圆周上，这使得此类环面分岔现象具有更加复杂而丰富的动力学行为。Hopf-Hopf交互分岔反控制是在指定的参数位置通过控制使系统生成具有所期望分岔特性的Hopf-Hopf交互分岔解。在实施分岔的反控制时，需要按分岔的临界准则反求出控制增益参数进而通过调控增益参数来生成所期望的分岔解。值得注意的是，传统的Hopf-Hopf交互分岔临界准则是以特征值的特性来描述的，而高维系统的特征值一般又无法解析表示。由此，以往Hopf-Hopf交互分岔的研究通常是通过参数逐点取值的数值方法去试算Jacobi矩阵的特征值及其特性是否满足分岔临界准则，这使得传统的Hopf-Hopf交互分岔临界准则在主动控制分析中具有很大局限性。所以，针对这个局限性很有必要建立一种不依赖于特征值计算的新的Hopf-Hopf交互分岔临界准则。

本文基于一类三自由度含间隙碰撞振动系统建立的六维Poincaré映射，建立了相应映射与传统Hopf-Hopf交互分岔等价的显式临界准则。所建立的准则是由雅克比矩阵的元素组成的一些不等式和等式构成的显式条件，并不依赖于雅克比矩阵特征值的计算，这克服了传统分岔准则在高维系统中对Hopf-Hopf交互分岔进行主动控制存在的局限性。此外，如果直接对Poincaré映射施加控制，由于碰撞的不连续特性导致的隐式Poincare映射的特点使得很难反求出原系统相应的控制参数，这给闭环系统控制设计中带来很大的困难，针对这个困难，发展了一种基于原碰撞微分系统的线性反馈控制方法。最后，基于建立的显式临界准则，使用线性反馈控制方法在指定的参数点实现了所设计的映射Hopf-Hopf交互分岔的环面解。

1 含间隙碰撞振动系统的周期运动及Poincaré映射

图1是一个含间隙的三自由度振动系统的力学模型。质量为M1,M2,M3的质块分别由刚度为K1,K2,K3的线性弹簧和阻尼系数为C1,C2,C3的线性阻尼器联接于支承，每个质块受简谐激振力Pisin(ΩT+τ)只作水平方向的运动(i=1,2,3)。当质块M2的振幅较小而未与刚性约束A(或C)接触时，系统作简单的线性振动。当M2的振幅增加到与刚性约束A(或C)发生接触碰撞时，系统作非线性的碰撞振动。假设力学模型中的阻尼是Rayleigh型比例阻尼，碰撞过程由碰撞恢复系数R确定。

图1 三自由度含间隙振动系统的力学模型Fig.1 The model of three-degree-of-freedom vibratory system with clearances

这里直接给出无量纲变换后系统的动力学方程。未碰撞阶段，系统的运动微分方程为[10]

(1)

碰撞时刻,质块m2的冲击方程为

在方程(1)和(2)中，“．”表示对无量纲时间t求导数。

令Ψ表示方程(1)的正则模态矩阵，ω1，ω2和ω3表示无碰撞情况下振动系统的固有频率。通过模态叠加法可得到方程(1)的通解如下(i=1,2,3)

(4)

(5)

设定系统一周期运动的条件如下：

(8)

2 反控制碰撞振动系统Poincaré映射的Hopf-Hopf交互分岔

2.1 受控系统及其Poincaré映射

对系统(1)和(2)加线性反馈后的控制系统为

通过适当的变换，可以得到方程(9)的解为

(11)

(12)

(13)

Xk+1=F(μ,ε,Xk)

(14)

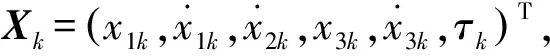
2.2Poincaré映射Hopf-Hopf交互分岔的显式临界准则

首先给出传统的映射Hopf-Hopf交互分岔的临界准则如下：

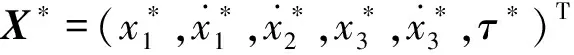
(C1) 特征值分布

(C2) 横截条件

；i=1,2)

这里，分岔参数μ=(μ1,μ2)∈R2。

(C3) 非共振条件

；m=3,4,…)

那么，映射(14)在分岔点μ=μ0处会发生非共振的Hopf-Hopf交互分岔。

定义雅克比矩阵DXF(X*,μ;ε)的特征多项式为

(15)

这里ai=ai(μ,ε)是与分岔参数μ和控制参数ε有关的实数，i=1,…，6。

基于特征多项式(15)的系数，给出Hopf-Hopf交互分岔显式临界准则如下：

命题1：如果映射(14)的雅克比矩阵DXF(X*,μ;ε)的特征多项式(15)在分岔点μ=μ0处满足下面的条件：

(H1) 特征值分布

1+a6>0

(16a)

1-a6>0

(16b)

(16c)

(16d)

1+a1+a2+a3+a4+a5+a6>0

(16e)

1-a1+a2-a3+a4-a5+a6>0

(16f)

(16g)

(16h)

(16i)

(16j)

(H2) 横截条件

(17)

这里，Δ(μ)=

(H3) 非共振条件

cos(2π/m),m=3,4,…

(18)

(Q-1-Q1)2-32(Q-1+Q1)+256≥0

那么，映射(14)在分岔点μ=μ0处会发生非共振的Hopf-Hopf交互分岔。

证明：(i)条件(H1)与条件(C1)的等价性

在证明条件(H1)与条件(C1)的等价性时会用到下面的准则1。设一个四次多项式方程为

P(λ)=λ4+b1λ3+b2λ2+b3λ+b4=0

(19)

准则1：对于四次多项式方程(19)，有两对不同的复共轭特征根同时位于单位圆上当且仅当下面的条件成立：

(a) 由条件(H1)推导出条件(C1)

首先将多项式(15)分解为一个四次多项式和一个二次多项式的乘积

(20)

将多项式(20)展开并与多项式(15)作系数对比有

(21)

然后利用maple软件由条件(H1)中的(16i)和(16j)可以推导出b4-1=0和b1-b3=0两个条件。将b4=1和b3=b1代入表达式(21)中并将简化结果a6=c2代入条件(H1)中的(16a)和(16b)可得|c2|<1，再将简化结果a1=b1+c1，a5=c1+b1c2，a6=c2代入(H1)中的(16c)和(16d)有

(22)

再将特征值λ=1代入多项式(15)和(20)有

(23)

同样将λ=-1代入多项式(15)和(20)有

(24)

基于等式(23)和(24)，由条件(H1)中的(16e)和(16f)并利用推导出的不等式1+c1+c2>0和1-c1+c2>0，容易得到1+b1+b2+b3+b4>0和1-b1+b2-b3+b4>0这两个条件。

(b) 由条件(C1)推导出条件(H1)

(ii) 条件(H2)与条件(C2)的等价性

事实上,在(H2)中的表达式[13]

(25)

式中λi和λj是多项式(15)的根。

对表达式(25)关于参数μi求一次偏导数有

(26)

再对表达式(26)关于μi求一次偏导数，可得表达式(25)关于参数μi的二次偏导数如下

(27)

这里 (·)″表示(·)关于μi的二次偏导数。

(28)

将表达式(28)代入式(27)有

(29)

(30)

(iii) 条件(H3)与条件(C3)的等价性

(31)

将λ=1和λ=-1代入多项式(31)，可得到下面两个方程

(33)

式(33)中还应该保证(Q-1-Q1)2-32(Q-1+Q1)+256≥0。下面来推导Q1和Q-1的表达式。由式(21)简化后的3个表达式a1=b1+c1，a5=c1+b1c2和a6=c2可以解得

(34)

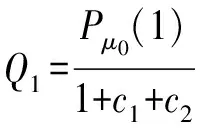
(35)

从命题1中的条件(H1)～(H3)可以看出所建立的准则不依赖雅克比矩阵特征值的计算。在下一节将通过数值算例来验证此准则的有效性。

2.3 数值实验

选取系统的一组参数m2=1.5,m3=1,k2=1,k3=1,f10=0,f20=1,f30=0,δ=0.6,R=0.75，以γ和ω为分岔参数(即,μ=(γ,ω)Τ)。在指定的分岔参数点μ=μ0=(0.004 3,0.45)Τ处，原系统处于稳定的拟周期运动(对应Poincaré映射上的不变圈)，如图2所示。

图2 Poincaré映射上的不变圈Fig.2 The invariant circle on the Poincaré map

图3 控制参数分岔图Fig.3 Control parameter bifurcation diagram

图3中由绿色的细曲线AB，黄色的曲线BC和绿色的粗曲线CD围成的空白区域内，(H1)中所有的不等式(16a)～(16h)都成立，而在灰色区域内至少有(H1)中的一个不等式失败。红色曲线m和蓝色曲线n分别由(H1)中的等式(16j)和(16i)得到。两曲线m和n的两个交点为P1和P2。其中P2点虽然满足等式(16j)和(16i)，但因为此点在灰色区域内并不能保证其他的特征值都位于单位圆内，所以可以确定P1点是合理的控制参数分岔点。此外，青色的曲线l是一条共振曲线，此曲线离分岔点P1比较近，在选取控制参数时应该避开此共振曲线。

在指定的临界分岔点μ=μ0处，通过在控制参数分岔点P1附近选取控制增益v1=0.3和v2=-0.175获得了Poincaré映射上的Hopf-Hopf交互分岔环面解，如图4所示。

图4 在指定的分岔点μ0=(0.004 3,0.45)T处通过控制增益v1=0.3和v2=-0.175得到的Poincaré映射上的Hopf-Hopf交互分岔环面解Fig.4 A torus solution of the created Hopf-Hopf interaction bifurcation on the Poincaré map at μ0=(0.004 3,0.45)T under the control gains v1=0.3 and v2=-0.175

3 结 论

(1)建立了一类高维映射包括特征值分布、横截条件和非共振条件的Hopf-Hopf交互分岔的显式临界准则。此准则是由雅克比矩阵相应的特征多项式的系数表示的一系列等式和不等式组成，不需要直接计算雅克比矩阵的特征值。

(2)在不改变原系统周期运动特性的情况下，发展了一种基于原碰撞微分系统的线性反馈控制方法。

(3)在通过调节控制增益来反控制此类含间隙振动系统映射Hopf-Hopf交互分岔的过程中，相比较传统的映射Hopf-Hopf交互分岔，此准则更加的有效和方便。

(4)基于所建立的准则在指定的参数点实现了三自由度含间隙振动系统Poincaré映射Hopf-Hopf交互分岔的反控制。

[1] Shaw S W, Holmes P J. A periodically forced piecewise linear oscillator[J]. Journal of Sound and Vibration, 1983,90(1):129—155.

[2] Luo G W, Xie J H. Bifurcations and chaos in a system with impacts[J]. Physica D, 2001,148:183—200.

[3] Luo G W, Xie J H. Hopf bifurcations of a two-degree-of-freedom vibro-impact system[J]. Journal of Sound and Vibration, 1998,213(3):391—480.

[4] Xie J H. Codimension two bifurcations and Hopf bifurcations of an impacting vibrating system[J]. Applied Mathematics and Mechanics, 1996,17(1):65—75.

[5] Wen G L. Codimension-2 Hopf bifurcation of a two-degree-of-freedom vibro-impact system[J]. Journal of Sound and Vibration, 2001,242(3):475—485.

[6] Xie J H, Ding W C, Dowell E H, et al. Hopf-flip bifurcation of high dimensional maps and application to vibro-impact systems[J]. Acta Mech. Sinica, 2005,21:402—410.

[7] Xie J H, Ding W C. Hopf-Hopf bifurcation and invariant torusT2of a vibro-impact system[J]. International Journal of Non-Linear Mechanics, 2005,40:531—543.

[8] Ding W C, Xie J H. TorusT2and its routes to chaos of a vibro-impact system[J]. Physics Letters A, 2006,349:324—330.

[9] Yue Y, Xie J H, Xu H D. Symmetry of the Poincaré map and its influence on bifurcations in avibro-impact system[J]. Journal of Sound and Vibration, 2009,323:292—312.

[10]罗冠炜,谢建华.碰撞振动系统的周期运动和分岔[M].北京:科学出版社,2004:118—119.

Luo G W, Xie J H. Periodic Motions and Bifurcations of Vibro-impact Systems[M]. Beijing: China Sciences Press, 2004:118—119.

[11]Iooss G, Los J E. Quasi-genericity of bifurcations to high dimensional invariant tori for maps[J]. Communications in Mathematical Physics, 1988,119:453—500.

[12]Lasalle J P. The Stability and Control of Discrete Processes[M]. Berlin: Springer-Verlag, 1986.

[13]Jury E I, Pavlidis T. Stability and aperiodicity constraints for system design[J]. IEEE Transactions. Circuit Theory, 1963,10:137—141.

Anti-controlling Hopf-Hopf interaction bifurcations on Poincaré map of a three-degree-of-freedom vibro-impact system with clearance

XUHui-dong1,WENGui-lin2,3,4,WUXin2,ZHANGSi-jin2,3

(1. College of Mechanics, Taiyuan University of Technology, Taiyuan 030024, China;2. State Key Laboratory of Advanced Design and Manufacture for Vehicle Body, Hunan University, Changsha 410082, China; 3. College of Mechanical and Vehicle Engineering, Hunan University, Changsha 410082, China; 4. Key Laboratory of Advanced Design and Simulation for Special Equipment, Ministry of Education, Hunan University, Changsha 410082, China)

Anti-controlling Hopf-Hopf interaction bifurcation on Poincaré map in a three-degree-of-freedom vibratory system with clearance is addressed in this paper. Firstly, a six-dimensional Poincaré map of the vibro-impact system is established. As the analytical expressions of all eigenvalues of Jacobi matrix for six-dimensional map are unavailable, the classical critical criteria of Hopf-Hopf interaction bifurcation described by the properties of eigenvalues have a great limitation in obtaining control gains. Aiming at the limitation, a new bifurcation criterion including eigenvalue assignment, transversality condition and non-resonance condition is established. The established criteria are equivalent to the classical critical criteria, but they do not depend on eigenvalue computations of Jacobi matrix. Then, for the difficulty of implicit Poincaré map created by discontinuity of vibro-impact motions in anti-control design of bifurcation of the close-loop system, a linear feedback control method is developed. Finally, numerical simulation shows that a torus solution of Hopf-Hopf interaction bifurcation on Poincaré map is created in a desired parameter location and verifies theoretical analysis.

nonlinear vibration; Hopf-Hopf interaction bifurcation; critical criteria of map; anti-controlling bifurcation; vibro-impact system

2013-12-13；

2014-10-14

国家杰出青年科学基金资助项目(11225212)；国家自然科学基金资助项目(11002052，11372101)

O322; TH113

A

1004-4523(2015)06-0952-08

10.16385/j.cnki.issn.1004-4523.2015.06.013

徐慧东(1978—)，男，博士，讲师。电话：(0731)88821482;E-mail:xhd0931@126.com

文桂林(1970—), 男，教授。电话：(0731)88821482; E-mail: glwen@hnu.edu.cn