长周期地震作用下考虑碰撞效应的偏心隔震结构损伤性能评价
2015-05-10刘文光何文福杨巧荣
刘 阳, 刘文光, 何文福, 杨巧荣
(上海大学土木工程系,上海 200072)
长周期地震作用下考虑碰撞效应的偏心隔震结构损伤性能评价
刘 阳, 刘文光, 何文福, 杨巧荣
(上海大学土木工程系,上海 200072)
由于隔震层位移过大或隔震沟间距设置不当会造成偏心隔震建筑结构与周围挡土墙发生碰撞。合理评估扭转耦合效应及碰撞效应对偏心隔震结构损伤性能的影响具有十分重要的意义。建立了单层偏心隔震结构弹塑性侧扭耦合分析模型,并基于Park-Ang损伤指标定义了上部结构的损伤。以近断层地震和远源长周期地震动作为输入,采用弹塑性时程分析方法对单层单向偏心隔震系统进行损伤性能评价。对相关重要参数进行了地震影响分析。研究结果表明,与设计地震动相比, 在长周期地震作用下考虑碰撞效应的结构损伤值较高,如果间距设置不当甚至会造成结构损伤失效。上部结构及隔震层偏心会对结构损伤产生不利响应。合理设计隔震沟间距可以保证隔震结构在罕遇地震下不出现失效现象。
隔震结构; 长周期地震; 偏心; 碰撞;损伤
引 言
强地震场作用下隔震结构隔震层的变位较大,如果隔震沟(与周围构筑物或建筑物间距)设置不当,易产生碰撞效应甚至引起结构整体倒塌。近年来,国内外学者对隔震结构体系的碰撞效应作了一些研究。Agarwal等(2007)[1]对两幢两层固结建筑和滑移隔震结构间的碰撞效应进行了研究。樊剑等(2007)[2]采用不同碰撞模型分析隔震结构地震响应,并指出不同碰撞模型的计算结果相差在10%以内。Komodromos等(2008)[3]采用不同碰撞模型分析隔震结构地震响应,并对采用缓冲装置的隔震体系进行了分析。叶献国等(2008)[4]针对基础隔震结构和临近构造物发生的碰撞问题进行了计算机三维模拟分析。Matsagar等(2010)[5]选择3条地震波对单层非规则隔震结构进行了扭转碰撞响应分析。Polycarpou等(2010)[6]分别对隔震结构与挡土墙、不同高度的相邻隔震结构之间的碰撞响应进行了研究。黄潇等(2011)[7]采用Kelvin碰撞模型推导了在近断层地震作用下隔震结构与相邻建筑物相碰撞的动力方程,并将隔震建筑与限位装置、与相邻非隔震结构以及与相邻隔震结构在近断层地震作用下相碰撞时的动力响应进行了对比分析。Pant等(2012)[8]采用三维有限元方法对4层钢筋混凝土结构进行碰撞响应的性能评价,指出隔震结构在抵抗剪切失效时显示了很好的性能,由碰撞所引起的结构失效模式一般为弯曲模态。Masroor等(2013)[9]对三层钢框架摩擦摆隔震进行振动台试验研究及数值模拟分析,研究指出碰撞力极大依赖于碰撞间距、冲击速度及挡土墙刚度,碰撞过大时会造成上部结构出现屈服。
本文研究考虑碰撞效应的单层单向偏心隔震结构损伤性能,选取近断层地震和远源长周期地震作为输入分析长周期地震作用下扭转耦合效应及碰撞效应对结构弹塑性地震响应的影响。
1 分析模型
在单向水平地震作用下偏心隔震结构会产生平动和转动,偏心隔震结构示意图如图1所示。在质心处建立坐标系,θs和θb分别为上部结构和隔震层的扭转角,ms和mb分别为上部结构和隔震层的楼层质量,es和eb分别为上部结构和隔震层的偏心距,CRs和CRb分别为上部结构和隔震层的刚度中心。为简化分析作如下基本假定:
(1) 为建立方程简单方便,结构每一层质心和几何中心重合,且质心均处于同一轴上,仅考虑单向刚度偏心;
(2) 由于构件本身的扭转刚度对结构整体响应影响较小,不考虑构件自身的扭转刚度及扭转变形;
(3) 楼板为刚性楼板,不考虑平面外弯曲。
(4) 不考虑桩-土-结构相互作用。
假定(1)是将质心作为参考坐标,而一般的结构上下各层质量分布相似,所以假定(1)是合理的。对于构件自身的扭转刚度对于结构整体抗扭而言作用较小,可以忽略不计,假定(2)也是合理的。对于梁式楼板在水平地震作用下竖向变形较小,可以近似为刚片,假定(3)是合理的。隔震结构对于场地和基础要求较高,边界近似为固结条件,因此分析时忽略掉桩-土-结构相互作用。
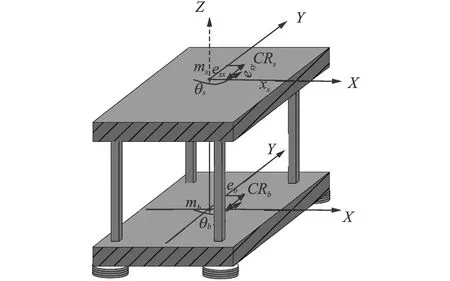
图1 单层偏心隔震结构数学模型Fig.1 Mathematical model of a single-story eccentric isolated structure
1.1 碰撞模型
工程结构在爆炸荷载或强地震作用下引起的冲击碰撞问题较为复杂,一般碰撞过程中伴随材质裂变损伤、能量耗散与转换、侵蚀等复杂物理现象,属于强非线性问题。理论上一般将其处理为动力接触模型,可以采用经典动力学和接触单元法进行求解,因为接触单元法采用接触连接单元模拟接触时的力-变形关系,形式简单易于理解,因此在工程中得到应用。常见的碰撞模型的有:线性弹簧模型、Kelvin模型、Hertz模型及Hertz-damp模型[10-12]。Muthukumar等人的研究表明[10],在取相同参数时不同模型计算的位移和加速度响应差别在12%以内,不考虑能量耗散时(恢复系数e=1.0)会高估体系在地震波作用下的位移和加速度响应均值约为28%和27%。Chau等[11]、Jankowski等[12]较为系统的比较了不同材料碰撞工况下的Kelvin模型、Hertz模型和Hertz-damp模型的数值计算和试验计算结果之间的误差。其计算的结果显示,与试验结果比较而言,线性模型和非线性碰撞模型都能满足工程精度要求, 因此本文选用Kelvin模型模拟隔震层的碰撞受力行为特征。图2给出了碰撞模型示意图。Kelvin模型采用等效阻尼比来考虑碰撞过程中的能量耗散,此时碰撞力Fc为
(1)

(2)
(3)
式中e为恢复系数,m为质量。
1.2 结构层恢复力模型
Bouc-Wen模型已广泛应用于描述强非线性滞回行为的受力对象,其中也包含隔震支座。力学模型如图3所示。隔震层的恢复力关系式如下[13-14]
Fb=αkbxb+(1-αb)Qyzb
(4)
式中αb为隔震层的屈服后刚度比,kb为隔震层的初始刚度,Qy为屈服力,xb为隔震层变形,zb为隔震系统的滞变位移。
其滞变位移zb由如下的表达式确定
(5)
式中xy为屈服位移;Ab,βb,γb和nb为控制滞回位移初始刚度、幅值和滞变形状的参数,调节各个参数可以得到不同的滞回环形状,可根据有关实验来确定这些参数,文中取值分别为1,0.5,0.5及1。
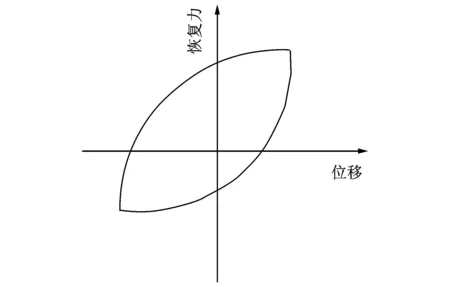
图3 Bouc-Wen模型Fig.3 Bouc-Wen model
建筑结构在强震作用下层间的恢复力-位移滞回曲线通常具有明显的强度退化、刚度退化、捏拢效应以及应变硬化等滞回特性,经典的Bouc-Wen模型经改进后可以反映这些特征[15]。文中采用近似双线性的Bouc-Wen模型模拟,其恢复力及滞变位移如下式
Fs=αsksxs+(1-αs)ksxsyzs
(6)
式中αs为上部结构楼层的屈服后刚度比,ks为上部结构楼层的初始刚度,xs为上部结构楼层的变形,zs为上部结构的滞变位移。
(7)
式中xsy为屈服位移;As,βs,γs和ns为控制滞回位移初始刚度、幅值和滞变形状的参数,文中取值为1,0.5,0.5和1。
上部结构体系的累积滞回耗能ε表达式如下
(8)
1.3 上部结构损伤指数
对地震作用下结构损伤指数一般基于结构的地震反应进行计算,地震反应参数主要有力、变形和能量耗散。本文的研究主要是综合考虑结构最大层间位移响应和塑性累积损伤,因此上部结构损伤指数采用Park-Ang损伤模型[16]
(9)
式中xmax和xd为上部结构楼层最大变形及变形限值,fy为上部结构楼层的屈服力,δE为循环加载对累积损伤程度的影响系数,文中取0.15。损伤指数计算一般介于0~1之间,0代表无损伤状态,1代表损伤破坏失效状态,如果计算得到的值大于1则取值为1。
表1 不同性能水准下损伤指数范围[16]
Tab.1 Damage index ranges for different performance levels[16]

性能水准损伤程度损伤指数范围I:运行安全可以忽略0~0.1II:直接居住轻微损伤0.1~0.2III:损伤控制中等损伤0.2~0.5IV:生命安全严重损伤0.5~0.8V:防止倒塌濒临倒塌0.8~1.0建筑损失倒塌>1.0
1.4 考虑碰撞效应的单向偏心动力方程
考虑隔震层与四周挡土墙之间的碰撞效应,因此体系为双边碰撞体系,由于假定各层结构在Y向存在偏心,上部结构及隔震层的偏心距分别为es和eb,因此在X向地震作用下以X向碰撞为主要分析对象。隔震层与周围挡土墙结构模型如图4所示。CS和CM分别为系统的刚心和质心,gx和gy分别为X向和Y向的碰撞间距。
为了分析方便,仅考虑单向碰撞,间距为gp。假定上部结构相对于基础的平动位移为xs,上部结构平面相对于基础的平面转动角位移为θs,隔震层相对于固定基础的平动位移为xb,相对于固定基础的角位移为θb,从而根据平衡条件建立单向偏心隔震层动力方程。依据力的平衡条件有
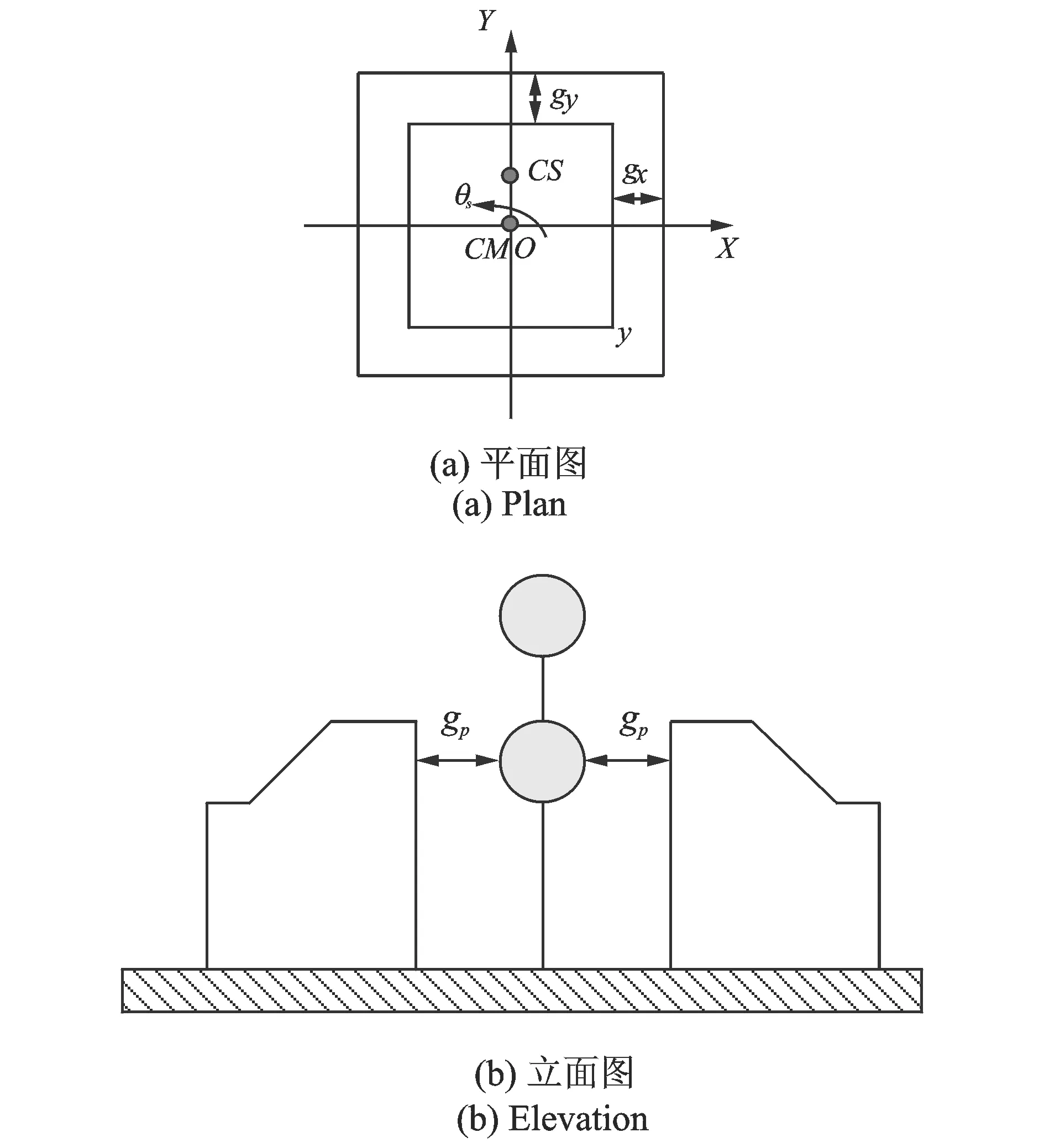
图4 单向偏心隔震层与挡土墙示意图 Fig.4 Schematic diagram of single-direnction eccentric isolated structure and retaining wall
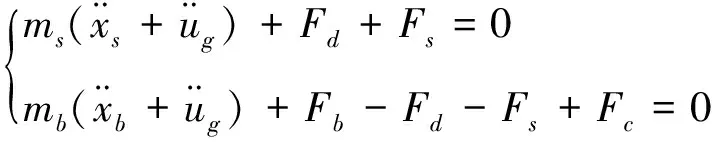
(10)
依据X-Y平面内扭转平衡有
(11)
式中ms,mb为上部结构及隔震层质量;r为回转半径;Fd为上部结构阻尼力,文中取线性粘滞阻尼;Fc和Fcθ分别为碰撞力及碰撞力矩;Fs和Fb为上部结构及隔震层的非线性恢复力;Fsθ和Fbθ为上部结构及隔震层恢复力矩。
上部结构及隔震层恢复力矩表达如下:
Fsθ=Fses
(12)
Fsb=Fbeb
(13)
考虑侧扭耦合效应时隔震层边缘支座位移d为
d=xb+rθb
(14)
式中xb,θb分别为隔震层的平动位移角位移。
当隔震层边缘支座处结构与挡土墙接触时,两者产生碰撞效应,因此隔震层与四周边缘的挡土墙碰撞的条件如下
(15)
由于隔震结构的碰撞问题属于强非线性问题,动力方程没有解析解,可将式(10)和(11)变换为状态方程并采用数值解法求解。
2 长周期地震记录选取
长周期地震动一般特指卓越周期从几秒到几十秒的地震动。从震源机制及历史地震记录来看,长周期地震动可划分为远源长周期地震动和近断层脉冲型长周期地震动。其中大俯冲带(消减带)地震或地壳地震时,在距离震源较远的沉积盆地易产生远源长周期地震动,成因主要与地震波的传播路径(效应)有关,且面波的持续时间一般也较长;近断层地震动震源机制与远源长周期地震动震源机制不同,其具有方向性效应和永久地面位移效应[17]。近断层地震动卓越周期和持续时间(近断层地震卓越周期一般为2~3 s且一般持续10~20 s、远源长周期地震卓越周期一般可达1~10 s及以上,而持时则可达1 min以上)与远场长周期地震相比都较小,为此将近断层地震长周期和远源地震长周期分开考虑以研究长周期地震动设计参数。
目前各国规范尚无统一选择地震动的标准,为了反映强震记录的地震波的统计特性,基于台站和地震信息收集的地震波集需要对地震动真实记录进行选择[18]。本文选择的地震波数据源于美国太平洋地震工程中心PEER/NGA地震波数据库、美国工程强震记录数据中心(CESMD, http://www.strongmotioncenter.org/)及日本防灾科学技术研究所(NIED)。为消除基线漂移现象,对加速度记录进行了校正。为便于考虑场地因素对地震响应的影响,按场地类别对地震波进行划分,但因为各国规范对场地界定标准不一,因此在选择时只能确保与中国大陆抗震规范的场地近似。本文选择地震波时,场地类别与中国大陆抗震规范对应的I~III类。其中近断层地震选波(Near-fault long period ground motions,简记为NF)原则为[19]: (1) 矩震级6.0
为了合理评价长周期地震动的特征,可采用绝对加速度谱、拟速度反应谱(或傅里叶谱)或能量谱进行分析[20]。图5为典型长周期地震动的速度谱。

图5 典型长周期地震波记录的速度谱Fig.5 Individual velocity spectra for long period ground motion records
3 数值算例分析
3.1 分析模型的参数选取
单层偏心隔震结构模型的基本参数取值参考文献[21],其中模型结构总重为200 t,结构质量比ms/mb=1,上部结构阻尼比为0.05,固定基础结构的基本周期为0.5 s。隔震后周期(按屈服后刚度计算)为3.0 s,隔震层屈服力系数取0.02,抗震设防条件为:设防烈度为8度,II类场地,设计地震分组为第一组。上部结构极限位移延性系数取6,结构其它参数如表2所示。文中恢复系数e取值为0.65,碰撞刚度为9.35×107N/m,碰撞阻尼比为0.14[12]。
表2 隔震建筑的屈服位移和屈服力[21]
Tab.2 Yield displacements and strength of the seismically isolated building[21]

参数指标上部结构隔震层屈服位移59mm4.5mm屈服力930.75kN39kN
按抗震规范规定[22]选取符合设计反应谱的7条地震动,分别是1940年El Centro NS波(简记为EL)、1952年Taft波(简记为TA)、1974年唐山地震Tianjin波(简记为TJ)、1968年Hachiheno波(简记为HA)、新疆喀什KS地震波及2条人工波。然后进行时程分析并取7条地震波的平均值,7条地震波的反应谱如图6所示。

图6 地震波记录的加速度反应谱Fig.6 Individual acceleration spectra for a set of ground motion records
3.2 罕遇地震下损伤评价结果
隔震结构的碰撞效应主要由隔震沟间距和碰撞模型参数决定。虽然可以依据规范确定一个隔震沟间距,但是在设计中也有可能存在因为施工不当造成间距过小,因此需要讨论间距gp对结构损伤性能的影响。由于挡土墙等设施对于隔震层位移起到一定限制作用,所以隔震层损伤情况不予考虑。如图7~8所示为(gp=0.1 m) El Centro波(1940 NS)作用下碰撞力时程及加速度时程, 由图可知在发生碰撞瞬间会产生较大碰撞力及瞬间刚度突变现象, 且由此导致上部结构加速度突然放大。图9给出了不同隔震间距下的加速度放大系数(碰撞加速度峰值反应/无碰撞加速度峰值)变化情况,由图可知发生碰撞时加速度放大系数最大可达7.5,反映了碰撞对上部结构加速度造成的不利效应。
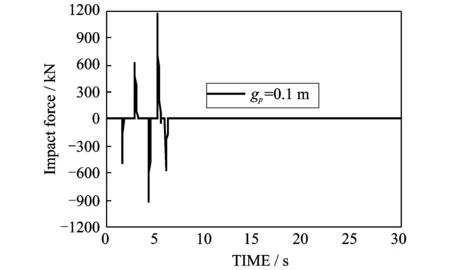
图7 碰撞力时程曲线Fig.7 Impact force time history
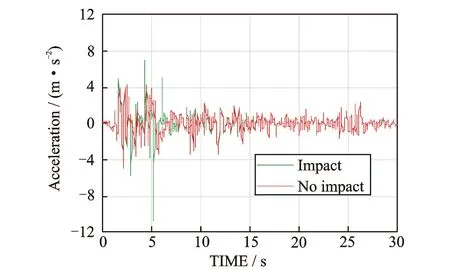
图8 考虑碰撞与不考虑碰撞加速度时程比较Fig.8 Acceleration time history for superstructure of the isolated structure under El Centro wave
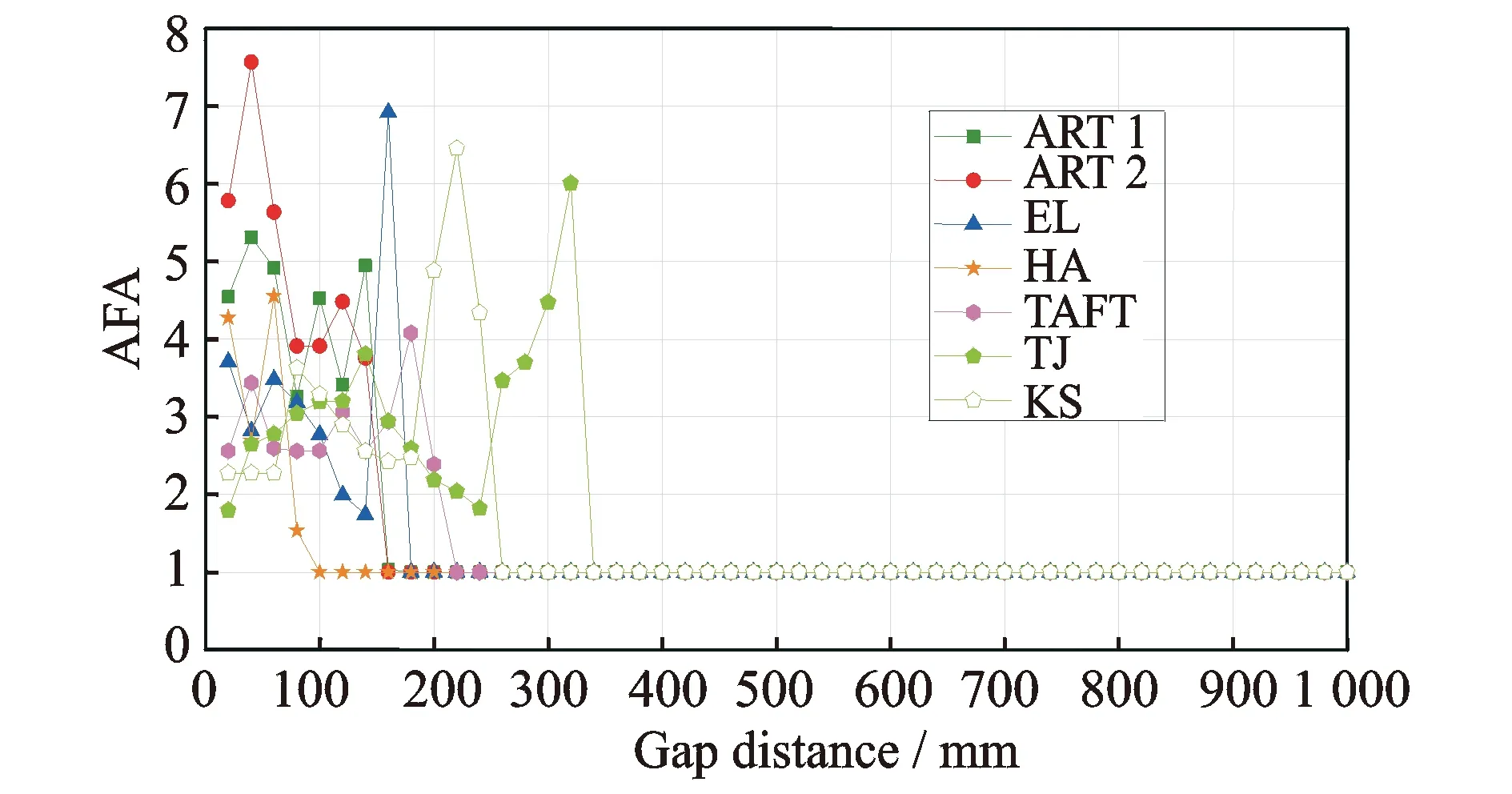
图9 上部结构加速度放大系数Fig.9 Amplification factors of the peak floor accelerations of superstructure
为了考察长周期地震动与设计地震动的差异,选取了7条远源长周期地震和7条近断层地震进行分析(分析结果中进行了编号,分别为1~7,8~14),地震波信息如表3和4所示。本文比较分析时采用时程分析的均值作为参数变化特征的衡量指标。
图10,11为设计地震动、远源及近断层长周期地震动作用下不同隔震沟间距下上部结构损伤情况。由图可知,在设计间距大于0.3 m情况下最不利设计地震动工况计算得到的上部结构损伤值较小,约为0.20,处于轻微损伤状态,结构还保有一定的安全冗余度,即使在间距较小的情况下结构并没有失效;长周期地震下损伤值总体要高于设计地震动,某些地震波在间距较小的情况下会造成结构失效,分析原因可能是由于碰撞激发的频谱成分多为高频分量,如图12给出了碰撞损伤最大的地震波碰撞前后的加速度反应谱情况,由图可知高频分量地震传递到上部结构引起结构共振造成结构损伤程度更加严重。总体上设计地震动下结构损伤随间距增大而减小,适度增加间距对于降低结构损伤有利。从以上分析也说明考虑长周期地震动的隔震沟间距需求要大于设计地震动,一般约可取2.5倍以上。

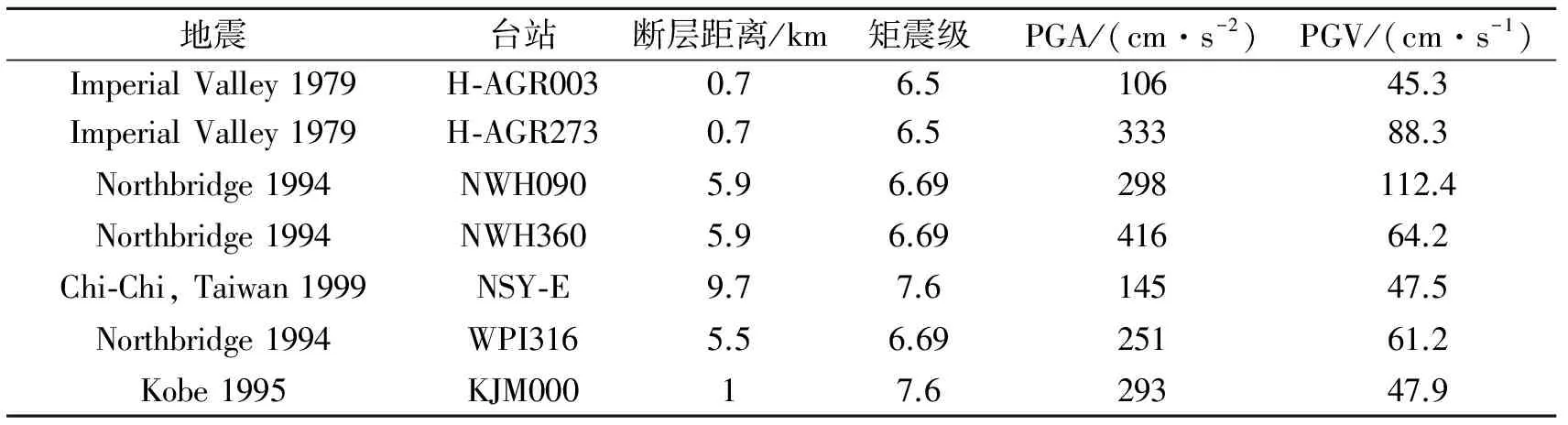
表4 近断层地震动记录
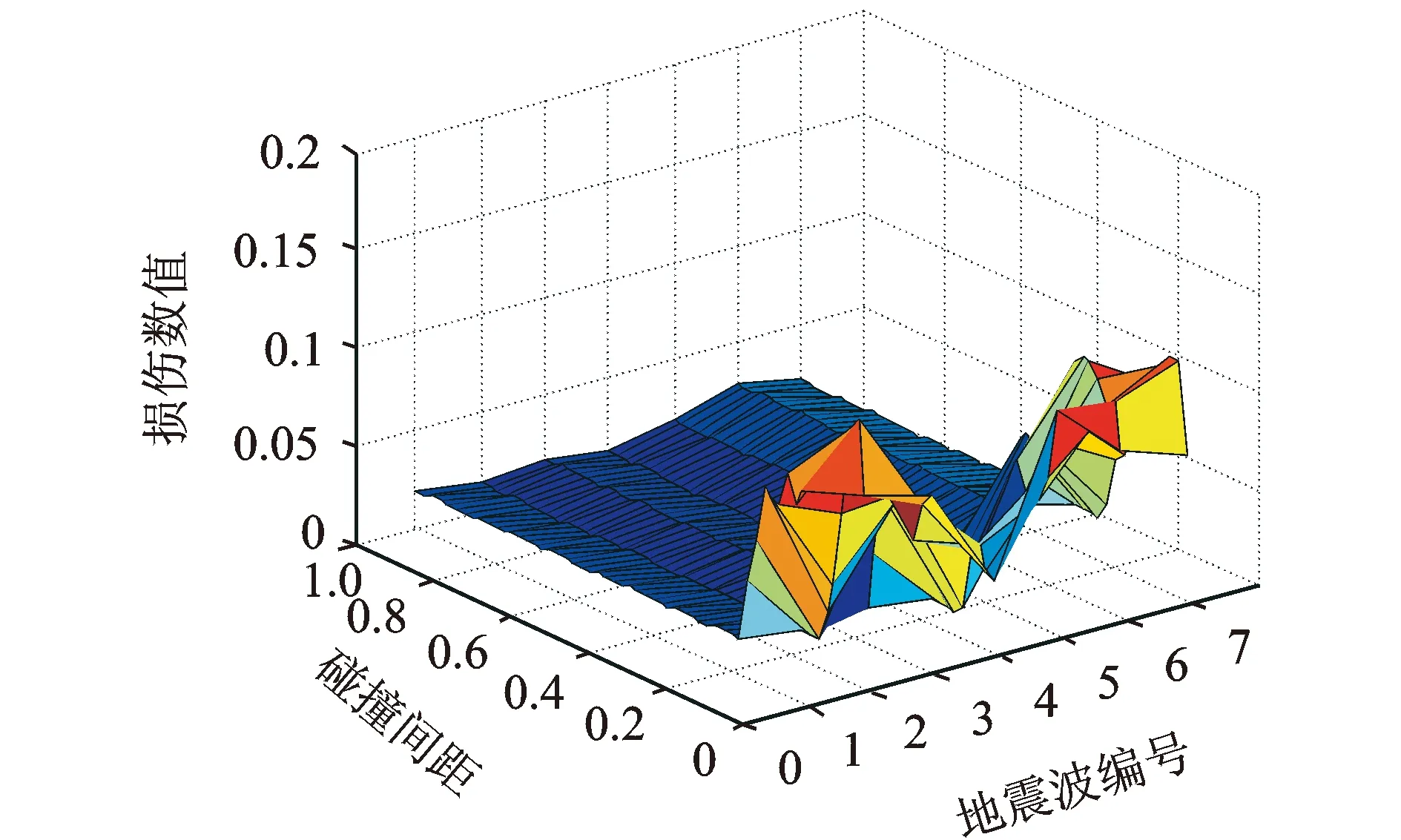
图10 不同碰撞间距下上部结构损伤值(设计地震动,es/r=0,eb/r=0)Fig.10 Damage index values of the superstructure with various gap distances (Design ground motions,es/r=0,eb/r=0)
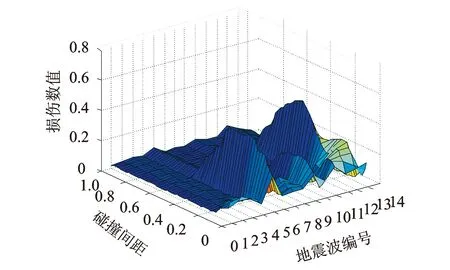
图11 不同碰撞间距下上部结构损伤值(长周期地震动,es/r=0,eb/r=0)Fig.11 Damage index mean values of the superstructure with various gap distances (long-period ground motions, es/r=0,eb/r=0)
隔震结构存在偏心扭转会造成边缘隔震支座的位移放大,因此控制偏心距参数十分重要。本文分析上部结构楼层的偏心率es/r和隔震层的偏心率eb/r对系统的损伤数值的影响。在参数分析中,对于隔震结构体系的偏心率并没有确定的数值范围,Nagarajaiah等[23]对以往的实际工程进行了调查,认为es/r取值范围为[0,0.50]、eb/r取值范围为[0,0.20]可以包含一般工程应用的偏心率取值情况,本文分析给出的范围为[0,1.0]。
图13,14分别为设计地震动与长周期地震动作用作用下不同隔震层偏心距及不同上部结构偏心距时下上部结构损伤情况。图中结果显示结构扭转耦合会给结构碰撞响应及结构损伤带来不利影响。特别对于设计地震动作用时结构损伤随偏心率增加而增加。
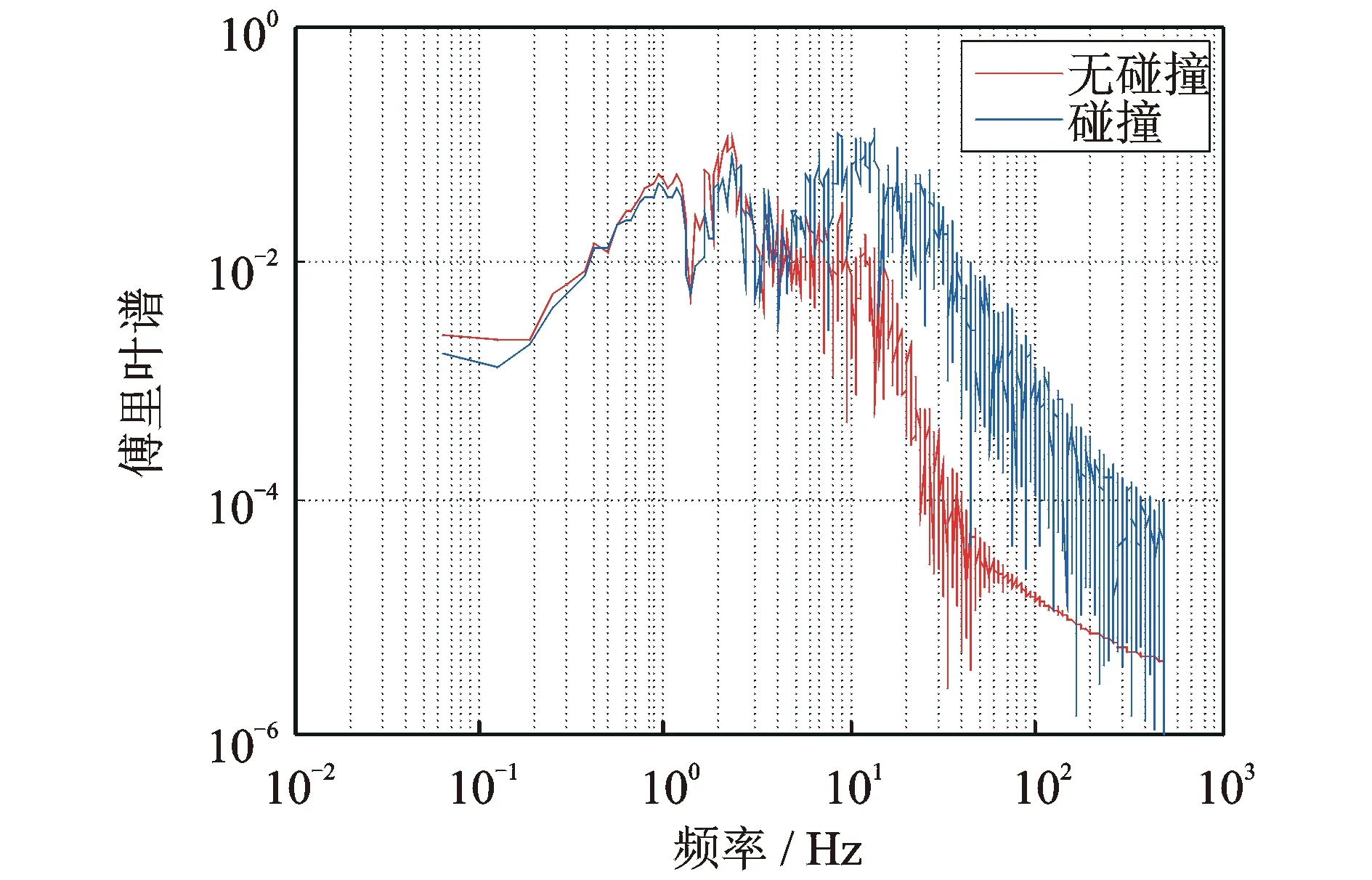
图12 上部结构加速度时程的傅里叶频谱(Montecito Memorial Park360)Fig.12 Fourier spectrum of superstructure acceleration time history(Montecito Memorial Park360)

图13 上部结构偏心率、隔震层偏心率对上部结构损伤的影响(设计地震动,gp=0.1 m)Fig.13 Effect of superstructure and isolation layer eccentricity ratios on superstructure damage index (Design ground motions,gp=0.1 m)

图14 上部结构偏心率、隔震层偏心率对上部结构损伤的影响(长周期地震,Montecito Memorial Park360,gp=0.1 m)Fig.14 Effect of superstructure and isolation layer eccentricity ratios on superstructure damage index ((long-period ground motions ,Montecito Memorial Park360,gp=0.1 m)
4 结 论
本文采用动力弹塑性时程分析方法研究了长周期地震作用下扭转耦合效应及碰撞效应对单层单向偏心隔震结构损伤性能,得到如下结论:
(1) 在设计地震动输入为PGA=0.4g条件下,隔震结构与周边挡土墙的隔震沟间距设置不当会造成上部结构加速度最大可放大7.5倍左右,当间距为0.5 m时上部结构的损伤值约为0.25~0.8。
(2) 长周期地震动及结构偏心会给非对称隔震结构损伤性能带来不利影响。
(3) 在隔震沟间距1 m范围内可以防止结构出现严重损伤甚至失效。
(4) 长周期地震动作用下,当隔震沟间距设置不当所产生的损伤要比设计地震动作用下严重;为避免长周期地震作用的不利影响,应适当增加间距约为常规地震动的2.5倍。
[1] Agarwal V K, Niedzwecki J M. van de Lindt J W. Earthquake induced poundling in friction varying base isolated buildings[J]. Engineering Strucutres, 2007, 29(11): 2 825—2 832.
[2] 樊剑, 刘铁, 魏俊杰. 近断层地震下摩擦型隔震结构与限位装置碰撞反应及防护研究[J]. 土木工程学报, 2007, 40(5):10—16.
Fan Jian, Liu Tie,Wei Junjie. Response and protection of the impact of base friction-isolated structures and displacement-constraint devices under near-fault earthquakes[J]. China Civil Engineering Journal, 2007,40(2):10—16.
[3] Komodromos P. Simulation of the earthquake-induced pounding of seismically isolated buildings[J].Computers and Structures, 2008, 86(7-8): 618—626.
[4] 叶献国, 谢一可, 李康宁. 基础隔震结构在侧向碰撞下的地震反应分析[J]. 地震工程与工程振动, 2008, 28(4):161—167.
Ye Xianguo, Xie Yike, Li Kangning. Earthquake response analysis of base-isolated structure considering side impact [J]. Journal of Earthquake Engineering and Engineering Vibration, 2008, 28(4): 161—167.
[5] Matsagar V A, Jangid R S. Impact response of tosionally coupled base-isolated structures[J]. Journal of Vibration and Control, 2010, 16(11): 1 623—1 649.
[6] Polycarpou P C, Komodromos P. Earthquake-induced poundings of a seismically isolated building with adjacent structures[J]. Engineering Structures, 2010, 32(7): 1 937—1 951.
[7] 黄潇, 朱宏平. 近断层地震作用下相邻隔震结构的碰撞研究[J]. 土木工程与管理学报, 2011, 28(3):249—253.
Huang Xiao, Zhu Hong-ping. Study on impact of adjacent base-isolated structure under near-fault earthquake[J]. Journal of Civil Engineering and Management, 2011, 28(3):249—253.
[8] Pant D R, Wijeyewickrema A C. Structural performance of a base-isolated reinforced concrete building subjected to seismic pounding[J]. Earthquake Engineering and Structural Dynamics, 2012, 41(12):1 709—1 716.
[9] Masroor A, Mosqueda G. Impact model for simulation of base isolated buildings impacting flexible moat walls[J]. Earthquake Engineering and Structural Dynamics, 2013, 42(3): 357—376.
[10]Muthukumar S, Desroches R. Evaluation of impact models for seismic pounding[A].Proceedings of the 13th World Conference on Earthquake Engineering[C]. Vancouver, Canada. 2004.
[11]Chau K T, Wei X X, Guo X, et al. Experimental and theoretical simulation of seismic pounding between two adjacent structures[J]. Earthquake Engineering and Structural dynamics, 2003, 32(4): 537—554.
[12]Jankowski R. Nonlinear viscoelastic modeling of earthquake-induced structural pounding[J]. Earthquake Engng. Struct. Dyn., 2005, 34(6): 595—611.
[13]Wen Y K. Approximate method for nonlinear random vibration[J]. Journal of the Engineering Mechanics Division, 1975, 101(4):389—401.
[14]Wen Y K. Method for random vibration of hysteretic systems[J]. Journal of the Engineering Mechanics Division, 1976, 102(2):249—263.
[15]Goda K, Hong H P, Lee C S. Probabilistic characteristics of seismic ductility demand of SDOF systems with bouc-wen hysteretic behavior[J]. Journal of Earthquake Engineering, 2009, 13(5): 600—622.
[16]Park Y J, Ang A H S. Mechanistic seismic damage model for reinforced concrete[J]. Journal of Structural Engineering, 1985, 111(4): 722—739.
[17]Koketsu K, Miyake H. A seismological overview of long-period ground motion[J]. Journal of Seismology, 2008, 12(2): 133—143.
[18]Katsanos E I, Sextos A G, Manolis G D. Selection of earthquake ground motion records: A state-of-the-art review from a structural engineering perspective[J]. Soil Dynamics and Earthquake Engineering, 2010, 30(4): 157—169.
[19]Alavi B. Behaviore of moment-resisting frame structures subjected to near-fault ground motions[J]. Earthquake Engineering and Structural Dynamics, 2004, 33(6): 687—706.
[20]Takewaki I, Murakami S, Fujita K, et al. The 2011 off the Pacific coast of Tohoku earthquake and response of high-rise buildings under long-period ground motions[J]. Soil Dynamics and Earthquake Engineering, 2011, 31(11): 1 511—1 528.
[22]GB 50011-2010 建筑抗震设计规范[S].北京建筑工业出版社,2010.
GB 50011-2010 Code for seismic design of buildings[S]. Beijing China Architecture & Building Press 2010.
[23]Nagarajaiah S, Reinhorn A M, Constantinou M C. Torsion in base-isolated structures with elastomeric isolation systems[J]. Journal of Structural Engineering, 1993, 119(10): 2 932—2 951.
Damage performance evaluation of eccentric isolated structure system considering impact under long-period ground motions
LIUYang,LIUWen-guang,HEWen-fu,YANGQiao-rong
(Department of Civil Engineering, Shanghai University, Shanghai 200072, China)
Too large isolation layer displacements or inadequate isolation ditch distances will lead to seismic impact between eccentric isolated structure and the surrounding retaining wall. It is very significant to reasonably assess the effect of lateral-torsion coupling and impact on damage performance of the isolated structure. For this problem, the lateral-torsion coupling analysis model for single-direction eccentric isolated structure is established. Based on Park-Ang damage model, superstructure damage index was defined. Damage performance for the single story single-direction eccentric isolated structure under near-fault and far-source long-period ground motions is evaluated by using elastic-plastic time history analysis. The effects of key parameters on seismic responses for the isolated structure were investigated. It is concluded that damage index values for the isolated structure under long-period ground motions are higher than basic design ground motions, and the structure will failure if the isolation ditch distances are improperly set . The lateral-torsion coupling for the isolated structure had adverse effect on the superstructure damage. Designing a proper isolation ditch distance can protect the structure from failure with the rare seismic case.
isolated structure; long-period ground motion; eccentricity; impact; damage
2013-09-17;
2015-07-21
国家自然科学基金资助项目(51278291, 51308331);上海市自然科学基金资助项目(15ZR1416200)
TU352.11
A
1004-4523(2015)06-0910-08
10.16385/j.cnki.issn.1004-4523.2015.06.008
刘阳(1985-),男,博士研究生。 E-mail: winner5299@163.com
刘文光(1968-),男,教授,博士生导师。 E-mail: liuwg@aliyun.com
