改进的自适应算法在谐波检测中的应用

周美君，王云亮,2

（1.天津理工大学 自动化学院，天津 300384；2.天津市复杂系统控制理论及应用重点实验室，天津 300384）

0 引言

近年来，由于电力电子技术的高速发展，各种电力电子设备的应用日益广泛，这些非线性负荷在给人们带来巨大便利的同时却给电网造成了严重的污染。谐波治理变得尤为重要，传统的无源滤波器作为一种被动的补偿装置，已经不能满足电网的要求。有源滤波器（active power filter APF）引起能够实时的抑制谐波和补偿无功，克服了无源滤波器的缺点，在谐波治理方面发挥了重大的作用[1]。因为APF的性能在很大程度上依赖于指令电流的实时、准确检测。所以，如何快速，准确的获取谐波电流变得尤为重要。

在多种谐波检测算法中，基于自适应对消原理的自适应谐波检测算法因其计算简单、具有良好的鲁棒性和和自学习能力，能对频率和相位进行精确的跟踪，在近些年得到了广泛的重视[2]。最早的LMS自适应算法是由Widrow和Hoff在1960年提出的。但是传统的定步长LMS算法存在收敛速度和稳态误差之间的矛盾。所以，有很多学者对变步长LMS算法进行了研究。所谓变步长算法就是当权值远离最佳值时，步长较大，随着权值接近最佳值，步长慢慢变小。1992年，Kwong R H等提出Kwong算法，通过均方瞬时误差e2(n)控制步长的更新。1997年，覃景繁，欧阳景正提出了基于Sigmoid函数LMS算法（SVSLMS） ，2001年，高鹰，谢胜利提出了Sigmoid函数的改进算法。2009年，有学者发现神经网络中的的另一种s函数与Sigmoid函数具有相似特性的双曲正切函数也有着与Sigmoid函数作为步长时的优点，因此，提出了以双曲正切函数实现变步长的LMS算法[3]。但是，它也有Sigmoid函数作为变步长时的缺点即用反馈误差来调节步长，只适用于高信噪比情况下。基于此，有文献提出了一种用时间平均估值梯度的自适应滤波算法[4,5]。本文在对这些算法进行研究之后，并且考虑到电网本身所具有低信噪比特性。提出了一种新的基于双曲正切函数的归一化最小均方算法。经过仿真验证，该算法在有效的提高了权值收敛速度的同时，也降低了稳态误差。能够较为准确的提取出所需的电流。

1 基于双曲正切函数的变步长算法

基于双曲正切函数的变步长LMS算法的表达式如式

(1)所示[6]：

式(1)中，α＞0控制着双曲正弦函数的形状，而β＞0控制着该函数的取值范围，式中的h＞0用来改善函数的底部形状，基于双曲正切函数的变步长算法的显著优点是初始收敛速度快，但是稳态误差较大。

2 改进的变步长自适应谐波检测算法

针对双曲正切函数的变步长算法存在的收敛之后稳态误差大的缺点，本文提出了一种新的变步长算法。改进的变步长算法利用误差的均值估计代替误差来控制步长和权值的更新，同时为了使算法适用于大的动态输入范围，引入了归一化算法，增强了算法的鲁棒性。最后，为了进一步的提高收敛速度，引入动量因子。改进的变步长算法如下所示：

式(2)是对误差的均值估计，式中ɣ是遗忘因子，它是用来调整当前信号在对系统的影响中所占的比重。式(3)中β(n)是控制函数的形状的。式(4)是步长更新公式，式(5)、式(6)是改进了的权值迭代公式。

3 改进的自适应谐波检测算法分析

3.1 变步长因子分析

首先来分析收敛条件，为了保证已有系统的稳定性，使得算法能够收敛，我们需要对步长进行限幅。

μ(n)的取值范围如式(10)所示，它的表达式如式(7)所示：

其中，μmax=1/λmax，λmax是参考输入信号自相关矩阵的最大特征值。μmin＞0，是一个较小的正数。μmin的选取应该同时考虑到收敛速度和稳态失调。

3.2 关于参数ɣ、ε、η、α、β、m、k的选取原则

式(2)中ɣ是遗忘因子，它是用来调整当前信号在对系统的影响中所占的比重。一般的0＜ɣ＜1。我们由参考文献可以得出μ的收敛条件如式(7)所示，β是控制函数的取值范围的，由式(4)可知，当0＜β＜1/λmax时，则基于双曲正切函数的变步长算法必定收敛，但是并不是所有满足这个范围的β都能使算法的收敛达到很好的效果，理想的β应该使算法在初始阶段的时候μ(n)较大，而在权值达到最佳时，应该使得μ(n)很小，所以β应该随着误差的变化而变化，固定的β会引起较大的稳态误差。在式(3)中，关于ε、η的取值，为了保证收敛，二者需要满足如下条件0＜ε＜1，η的取值很小，一般可在以小到10×10-5数量级左右。式(3)中，β(n)随着上一时刻的值β(n-1)和误差的均值估计T(n)的变化而变化,避免了因β固定而引起的稳态误差。α＞0 控制函数的形状，α越小，函数底部形状会越平缓。m＞0用来改善函数的底部形状以减小稳态失调。一般情况下，m越大，则函数的底部形状越平缓则能够减小稳态失调。当然，m也不是越大越好，当m增加到一定程度时，也会引起稳态失调，需要通过实验来寻找合适的m值。

最后，为了进一步加快算法的收敛速度，引入动量因子k，其中0＜k＜1。进一步加快权值的收敛速度[8]。

4 算法的抗干扰性分析

我们从以往的文献中已经知道原有的定步长算法存在着稳态误差和收敛速度之间的矛盾，而基于双曲正切函数的变步长算法虽然具有较高的动态跟踪能力，但是由于其用的是系统反馈误差来更新步长，因而容易受到畸变电流中谐波分量的影响,导致收敛精度较低[9]，详细的推导过程这里不再赘述。我们这里重点分析改进的变步长算法的抗干扰性。

4.1 误差均值估计的引入

改进的变步长算法是利用误差的均值估计来控制步长的更新的，所谓的误差的均值估计实际上相当于对原有的反馈误差信号加了一个滑动时间窗，不断的对窗内的数据进行加权均值计算。这里运用误差的均值估计是因为在电网的谐波检测中，稳态电力谐波均值为0，利用误差的均值估计的滤除负载电流中的畸变了的电流分量而得到实际的跟踪误差也即负载电流中的基波分量和通过自适应谐波检测算法检测到的基波电流之差。

4.2 归一化算法的引入

另外，在权值迭代过程中，引入归一化算法，使算法适应大的动态输入范围，在输入信号有大范围动态变化时，依然能保持系统的稳定性。其中分母中的c是一个很小的常数，避免出现使分母为0的情况。

5 仿真验证

为了验证改进算法的准确性，在MATLAB/simulink上搭建模型进行仿真。在本仿真实验中，仿真参数选取如下：定步长选取的为μ=0.005，基于双曲正切函数的变步长算法中，α=30，β=3×10-3，h=100，改进的变步长算法中，ɣ=0.99，ε=0.95，η=3×10-6，α=30，h=100，k=0.3。

首先合成待检测电流，其包含成分如表1所示，用下面五组数据来进行试验说明。数据如表1所示、检测的结果如表2所示。

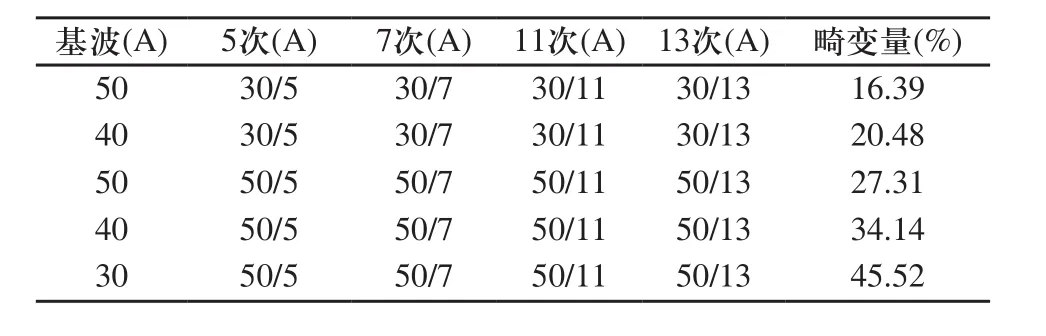
表1 待检测谐波分量

表2 三种检测算法提取基波有功电流畸变率比较

从表2的仿真数据可以看出，三种谐波检测算法谐波检测的精度虽然都会受到谐波畸变量的干扰。即当谐波畸变量越高，算法检测到的波形精度也会相应的变低。但是同等情况下，改进的变步长算法相较于定步长算法和基于双曲正切函数的变步长算法，改进的变步长算法检测出的基波有功电流的谐波畸变率是最低的，定步长算法次之，而基于双曲正切函数的变步长算法是最差的。

下面以50A的基波有功电流，谐波畸变率为27.31%为例进一步来比较三种不同算法检测出的基波有功电流。来比较三种算法的收敛速度和稳态误差。合成的待检测电流波形如图1所示，其相应的频谱分析图如图2所示。

图1 待检测电流波形

图2 待检测电流的频谱分析图

用三种算法对待检测电流中的基波有功电流进行提取，提取出的基波有功电流如图3所示，其中权值的收敛图如图4所示。之后再对三种算法稳态跟踪后的波形进行FFT分析，其频谱分析图如图5、图6、图7所示。

在图3和图4中，曲线1是传统的定步长LMS算法，曲线2是基于双曲正切函数的变步长算法，曲线3是改进的变步长算法，曲线4是参考曲线，即50A的正弦。

图3 三种算法提取的基波有功电流波形

图4 三种算法的权值收敛速度曲线

图5 传统的定步长LMS算法

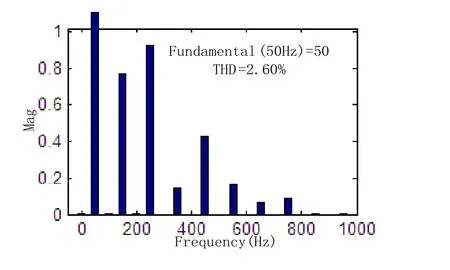
图6 基于双曲正切函数的变步长算法

图7 改进的变步长算法

三种算法先从收敛速度来比较，从图3和图4可以看出改进的谐波检测算法检测到的波形在不到四分之一个周期左右就已经能跟踪参考波形，原始的变步长算法则在一个半周期开始跟踪波形，收敛速度最慢的是定步长算法，在将近3个周期才能跟踪上参考波形。另外从图4中可以看出，曲线3相比1、2来看，不仅收敛速度快，而且收敛之后曲线的波动比较小，因而稳态误差也比较小。曲线2的收敛速度虽然有所增加，但是收敛后的波动范围也是最大的。曲线1收敛后的波动相比于曲线2虽然小了许多，但是它的收敛速度是三者中最慢的。其次从图5、图6、图7的FFT分析图可以进一步的来分析稳态误差，三者提取出的基波有功电流的畸变量分别为：传统的LMS算法为1.32%，而原始的变步长算是三者中最大的，达到了2.60%，而改进的变步长仅为0.42%。

从上面的仿真可以看出，三种谐波检测算法中改进的变步长算法检测出的基波有功电流的谐波畸变率是最低。并且在得到较低的畸变率的同时，还能有最快的收敛速度。

6 结论

基于电网谐波检测速度和准确性两方面考虑，本文在对传统的谐波检测算法进行研究的基础上，提出了一种新的基于双曲正切函数的改进谐波检测算法，该检测算法以误差的均值估计来代替系统误差，以控制步长的更新和权值的迭代，同时为使算法适应大的动态输入范围，在权值的迭代过程中引入了归一化算法。另外，在权值的迭代过程中，引入了动量因子，进一步加快了算法收敛速度。最后，通过仿真验证，该算法在一定程度上有效的解决了系统的收敛速度和稳态误差之间的矛盾。

[1] 曲学基,曲敬凯.电力电子滤波技术及其应用[M].北京:电子工业出版社,2008.

[2] Shiguo Luo,Zhencheng Hou . An adaptive detecting method for harmonic and reactive currents[J].Industrial Electronics,IEEE Transactions on,1995,42(1):85-89.

[3] 杨建宁,陈婕,关佳军,李自成.一种改进变步长的自适应谐波检测算法[J].继电器,2011,39(16):40-44,52.

[4] Ao Wei, Xiang Wanqin，Zhang Youpeng，et al． A new variable step size LMS adaptive filtering algorithm[A].IEEE Conference on Computer science and Electronics E ng ine ering[C],ICCSCE,2009:265-268.

[5] 李建平,蒙建波.基于双曲函数的变步长LMS算法及其分析[J].传感器与微系统,2011,30(5):127-130.

[6] 彭继慎,刘爽,安丽.一种快速收敛的变步长自适应谐波检测算法[J].传感技术学报,2013,26(7):986-990.

[7] 李方伟,张浩.一种新的变步长LMS自适应滤波算法及其仿真[J].重庆邮电大学学报(自然科学版),2009,21(5):591-594.

[8] 包明,王云亮.改进的变步长自适应谐波检测算法[J].电力自动化设备,2011,31(1):71-74.

[9] 付学志,刘忠,李朝旭.Sigmoid函数变步长LMS自适应算法的抗干扰性能改进[J].北京邮电大学学报,2011,34(6):112-115.