具有初始动量的空间机械臂零反作用轨迹跟踪
2015-05-10廖志祥师鹏赵育善郑翰清
廖志祥师鹏赵育善郑翰清
(1北京航空航天大学宇航学院,北京100191)
(2上海航天控制技术研究所,上海200233)
具有初始动量的空间机械臂零反作用轨迹跟踪
廖志祥1师鹏1赵育善1郑翰清2
(1北京航空航天大学宇航学院,北京100191)
(2上海航天控制技术研究所,上海200233)
对具有初始动量的自由漂浮空间机械臂系统进行了研究,考虑其执行在轨任务时便已经具有的动量,根据系统的构型参数建立运动学模型,再采用拉格朗日第二类方程建立动力学模型。利用空间机械臂系统具有冗余自由度这一特性,推导运动学和动力学方程,得到了零反作用运动方程,消除了基座和机械臂之间的角速度耦合作用。末端运动轨迹用多项式插值函数来逼近,根据给定的机械臂末端初始和终止状态来规划其运动轨迹,并将机械臂末端的工作空间转换到关节空间中。根据已知的动力学模型,设计合适的比例-微分(PD)控制率。仿真结果表明,通过选择合适的增益反馈矩阵,机械臂末端能平稳地跟踪目标轨迹,同时,机械臂的运动不会对基座的姿态产生扰动,保证了基座姿态的稳定性及航天器的正常运行。
空间机械臂;轨迹跟踪;零反运动;比例-微分控制;多项式插值;航天器
1 引言
空间机械臂系统由大型航天器基座、若干机械臂杆件和末端抓手三大部分组成[1],在对空间站进行维护和抓捕目标等任务中具有无可比拟的优越性。因此,利用空间机械臂系统代替航天员来完成外太空的各种任务在经济和安全两方面都具有重要意义,并且这将会成为未来发展的必然趋势[2]。
一般而言,当空间机械臂系统执行在轨服务时,为节省燃料,不对基座施加控制;但是,由于外太空的特殊环境,机械臂的运动会对基座产生反作用力和力矩,从而改变基座的位置和姿态,所以需要合理规划机械臂的运动轨迹,保证机械臂沿此轨迹运动时可以实现机械臂与基座的协调运动[3]。另外,基座的姿态对于电源、通信等分系统有着至关重要的作用,国内外很多学者对于如何保证基座的姿态稳定进行了大量研究。文献[4]研究了机械臂末端受到碰撞后,基座和机械臂的协调控制;文献[5]提出了利用循环运动来调整基座姿态的方法,利用机械臂和基座的耦合关系,机械臂沿着特定轨迹循环运动,从而慢慢地调整基座姿态;文献[6]提出了反作用零空间概念,用于处理自由漂浮空间机械臂系统的基座和机械臂的动力学耦合问题。
然而,在这些研究中,机械臂系统在初始时刻都被假定为静止状态,这在实际情况中基本上是不可能出现的。当空间机械臂系统被送至目标轨道并开始正常运行时,整个系统便已经具有了一定量的线速度和角速度。在空间机械臂执行在轨任务之前,不可能也完全没有必要将其运动状态变为静止。因此,实际情况就是空间机械臂系统的线动量和角动量始终都不为零,这也是本文研究的重点和难点。有了初始动量,在运动过程中末端执行器的速度便不能仅用机械臂转动的角速度表示出来,基座的广义速度也不能仅用机械臂转动的角速度表示,还需要考虑初始动量的影响。
2 空间机械臂运动学和动力学建模
空间机械臂系统如图1所示,其中包含n个关节和n+1个刚体,为方便描述,将基座编号为0,机械臂连杆依次编号为1至n,末端用e表示,各向量和矩阵均在惯性坐标系中表示。对本文所涉及的变量和符号说明如下:CM为空间机械臂系统的质心,ri为机械臂第i根连杆质心的位置矢量, r0为基座质心的位置矢量,re为机械臂末端的位置矢量,pi为关节i的位置矢量,rg为空间机械臂系统质心的位置矢量,vi为机械臂第i根连杆质心的速度,v0为基座质心的速度,ωi为机械臂第i根连杆的角速度,ω0为基座的角速度,ki为第i根连杆旋转轴方向的单位矢量,M为系统的总质量,θ=[θ1, θ2,…,θn]T为机械臂各关节角变量,mi为机械臂第i根连杆的质量,I0为基座相对于其质心的转动惯量,Ii为第i根连杆相对于其质心的转动惯量,定义矩阵~r为向量r的叉乘斜对称矩阵[7]。

图1 空间机械臂系统Fig.1 Space manipulator system
由图1中机械臂的构型可以很容易得到机械臂末端执行器的广义速度表达式:

式中 Jb是与基座相关联的雅可比矩阵;Jm是与机械臂相关联的雅可比矩阵,且E表示三阶单位阵,其具体表达式为

系统的线动量P为

角动量L为

对于处于自由漂浮模式的空间机械臂系统,可以认定其动量在运动过程中始终保持不变,若初始线动量和角动量分别为P0和L0,其动量守恒方程为

本文采用拉格朗日方程对空间机械臂系统进行动力学建模。首先令˙xb=v0ω[ ]0T,求得系统的动能(由于空间机械臂系统处于自由漂浮状态,可忽略系统所受万有引力,因此势能为零),将系统的动能代入到拉格朗日方程中,得到
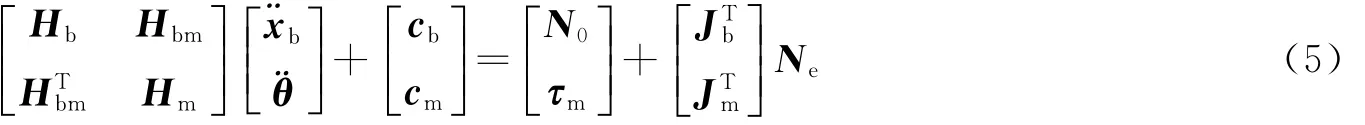
式中 Hb为基座的惯量矩阵;Hbm为基座与机械臂的耦合惯量矩阵;Hm为机械臂的惯量矩阵; cb、cm为非线性项;N0为基座受到的外力F0和外力矩T0,且有N0=[F0T0]T;τm为机械臂关节的驱动力矩;Ne为机械臂末端受到的外力Fe和外力矩Te,且有Ne=[FeTe]T。
3 具有非零初始动量的空间机械臂零反作用运动
在对空间机械臂系统零反作用运动研究中,一般都设定系统的初始动量为零,当机械臂执行任务时,只需要保持基座的角速度始终为零即可,既简化了理论推导过程,也使得控制变得更加容易[8]。然而,这样的设定与实际情况是不相符的,本文提出一种更加接近于实际情况的设定,即空间机械臂系统在执行在轨任务之前,便已经具有了非零的初始动量,因此,为保持基座的姿态运动不受机械臂运动的影响,在机械臂运动过程中,就要保证基座的角速度始终不变且为初始状态。本文定义的零反作用运动指的是使基座姿态运动始终不受影响的机械臂运动,在末端执行器接近目标轨迹的过程中,以及抓捕目标完成后系统的稳定等方面,零反运动都有着重大作用[9]。
由式(4)中的线动量守恒方程可以解出:

将v0的表达式带入到式(4)的角动量守恒方程中:
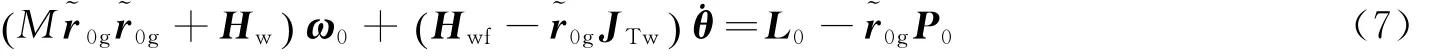
化简为

其中

可以证明,矩阵Hs是非奇异的,因而解得基座角速度的表达式为

进一步求得基座质心的线速度为

其中

那么机械臂末端执行器的速度

其中
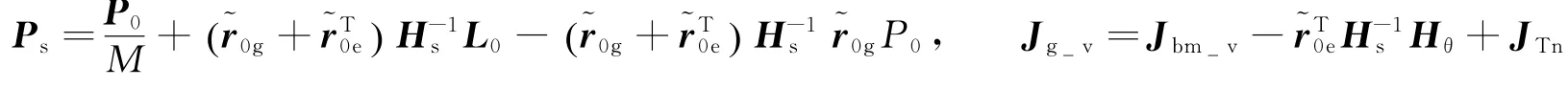
从式(11)与Ps、Jg_v的表达式中可以清楚看到,当初始动量不为零时,末端执行器的速度不仅与关节角运动相关,还与初始动量和雅可比矩阵相关。
为保证机械臂的运动不对基座姿态运动产生扰动,即基座的角速度始终保持初始值不变,机械臂转动的角速度应满足

式中 ω0(t0)为基座的初始角速度。因此,空间机械臂系统的零反作用轨迹跟踪方程为

当机械臂转动的角速度满足式(13)时,机械臂末端执行器既能跟踪任务空间中的期望轨迹,同时,机械臂的运动不会对基座姿态运动产生任何扰动,使基座始终保持期望的姿态角速度。
4 基于逆运动学的轨迹规划
空间机械臂系统所处环境的特殊性决定了其运动的特殊性,可以证明其动量矩守恒方程不可积分。基于这一特点,推导出其运动受非完整约束,这样轨迹规划问题可以简化为:根据已知的初始和终止状态,确定一条使系统从初始状态运动到终止状态的轨迹[10-11]。由式(13)可知机械臂末端执行器工作空间中的轨迹与构型空间中的轨迹之间的关系,因此,只需要获得末端位置的运动规律,并以此为约束条件,就能将末端工作空间运动规律转化为构型空间的运动规律。
本文所研究的重点在于机械臂末端执行器的位置,对其姿态不加要求。机械臂末端执行器的运动状态是时间的函数,因此,可以采用多项式插值的方法来逼近末端位置的状态。考虑到速度和加速度的要求,并让运动轨迹尽量平滑,不至于出现速度级的突变,将机械臂末端执行器的位置状态函数设为

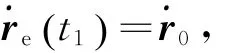
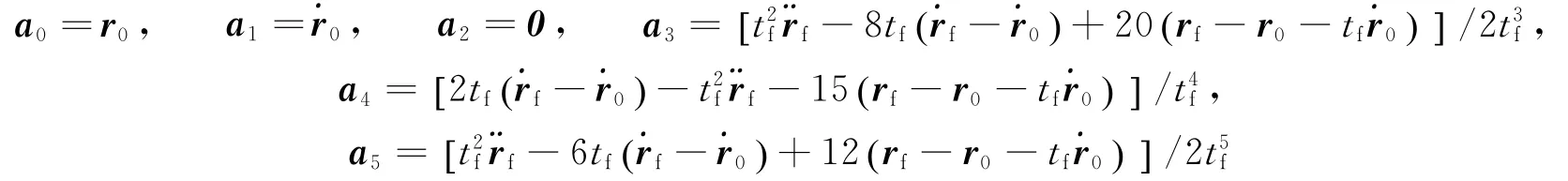
5 已知模型的比例-微分(PD)控制器设计
为了节省燃料,在非必要的情况下,空间机械臂系统不会对基座位置进行主动控制,在抓捕目标物体之前,机械臂末端执行器也没有受到外力作用,所以N0=Ne=0[12]。则系统的动力学方程可写成如下欠驱动形式

消去方程中¨xb变量,并将方程变形得到

在得到新的动力学方程之后,本文采用基于已知模型的PD控制方法

其中u为控制输入,对于指定的期望u,可令

式中 KP为关节角的增益反馈矩阵;KD为关节角速度的增益反馈矩阵;r(t)为参考输入,因此有

式中 θD为机械臂关节角的期望值,设跟踪误差为e=θD-θ且满足

由式(18)和式(19)推导得出控制输入量为

综上各式可以得到基于已知模型的PD控制方案,选择了合适的增益反馈矩阵KP和KD,机械臂末端抓手就能跟踪期望的运动轨迹。
6 仿真分析
为验证可行性,本文以平面三连杆自由漂浮机械臂为模型,基座以及机械臂的物理参数如表1所示。
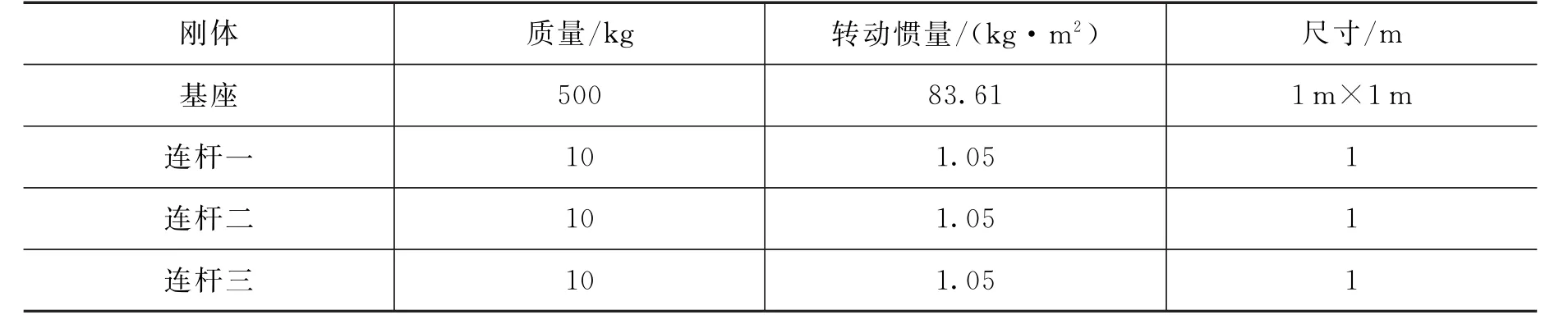
表1 空间机械臂系统惯性参数Tab.1 Inertial parameters of space manipulator system
初始时刻基座质心位置为R0=[0 0]T,姿态角为零,只有横向速度vx和垂直于运动平面的角速度ωz,且vx=0.01 m/s,ωz=0.005 rad/s,各机械臂的初始关节角为θ0=[π/3 -2π/3 π/3]T,机械臂相对于基座为静止状态,即˙θ=0,机械臂末端执行器初始位置为re(t0)=[2.5 0]T。在仿真中,末端执行器跟踪的轨迹为圆,其轨迹方程为

假设经过2.8 s,末端执行器开始与期望轨迹重合。选取合适的增益反馈矩阵,保证控制的精度和误差达到要求,仿真时间为10 s,采样周期为1 ms。
图2为三个关节的实际角速度与期望角速度的对比,可以看出每个关节的实际角速度与期望角速度都非常接近,并且整个运动非常平滑自然,没有出现剧烈震荡的现象,角速度大小也始终保持在可达空间内,没有出现过大的角速度致使机械臂转动太过剧烈,最终无法维持系统稳定的现象。
图3为基座的角速度变化曲线,在整个运动过程中,基座的角速度始终维持在初始值附近,且波动幅度极小,即没有对基座姿态运动产生扰动。图4为机械臂末端的实际轨迹与期望轨迹的对比,机械臂末端执行器首先穿过目标所在的圆轨迹,此时并没有追踪上目标轨迹;在圆轨迹的左上方时,满足位移、速度和加速度一致的条件,这时,末端执行器就追踪上了目标轨迹。可以看出整个运动轨迹非常平滑,末端执行器在到达目标轨迹处后跟踪目标轨迹做圆周运动,从之前的多项式运动过渡到圆周运动非常自然,而且,实际轨迹与期望轨迹的偏差很小,随时间增长逐渐趋近于期望轨迹。图5为基座质心的运动轨迹,初始时刻基座只有x轴正向的速度,由于机械臂和基座之间的耦合作用,在机械臂运动过程中,致使基座产生了y轴方向上的速度,因此,基座质心产生了微小的y轴方向上的位移,并且其运动轨迹呈现一定的周期规律,这与末端执行器跟踪目标轨迹进行圆周运动的周期性一致。
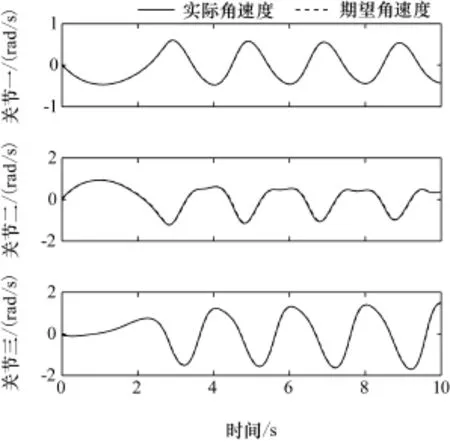
图2 关节一、二、三的实际与期望角速度Fig.2 Actual and desired angular velocity of joint 1,2,and 3
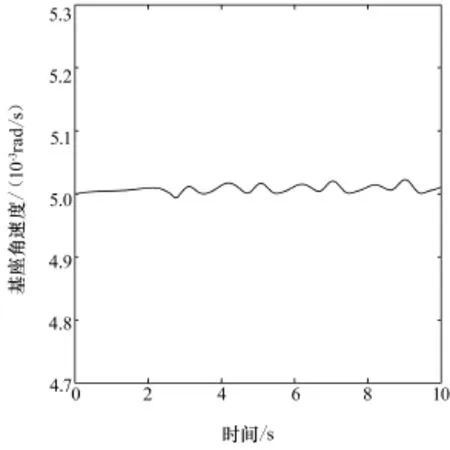
图3 基座角速度变化曲线Fig.3 Angular velocity of the base

图4 机械臂末端运动的期望轨迹与实际轨迹Fig.4 Desired and actual paths of manipulator′s end-effector

图5 基座质心的运动轨迹Fig.5 Trajectory of the base′s centroid
此外,在整个理论推导过程中,对系统的模型没有特殊要求,并没有局限于二维空间中。在实际的编程仿真过程中,为精简计算,令所有刚体只有z轴方向上的角速度,并且其线速度在z轴方向上为零,即在二维平面内求解,但所有的物理量,包括速度、角速度、动量及转动惯量等参数都是在三维空间中表示的,因此本算例同样适用于三维空间的情况。
7 结束语
针对具有初始动量的自由漂浮空间机械臂系统,本文提出的零反作用轨迹跟踪算法既能使机械臂末端执行器平稳跟踪目标轨迹,又能保证基座的姿态稳定性;并且,通过简单实用的PD控制就能实现其功能,为航天器的在轨任务节省了宝贵的燃料资源。在考虑了初始的动量之后,更加符合实际情况,这对航天的在轨维修服务、抓捕失效卫星等任务具有现实意义。由于轨迹规划包含了逆运动学过程,导致在计算过程中可能会有奇异的情况发生,因此,下一步的研究重点,就是在规划机械臂的运动时如何避免奇异。
[1] SATOKO ABIKO,GERD HIRZINGER.Adaptive control for a torque controlled free-floating space robot with kinematic and dynamic model uncertainty[C].The 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems,St.Louis,USA,October 11-15,2009:2359-2364.
[2] 徐文福,詹文法,梁斌,等.自由漂浮空间机器人系统基座姿态调整路径规划方法的研究 [J].机器人, 2006,28(3):291-296.
XU WENFU,ZHAN WENFA,LIANG BIN,et al.Path planning for base attitude adjustment of a free-floating space robot system[J].Robot,2006,28(3):291-296.
[3] 徐栓锋,杨保华,张笃周,等.面向非合作目标抓捕的机械臂轨迹规划方法 [J].中国空间科学技术, 2014,34(4):8-15.
XU SHUANFENG,YANG BAOHUA,ZHANG DUZHOU,et al.Trajectory planning algorithm for manipulators capturing non-cooperative objects[J].Chinese Space Science and Technology,2014,34(4): 8-15.
[4] DRAGOMIR N NENCHEV,KAZUYA YOSHIDA.Impact Analysis and post-impact motion control issues of a free-floating space robot subject to a force impulse[J].IEEE Transactions on Robotics and Automation, 1999,15(3):548-557.
[5] VAFA Z,DUBOWSKY S.On the dynamics of space manipulator using the virtual manipulator with application to path planning[J].Journal of the Astronautical Science,1990,38(4):441-472.
[6] NENCHEV D,UMETANI Y,YOSHIDA K.Analysis of a redundant free-flying spacecraft/manipulator system[J].IEEE Transactions on Robotics and Automation,1992,8(1):1-6.
[7] 王委锋,罗建军,马卫华.自由漂浮空间机器人动力学建模与仿真研究[J].科学技术与工程,2011 11(13): 3004-3008.
WANG WEIFENG,LUO JIANJUN,MA WEIHUA.Study on dynamic modeling and simulation of free-floating space robot[J].Science Technology and Engineering,2011 11(13):3004-3008.
[8] P PIERSIGILLI,I SHARF,A K MISRA.Reactionless capture of a satellite by a two degree-of-freedom manipulator[J].Acta Astronautic,2010,66(5):183-192.
[9] 徐文福.空间机器人目标捕获的路径规划与实验研究[D].哈尔滨:哈尔滨工业大学,2007:60-63.
XU WENFU.Path planning and experiment study of space robot for target capturing[D].Harbin Institute of Technology,2007:60-63.
[10] IOANNIS TORTOPIDIS,EVANGELOS PAPADOULOS.On point-to-point motion planning for underactuated space manipulator systems[J].Robotics and Autonomous Systems,2007,55(7):122-131.
[11] EVANGELOS PAPADOPOULOS,IOANNIS TORTOPIDIS,KOSTAS NANOS.Smooth planning for free-floating space robots using polynomials[C].The 2005 IEEE International Conference on Robotics and Automation,Barcelona,Spain,April,2005:4272-4277.
[12] 洪昭斌.漂浮基空间机械臂冲击动力学建模、控制[C].第32届中国控制会议,中国,西安,2013,7月26—28日:503-506.
HONG ZHANBIN.Modeling of impact dynamics and control for coordinated motion of space manipulator[C]. The 32ndChinese Control Conference,Xi′an,China,July 26-28,2013:503-506.
Zero Reaction Motion Trajectory Tracking for Space Manipulator with Non-zero Initial Momentum
LIAO Zhixiang1SHI Peng1ZHAO Yushan1Zheng Hanqing2
(1 School of Astronautics,Beihang University,Beijing 100191)
(2 Shanghai Aerospace Control Technology Institute,Shanghai 200233)
The free-floating manipulator system with non-zero initial momentum was studied. The configuration parameters of the manipulator system and the Lagrange equations were used to build the dynamic model.In order to eliminate the coupling effects between the base and the manipulators in angular velocity,the zero reaction motion equation was derived by using the manipulator system redundancy.A polynomial interpolation method was used to approach the trajectory of end-effector and the trajectory was planned due to the initial and final position of end-effector which could turn workspace of end-effector into joints space.A suitable proportiondifferentiation(PD)control algorithm was designed to drive manipulators movement.Simulation results demonstrate that the end-effector can smoothly track the target and the movement of the manipulator doesn′t make any disturbance to the base′s attitude at the same time and the spacecraft also can work normally because of the stability of base.
Space manipulator;Trajectory tracking;Zero reaction motion;PD control; Polynomial interpolation;Spacecraft
10.3780/j.issn.1000-758X.2015.05.003
(编辑:车晓玲)
国家自然科学基金(11102007),国家基本科研业务费(YWF-14-YHXY-012)资助项目
2015-04-28。收修改稿日期:2015-07-14
廖志祥 1991年生,2015年获北京航空航天大学飞行器设计与工程专业硕士学位,现为北京航空航天大学飞行器设计与工程专业硕士研究生。研究方向为空间机械臂系统的轨迹规划与动力学控制。
