泥页岩储层可压裂性分析及压裂高度预测方法研究

司马立强, 温丹妮, 闫建平, 谭美琳, 邓浩阳

(1.西南石油大学天然气地质四川省重点实验室, 四川 成都 610500;2.西南石油大学地球科学与技术学院, 四川 成都 610500)

0 引 言

苏北盆地高邮凹陷阜四段泥页岩属于低成熟的热降解生油气阶段,发育页岩油储层;四川盆地自流井组大安寨段热演化程度高,发育页岩气储层[1]。这2个盆地泥页岩储层的基质属低孔隙度低渗透率,储层具有明显的基质孔隙和裂缝双重孔隙特征,需进行压裂改造达到提高产量的目的。

泥页岩储层的可压裂性即储层具有被有效压裂形成压裂缝从而增产的性质[2],是评价页岩储层的重点之一。国外学者多从岩石矿物组分或岩石力学等方面对泥页岩的可压裂性进行了分析。Jarvie等认为脆性矿物含量是页岩脆性的主要因素,以页岩脆性衡量可压裂性[3]。Breyer通过弹性模量、泊松比评价可压裂性[4]。中国很多学者对岩石力学特性、脆性也进行了较深入的研究[5-10]。唐颖等结合国外学者的研究从脆性指数、岩石矿物、岩石力学特性等方面分析泥页岩可压裂性的影响因素,并建立压裂级别[11]。袁俊亮等从脆性指数、断裂韧性、岩石力学特性3个方面分析泥页岩可压裂性[12],但未建立可压裂级别,不能有效指导压裂工作。上述研究均未综合测、录井信息综合评价泥页岩可压裂性[12]。而综合测、录井信息对泥页岩储层进行可压裂性分析更有优势。本文在国内外学者对泥页岩可压裂性研究的基础上,综合测、录井信息,结合岩石力学参数、岩石矿物组分等信息,对泥页岩储层的可压裂级别进行定性、定量评价分析,并建立泥页岩储层压裂高度的预测方法。不仅为页岩油气储层的力学性质研究作参考,并为泥页岩储层完井压裂改造提供有力依据。

图1 A1井岩石力学参数分析图

1 泥页岩可压裂性表征参数分析

弹性模量(E)、泊松比(μ)、脆性系数(IB)、脆性矿物含量(XX)、钻时(TDC)、自然伽马(GR)、密度(DEN)等参数与储层可压裂性密切相关。从图1可见,一般弹性模量偏高、泊松比偏低、脆性系数偏高、脆性矿物含量偏低、钻时偏低值、自然伽马值偏低、密度值偏高的储层可压裂性较好。

(1) 弹性模量E。在线性弹性形变区,应力与应变的比值称为弹性模量[8],在数值上等于弹性体发生单位线应变时弹性体产生的应力大小,是表征页岩脆性的主要岩石力学参数。弹性模量反映了页岩被压裂后保持裂缝的能力,页岩弹性模量越高,脆性越大。

(2) 泊松比μ。泊松比表征弹性材料变形时横向缩短和纵向伸长的比值,也是表征页岩脆性的主要岩石力学参数之一,泊松比反映了页岩在压力下破裂的能力。泊松比越低,脆性越大。如图1所示,苏北盆地阜宁组A1井的3 160.5～3 163 m层段气测结论为泥岩裂缝,测井响应显示为低GR、低AC、高DEN,而E为高值(平均值为23.5 GPa,转化成动弹性模量为61.7 GPa),μ为低值(平均值为0.26)。该段可压裂性较好。

(3) 脆性系数IB。脆性大小除了间接用测井响应和岩石力学参数定性判别外,还可利用岩石力学参数定量计算脆性系数,配合脆性矿物含量可较好地指示泥页岩地层的可压裂性。通常脆性系数[4]越高、脆性矿物含量越高,脆性越大,可压裂性就越好。如图2所示,3 160.5～3 163 m层段气测结论为泥岩裂缝,脆性系数较高(平均值为40.9%),与北美Barnett页岩的脆性系数46.4%接近,灰质含量较高(平均值为35.9%)。可判识该段可压裂性较好。

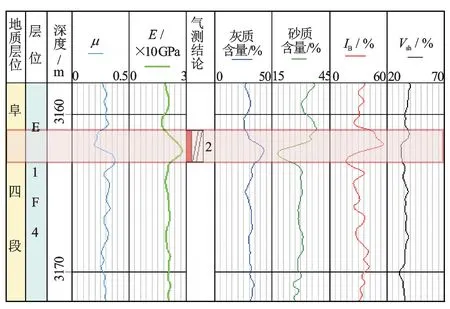
图2 A1井岩石力学参数图

(4) 脆性矿物含量XX。泥页岩脆性的大小对压裂产生的诱导缝的形态有很大影响。脆性矿物含量越高的层段,压裂时越容易形成复杂的裂缝网络,连通泥页岩中的未连通孔隙。脆性含量越高的层段,可压裂性越高。

(5) 钻时TDC。TDC代表钻井过程中在单位储层所花去的时间。有开发价值的层段分为:①无裂缝发育、致密、脆性矿物含量较高的层段,其TDC值较高;②裂缝发育的层段则是高钻时背景下低钻时层段;③裂缝发育的总有机碳含量(TOC)高的泥岩层段,TDC低值。

(6) 自然伽马GR。自然伽马测井曲线测量地层的自然放射性,是识别地层岩性的有效方法之一。储层岩性是影响地层可压裂性的重要参数。如图1所示,该盆地泥页岩储层的岩性可以由GR表征,灰质含量高的层段GR值低,富含有机质的泥页岩层段GR值高。

(7) 密度DEN。与自然伽马相同,密度测井曲线也反映地层岩性,相比于自然伽马测井曲线,它对地层岩性的灵敏度更高。灰质含量高的DEN值高,富含有机质的泥页岩DEN值低。该盆地部分井密度测井曲线明显受到扩径影响,仅在定性分析中考虑其对泥页岩可压裂性的影响。

2 泥页岩可压裂性评价方法

应用IB值、TDC值、TOC值、全烃含量THC值、E值、μ值等参数研究泥页岩储层的可压裂性,综合评价划分泥页岩储层段压裂级别。

2.1 定性评价方法

利用岩石力学参数结合测井响应、脆性系数及脆性矿物含量指标,分析了评价泥页岩可压裂性的适应性,发现识别结果统一。在此基础上,2个盆地的页岩油、页岩气储层提取测井响应值、脆性系数、裂缝发育程度、脆性矿物含量对可压裂级别划分进行了探讨,初步提出了Ⅰ、Ⅱ级划分方案。考虑到不同区块泥岩储层的差异性,分区块进行综合评价(见表1、表2)。

(1) Ⅰ级可压裂层段:这类储层脆性矿物含量高,TDC为高值背景下的低值、TOC高、THC较高,孔隙度较高、E高、μ低、裂缝发育。这类层段有利于压裂。

表1 阜四段泥页岩储层级压裂级别分析表

表2 大安寨段泥岩储层级压裂级别分析表

(2) Ⅱ级可压裂层段:相比于Ⅰ类,这类层段的脆性矿物含量稍低,TDC为高值、TOC稍低、THC稍低,孔隙度稍低、E高、μ低、且裂缝不发育或发育不良好。

由此可知,其脆性系数IB、脆性矿物含量、E值越大,μ、GR值越低,TDC为高值背景下的低值且发育天然裂缝的层段的可压裂性越好。

2.2 综合压裂系数分析法

层次分析法[9-10]是在结合定性和定量分析的基础上,将思维过程层次化、数量化,通过构建各因素之间两两比较矩阵确定各因素权重和最优方案的方法。分析系统各因素之间的关系,建立系统层次结构(见图3)

图3 泥页岩可压裂影响因素层次结构图

(1) 对同一层次的各元素关于上一层中某一元素的重要性进行两两比较,构造两两比较的判断矩阵A(见表3)。

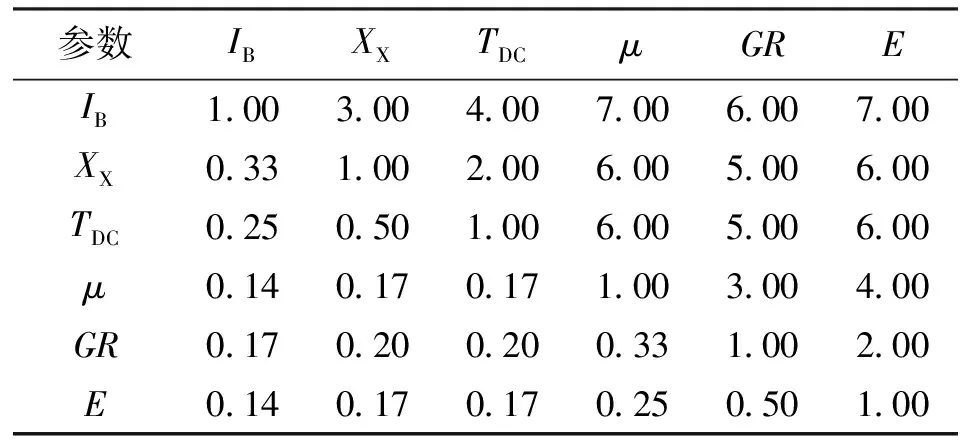
表3 储层压裂级别判断矩阵A

(2) 计算各元素对目标的权重,进而拟合出综合压裂系数ICR

ICR=0.42IB+0.23XX+0.19TDC+0.08μ+

0.05GR+0.03E

(1)

(3) 根据判断矩阵计算的矩阵特征根,对判别矩阵A进行一致性检验,有

IC=(λmax-n)/(n-1)

(2)

ICR=IC/IR

(3)

式中,λmax为最大特征根;IC为一致性指标;IR为随机一致性指标,6阶矩阵IR为1.24。当ICR<0.1时认为判断矩阵具有可接受的不一致性,计算结果IC=0.116,ICR=0.093 58。

(4) 对评价参数进行归一化,E为正向参数

SY=(Emax-E)/(E-Emin)

(4)

μ为负向参数

SP=(μ-μmax)/(μ-μmin)

(5)

式中,SY为正向归一化弹性模量;SP为负向归一化泊松比。当参数为正向参数时,即参数增大时,表明泥页岩的可压裂性好;参数为负向参数,即参数减小时,对泥页岩的可压裂性有贡献。

归一化参数SY分布于0～1之间,归一化参数SP分布于-1～0之间。在参数归一化基础上,根据综合评价系数ICR对大安寨段、阜四段进行研究泥页岩可压裂性分析,得到不同层段的划分标准表(见表4)。

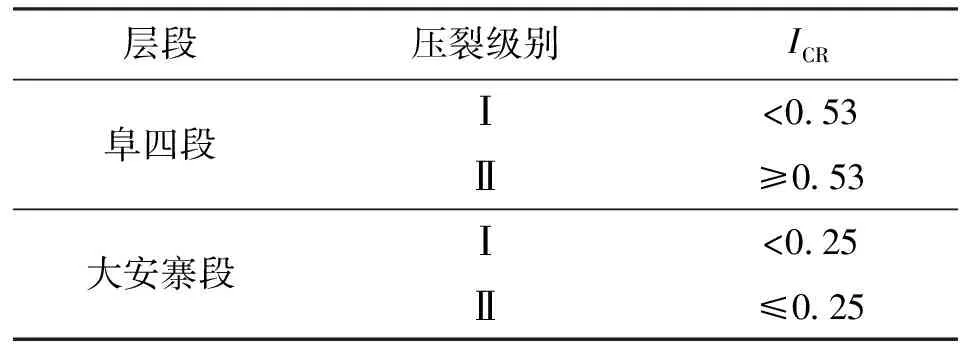
表4 综合压裂级别划分表

2.3 可压裂级别划分

根据建立的可压裂级别分析表,对苏北盆地高邮凹陷A1井阜四段的部分储层(油层)进行可压裂级别分析(见图4),将A1井的1级储层划分为I级压裂层和II级压裂层。Ⅰ级压裂层深度为3 455～3 462.875 m,用A表示裂缝发育,ICR为0.219<0.53;Ⅱ级压裂层深度为3 423.05～3 424.85 m,用B表示裂缝不发育,ICR为0.548>0.53。结果均符合(见表4)综合压裂级别划分表。

根据建立的可压裂级别分析表对四川盆地大安寨段的A2井储层(气层)进行可压裂级别分析(见图5)。Ⅰ级压裂层有2个段,第1段深度为3 839.18～3 843.36 m,ICR为0.117≤0.25,第2段深度为3 864.64～3 867.84 m,ICR为0.130 4≤0.25;Ⅱ级压裂层3段,3 858.92～3 863.32 m,ICR为0.394>0.25,第2段3 870.8～3 874.84 m,ICR为0.289 9>0.25,及3 874.84～3 878.34 m,ICR为0.259 9>0.25。其结果符合(见表4)综合压裂级别划分表,由此可知,可以使用该表来划分储层的可压裂性级别。

图4 A1井可压裂性分析图

图5 A2井可压裂性分析图

3 压裂高度预测

3.1 可压裂高度计算流程与实例分析

在求取岩石力学参数及强度曲线的基础上,建立可压裂高度的计算程序[13-16]。将地层的应力计算转化为顶部应力强度因子Ktop、底部应力强度因子Kbot和岩石韧度KLC。其中,Ktop表示整个射孔段受到的应力在裂缝顶端的作用效应;Kbot表示整个射孔段受到的应力在裂缝底端的作用效应。岩石韧度KLC表示岩石抵抗应力能力强弱。将裂缝高度的计算转化为顶部和底部的应力强度因子计算,与所在处岩石韧度作对比,最后得到裂缝高度。

图6 压裂高度计算程序流程图

按照压裂高度计算程序流程(见图6)计算A1井的压裂高度。A1井储层段(油层)破裂压力为99.1～136.73 MPa,平均值为113.089 MPa,最小水平应力最小值为52.8 MPa,最大值为79.995 MPa,平均值为66.397 5 MPa。设置初始压力为60 MPa,每次增压5 MPa(见图7)。

压裂高度预测的过程中,当压力为60 MPa时,压裂缝分为2个部分3 456.75～3 458 m、3 459.25～3 459.75 m,2个部分压裂缝高度合计2 m;当压力增加至65 MPa时,压裂缝增加2个部分,3 460.5～3 461.625、3 462.375～3 462.875 m,高度合计3.875 m;当压力为70～105 MPa时,3 455～3 462.875 m层段全部压裂成功,压裂缝高达8 m。

3.2 压裂高度实例证明

以四川盆地A2井储层(气层)为例,实际压裂改造工作采用加砂压裂方式,破裂压力150.3 MPa,压裂改造层段3 838～3 878 m,共压裂改造40 m地层, 其试气结论为日产气0.259 2×104m3, 为典型低产气层。依照实验程序,其计算结果与现场实际结果相符,表明该程序计算精度高,可用于泥页岩压裂高度预测。

图7 A1井压裂高度预测图

4 结 论

(1) 综合测、录井信息,分析脆性矿物含量、脆性系数、自然伽马、密度、钻时、泊松比、弹性模量等因素对泥页岩可压裂性的影响,定性分析、评价泥页岩可压裂性;弹性模量越大、泊松比越小、脆性系数越大、脆性矿物含量越高、钻时为高背景之下的低值、自然伽马越低、密度值越大的储层可压裂性越高。

(2) 建立综合压裂级别评价系数ICR定量评价泥页岩储层的可压裂性,建立定量评价标准,评价泥页岩可压裂性。识别结果与定性分析结果识别一致,说明了综合测录井信息可以有效地评价页岩油气储层可压裂性。

(3) 在综合评价泥页岩的可压裂研究基础上建立可压裂高度计算方法,预测压裂高度,从而为泥页岩储层射孔开发工作提供指导,并为页岩油气的研究提供技术支撑。

参考文献:

[1] 柳妮, 林良彪, 陈洪德, 等. 四川盆地川西北地区侏罗系自流井组大安寨段页岩气聚集条件 [J]. 中国地质, 2014, 41(5): 1664-1672.

[2] 闫萍, 孙建孟, 苏远大, 等. 利用测井资料计算新疆迪那气田地应力 [J]. 新疆石油地质, 2006, 27(5): 611-614.

[3] Jarvie D, Hill R J, Ruble T E, et al. Unconventional Shale-gas Systems: The Mississippian Barnett Shale of North-central Texas as One Model for Thermogenic Shale-gas Assessment [J]. AAPG Bulletin, 2007, 91(4): 475-499.

[4] Breyer J A, Alsleben H, Enderlin M B. Predicting Fracability in Shale Reservoirs [C/OL]. [2012-08-10]. http: ∥www.searchanddiscovery.com/abstracts /pdf/2011/hedberg-texas/abstraces/ndx_breyer.pdf.

[5] 杨迪, 刘树根, 单钰铭, 等. 上扬子地区牛蹄塘组黑色页岩的力学性质 [J]. 成都理工大学学报: 自然科学版, 2013, 40(6): 277-287.

[6] 李庆辉, 陈勉, 金衍, 等. 含气页岩破坏模式及力学特性的试验研究 [J]. 岩石力学与工程学报, 2012, 31(增刊2): 3763-3771.

[7] 刁海燕. 泥页岩储层岩石力学特性及脆性评价 [J]. 岩石学报, 2013, 29(9): 3300-3306.

[8] 李庆辉, 陈勉, 金衍, 等. 页岩气储层岩石力学特性及脆性评价 [J]. 石油钻探技术, 2012, 40(4): 18-22.

[9] Saaty T L. The Analytical Hierarchy Process [M]. New York: McGraw-Hill, 1980: 17-62.

[10] 蒋难得, 周兴林, 何雅琴. 基于MATLAB/GUI层次分析法软件实现及其实例应用 [J]. 物流工程与管理, 2012, 34(9): 104-107.

[11] 唐颖, 邢云, 李乐忠, 等. 页岩储层可压裂性影响因素及评价方法 [J]. 地质学前缘, 2012, 19(5): 357-362.

[12] 袁俊亮, 邓金根, 张定宇, 等. 页岩气储层可压裂性评价技术 [J]. 石油学报, 2013, 34(3): 523-527.

[13] 万哲, 章成广, 黄文新. 用测井资料预测压裂缝高度的方法研究 [J]. 测井技术, 2007, 31(5): 479-481.

[14] 胡南, 夏宏泉, 杨双定, 等. 基于Iverson模型的低渗透率油层压裂高度测井预测研究 [J]. 测井技术, 2011, 35(4): 371-375.

[15] 刘红磊, 熊炜, 高应运, 等. 方深1井页岩气藏特大型压裂技术 [J]. 石油钻探技术, 2011, 39(3): 46-52.

[16] 易新民, 唐雪萍, 梁涛, 等. 利用测井资料预测判断水力压裂裂缝高度 [J]. 西南石油大学学报, 2009, 31(5): 21-24.