页岩气层脉冲中子元素测井蒙特卡罗研究

刘军涛, 张锋, 元哲珑, 王新光, 韩飞, 陈铁光

(1.中国石油大学(华东)地球科学与技术学院, 山东 青岛 266580; 2.中国石油大学(华东)CNPC测井重点实验室, 山东 青岛 266580; 3.成都中核高通同位素股份有限公司, 四川 成都 610041)

0 引 言

随着世界油气需求的持续增长与常规油气产量的不断下降,非常规油气储层,如页岩气、页岩油、致密砂岩气储层的勘探与开发,越来越受到人们的重视[1]。评价页岩气藏的潜力主要涉及页岩矿物成分、黏土成熟度、总有机碳含量等方面。基于化学源的元素俘获伽马能谱测井采用单个伽马探测器,记录元素俘获特征伽马射线,当不与自然伽马能谱及Al活化测井一起使用时,通过解谱及氧化物闭合模型处理分析能够确定Si、Ca、S、Fe、Ti、Gd等元素含量,进而分析储层岩性、脆性程度等特性,在页岩气储层评价中发挥了极其重要作用[2-4];James Galford、James Egbe等[5-6]研究了俘获伽马能谱元素解谱及元素含量求取方法,将俘获伽马能谱元素含量计算结果与实验分析结果进行了对比。庞巨丰等[7]研究了适用于某一固定地层的地层元素测井中子-伽马能谱解析理论和方法。国内外关于脉冲中子元素测井在页岩气储层中应用的数值模拟研究,及利用非弹伽马能谱确定低俘获截面元素含量与俘获伽马能谱计算结果对比的研究相对较少。

本文采用蒙特卡罗数值模拟方法建立基于D-T中子源与BGO探测器的元素能谱测井仪器及页岩气储层模型,研究利用俘获伽马能谱及非弹伽马能谱确定元素含量方法,并利用蒙特卡罗模拟方法模拟不同元素俘获及非弹标准伽马能谱,基于形成的标准谱及非弹、俘获伽马能谱确定元素含量方法,处理页岩气储层的伽马响应谱,并对计算结果进行了对比分析。

1 伽马能谱确定地层元素含量理论

1.1 俘获伽马能谱计算元素含量方法

通过脉冲中子源的时序设计,能够采集俘获及非弹伽马能谱,利用伽马能谱确定地层元素含量时,采用最小二乘法进行谱数据处理。假定地层中有m种元素,在整个伽马能谱中选取n个能量道区,ci是测量伽马能谱第i道的计数率[8],则

(1)

式中,aij为测井仪器的响应矩阵元,由m个归一化的标准谱产生;yj为第j种元素非弹或俘获产额;εi为拟合误差;ci为测量伽马能谱第i道相对计数率。

基于目标函数如式(2)所示,采用加权最小二乘法处理计算元素产额如式(3)所示

(2)

Y=(ATWA)-1ATWC

(3)

(4)

设Fc是随深度变化的俘获谱归一化因子,Ycj为元素俘获谱计算产额,Scj为元素的俘获谱探测灵敏度因子,Wcj为利用俘获伽马能谱确定元素质量百分数;则元素产额与元素百分含量的关系为[9]

(5)

利用俘获伽马能谱确定元素含量时,利用骨架所有元素总质量分数为1,但由于俘获谱没有氧及碳元素信息,因此采用地层骨架氧化物闭合模型,计算地层元素含量[8]。

(6)

式中,Xj为氧化物或碳酸盐指数。联合式(5)与式(6)可以计算得到地层元素含量。

1.2 非弹伽马能谱确定元素含量方法

非弹性散射作用明显的元素种类相对较少,且无法区分干骨架及流体中的氧元素含量,不满足骨架氧化物闭合模型的条件,获取非弹归一化因子FI存在困难。考虑有些元素非弹性散射及辐射俘获作用都较为明显如Si、Ca等,利用2种元素含量比值,可以将非弹归一化因子约掉如式(7)所示,进而根据获取的元素非弹灵敏度因子及产额计算元素含量。

(7)

WI,Si=WC,Si

(8)

(9)

(10)

式中,WI,A为非弹谱求取元素A的百分含量,如C、Mg、Al等元素;WC,Si为利用俘获能谱求取元素Si的百分含量;SI,A为元素A的非弹灵敏度因子;SI,Si为元素Si的非弹灵敏度因子。计算得到C元素含量后,扣除方解石、白云石及菱铁矿中无机碳,可以获取储层总有机碳含量。

2 地层元素标准伽马能谱数值模拟

2.1 蒙特卡罗模拟模型

利用MCNP输运程序[10]建立如图1所示计算模型。仪器采用D-T中子源,中子发射能量为14 MeV;探测器为BGO晶体探测器,长度为15 cm,直径为6 cm,能量分辨率为13%。仪器外径为9.5 cm,源距为45 cm;屏蔽体为钨,长度5 cm。井径20 cm,井内流体为淡水,密度为1.0 g/cm3;地层纵向及径向厚度分别为140 cm、60 cm,划分为5 cm×5 cm的栅元;D-T中子源发射脉冲宽度为40 μs,在0～40 μs采集非弹伽马能谱,在50～100 μs采集俘获伽马能谱。

图1 蒙特卡罗模拟模型

2.2 元素标准谱数值模拟

采用上述数值计算模型,模拟过程中采用分布模拟方法,采用了权窗、能量分裂及时间分裂3种减小方差技术,跟踪粒子数为2×109,高伽马计数能道的相对误差平均约为0.03,低伽马计数能道相对误差平均约为0.08。考虑到有利于中子减速及实际地层组成,设置地层组成分别为SiO2、CaCO3、TiO2、Fe2O3、S、H2O等物质[11-12],地层密度分别为2.65、2.71、4.3、5.24、1.96、1.0 g/cm3,模拟得到地层伽马能谱,扣除井眼流体及仪器材料对模拟谱的影响,获取Si、Ca、Ti、Fe、S、H等元素俘获伽马标准能谱如图2所示。改变地层物质组成分别为H2O、Si、Ca、C22H46等物质,地层密度分别为1.0、2.33、1.55、0.8 g/cm3,进行低能中子截断,计算地层非弹伽马能谱,扣除干扰因素影响,得到C、O、Si、Ca等元素非弹伽马标准能谱如图3所示。

图2 部分元素俘获标准伽马能谱

图3 部分元素非弹标准伽马能谱

3 页岩气储层测井响应及计算结果分析

3.1 元素测量灵敏度因子获取

利用图1中所示数值计算模型,建立组成分别为SiO2与CaCO3、SiO2与CaCO3、SiO2与Fe2O3、SiO2与TiO2、SiO2与MgO、SiO2与K2O、SiO2与Na2O、SiO2与S的地层模型。利用模拟得到的元素标准谱,处理计算得到的俘获伽马能谱,计算地层元素产额,根据式(11)计算元素测量相对灵敏度因子;建立Si与Ca、Fe、S、Al、C等元素的混合地层,利用相同的数据处理方法,使用的能谱能量范围为0.7～8.3 MeV,获取地层元素非弹灵敏度因子如表1所示。

(11)

式中,yi为元素j的非弹或俘获产额;Wtj为第j种元素的质量百分含量;ySi为Si元素非弹或俘获产额;Wt,Si为Si元素的质量百分含量。

表1 地层元素灵敏度因子

3.2 页岩气储层元素含量计算结果及分析

根据页岩气储层岩样矿物X射线衍射技术实验分析结果[13-14],按照页岩气储层实际组成,建立由干酪根、孔隙、石英、方解石、绿泥石、伊利石、黄铁矿、钾长石、钠长石、白云石组成的页岩气储层计算模型。设置地层模型体积百分比组成为干酪根(C:76.4%、H:6.3%、O:11.1%、N:4.1%、S:2.1%)2%、石英(SiO2)38%、钾长石(KAlSi3O8)5%、钠长石(NaAlSi3O8)15%、方解石(CaCO3)5%、白云石(CaMg(CO3)2)2%、伊利石(KAl2[(Al,Si)Si3O10](OH)2·4H2O)20%、绿泥石((Mg,Fe,Al)3[(Al,Si)Si4O10](OH)2)5%、黄铁矿(FeS2)3%、孔隙度5%,地层密度为2.465 g/cm3,孔隙度中地层水Cl离子浓度为50 000 mg/L,记录俘获及非弹伽马能谱如图4、图5中红线所示,模拟谱能道计数平均相对误差约为8%。基于模拟计算得到的元素俘获及非弹标准伽马能谱,利用加权最小二乘方法分别处理地层俘获及非弹混合伽马能谱,计算地层元素产额,得到非弹及俘获伽马反演能谱与模拟谱对比如图4及图5所示。

图4 页岩气储层反演俘获谱与记录俘获谱

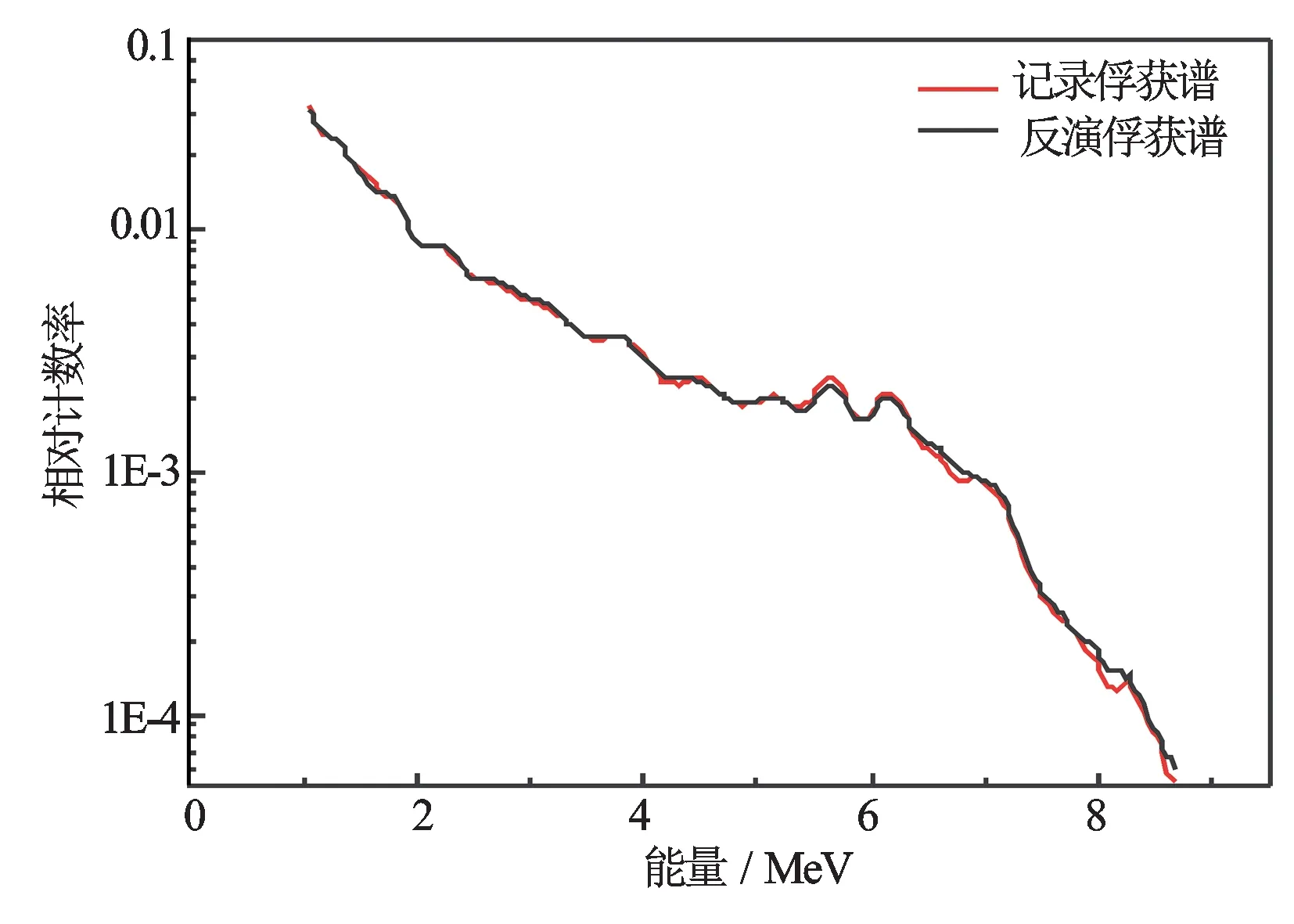
图5 页岩气储层反演非弹谱与记录非弹谱

由图4及图5可以看出,反演计算的非弹及俘获伽马能谱与测量伽马能谱在低计数率部分略有差异,其他能量段吻合性非常好,全谱相关系数都达到0.99,验证了获取的元素非弹与俘获伽马标准谱的准确性。采用氧化物闭合模型处理俘获伽马能谱,没有考虑绿泥石及伊利石中结晶水,计算得到地层骨架元素质量含量如表2所示。根据式(4)计算由于混合谱的蒙特卡罗模拟误差引起元素产额最大相对误差范围为4.66%。

表2 俘获谱元素含量计算结果

由表2可以看出,利用俘获伽马能谱计算地层元素含量与理论值基本吻合,Mg与Na元素的计算误差偏大。主要因为Mg元素具有低热中子俘获截面,Na元素含量较少,计算结果误差偏大;由于C元素具有更低的辐射俘获截面(约为0.003 b),利用俘获伽马能谱基本不能计算地层C元素含量。利用给出的非弹伽马能谱元素含量计算方法,计算地层骨架总有机碳、Mg、Al、Na、S等元素含量与俘获谱计算结果对比如表3所示。

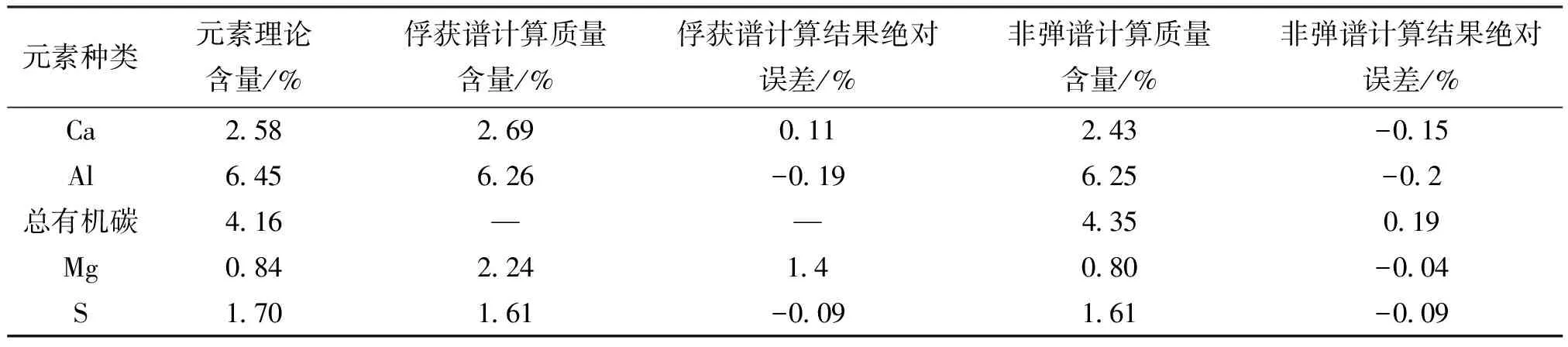
表3 非弹谱元素含量计算结果对比

由表3可以看出,利用非弹谱计算元素含量与理论值具有很好一致性;Ca、Al及S元素含量计算误差与俘获谱计算误差基本相当;Mg元素计算精度明显高于俘获谱计算结果;另外,非弹谱能够准确计算储层总有机碳含量,相对误差小于5%。总有机碳及Mg元素含量的确定,为页岩气储层岩性划分及脆性等有关参数计算提供了重要参考。

4 结 论

(1) 在利用俘获伽马能谱计算元素含量基础上,可以利用元素传递的方法处理非弹伽马能谱,确定页岩气储层总有机碳、Mg等具有低俘获截面元素的含量。

(2) 采用蒙特卡罗模拟方法,计算得到了地层元素非弹及俘获伽马标准能谱;利用给出的非弹伽马能谱元素含量确定方法,计算储层总有机碳、Mg、Al等元素含量,结果与理论值具有很好的一致性;相对利用俘获伽马能谱确定元素含量,非弹谱计算Mg元素含量具有更高精度,且能够准确确定页岩气储层总有机碳含量。

参考文献:

[1] 邹才能, 朱如凯, 吴松涛, 等. 常规与非常规油气聚集类型, 特征, 机理及展望——以中国致密油和致密气为例 [J]. 石油学报, 2012, 33(2): 173-187.

[2] Quirein John, James Witkowsky, Jerome Truax, et al. Integrating Core Data and Wireline Geochemical Data for Formation Evaluation and Characterization of Shale-gas Reservoirs [C]∥SPE Annual Technical Conference and Exhibition, 2010.

[3] Lewis Rick, David Ingraham, Marc Pearcy, et al. New Evaluation Techniques for Gas Shale Reservoirs [C]∥Reservoir Symposium, 2004.

[4] Shim Yen Han, Keith Atwood, Jeffrey Kok, et al. Defining Reservoir Quality for Successful Shale Gas Play Development and Exploitation [C]∥Canadian Unconventional Resources Conference, 2011.

[5] Galford James, John Quirein, Scott Shannon, et al. Field Test Results of a New Neutron Induced Gamma Ray Spectroscopy Geochemical Logging Tool [C]∥SPE Annual Technical Conference and Exhibition, 2009.

[6] James Egbe, Omole O, Jacob Diedjomahor, et al. Calibration of the Elemental Capture Spectroscopy Tool Using the Niger Delta Formation [C]∥Nigeria Annual International Conference and Exhibition, 2007.

[7] 庞巨丰, 李敏. 地层元素测井中中子-伽马能谱解析理论和方法 [J]. 同位素, 2006, 19(2): 70-74.

[8] Grau Ja, Js Schweitzer. Elemental Concentrations from Thermal Neutron Capture Gamma-ray Spectra in Geological Formations [J]. Nuclear Geophysics, 1989(3): 1-9.

[9] Grau Ja, Js Schweitzer, Dv Ellis, et al. A Geological Model for Gammaray Spectroscopy Logging Measurements [J]. Nuclear Geophysics, 1989, 3(4): 351-359.

[10] Briesmeister Judith F. MCNP: A General Monte Carlo N-particle Transport Code [J]. LA-12625, 1993.

[11] Wu Wensheng, Lizhi Xiao, Lijuan Zhang, et al. Calculating Standard Captured γ Spectra of Formation Elements [J]. Petroleum Science, 2012, 9(4): 463-468.

[12] 张锋, 王新光, 侯爽, 等. 脉冲中子地层元素能谱测井方法及数值模拟研究 [C]∥第六届中俄测井国际学术交流会论文集, 2010, 青岛: 133-139.

[13] 陈尚斌, 朱炎铭, 王红岩, 等. 四川盆地南缘下志留统龙马溪组页岩气储层矿物成分特征及意义 [J]. 石油学报, 2011, 32(5): 775-782.

[14] 蒋裕强, 董大忠, 漆麟, 等. 页岩气储层的基本特征及其评价 [J]. 天然气工业, 2010, 30(10): 7-12.