基于偶极横波测井的低渗透砂岩气层识别方法

张海涛, 石玉江, 张鹏, 范宜仁, 杨小明, 李虎

(1.中国石油集团长庆油田分公司勘探开发研究院, 陕西 西安 710018; 2.中国石油大学(华东)地球科学与技术学院, 山东 青岛 266580; 3.中国石油大学(华东)CNPC测井重点实验室, 山东 青岛 266580; 4.中国石油集团长庆油田分公司第一采气厂, 陕西 榆林 718500)

0 引 言

低渗透储层通常是指孔隙度小于15%、渗透率低于50×10-3μm2的碎屑岩储层[1],由于其孔隙度、渗透率等性能非常差,储集空间有限,电阻率和孔隙度测井资料受岩石骨架影响较大,流体对其响应特征贡献小[2]。偶极横波测井与地层电阻率无关,利用偶极横波测井可以获取真实的地层骨架及流体声波速度信息,如纵横波速比、弹性力学参数、频谱信息等,这些声学信息对储层的含气性有一定的敏感性,从Biot-Gassmann理论出发,通过提取与流体有关的项,可以增加气层的敏感程度,可用于判别流体性质。

鄂尔多斯盆地东部横跨伊陕和晋西挠褶带2大构造单元,属典型的低孔隙度低渗透率储层,岩石矿物组分复杂、流体识别较为困难。本文以上古生界二叠系低渗透砂岩储层为研究对象,利用斯伦贝谢公司DSI测井资料,通过弹性模量差比与纵波等效弹性模量差比、纵横波速比与波阻抗以及泊松比、体积压缩系数等弹性力学参数建立了气层识别指标,在此基础上基于Biot-Gasmann理论提取流体因子建立了识别气层的方法。

1 利用偶极横波测井建立气层识别指标

1.1 弹性模量差比与纵波等效弹性模量差比气层识别标准

(1) 弹性模量差比法。储层岩石的弹性模量的计算公式为

(1)

储层完全饱含水时的岩石弹性模量为

(2)

式中,ρb为体积密度,g/cm3;Δtc为纵波时差,μs/m;Δtcw为水层的纵波时差,μs/m;Δts为横波时差,μs/m;Δtsw为水层的横波时差,μs/m。

弹性模量差比定义为

(3)

当储层孔隙中含有天然气时,水层的弹性模量Mw一定大于储层实际的弹性模量M。因此,若ΔM>0则指示为气层,反之则为非气层。

(2) 纵波等效弹性模量差比法。岩石的等效弹性模量为纵波速度与纵波阻抗的乘积。在岩性和孔隙度相近的条件下,气层纵波阻抗与纵波速度均小于水层,因此可利用岩石纵波等效弹性模量识别流体性质[3],其计算公式为

(4)

式中,ρb为体积密度,g/cm3;Δtc为纵波时差,μs/m;P为纵波等效弹性模量,GPa。

储层完全饱含水的等效弹性模量Pw定义为

(5)

式中,ρf为地层水密度,g/cm3;ρma为砂质骨架密度,g/cm3;ρsh为泥岩密度,g/cm3;Δtf为地层水的纵波时差,μs/m;Δtma为砂质骨架声波时差,μs/m;Δtsh为泥岩骨架声波时差,μs/m;Pw为水层纵波等效弹性模量,GPa。

纵波等效弹性模量差比(视弹性模量系数)为

ΔP=(Pw-P)/P

(6)

储层孔隙空间含有天然气时,Pw大于P,因此,当ΔP>0时指示为气层,反之为非气层[4]。纵波等效弹性模量差比法与弹性模量差比法的基本原理类似,但在没有偶极横波测井资料情况下,纵波等效弹性模量差比法同样可以进行气层识别。

1.2 纵横波速比与纵波阻抗气层识别标准

1.3 弹性力学参数气层识别标准

对于低渗透砂岩含气储层,纵横波速度比R变小,其泊松比也会减小。因此,储层含气时会引起弹性力学参数的显著变化,造成泊松比减小、体积压缩系数升高,鉴于这种特性可以将体积压缩系数与泊松比交会对比显示,在气层段会形成明显的镜像包络体,指示为气层,便于利用测井资料进行快速定性评价[5]。泊松比σ与体积压缩系数CB分别为

σ=(0.5R2-1)/(R2-1)

(7)

(8)

2 基于Biot-Gassmann理论的流体因子识别方法

2.1 Biot-Gassmann理论

Biot M A[6]利用饱含流体岩石的拉梅常数,有

λsat=λdry+β2M

(9)

式中,λsat为饱含流体岩石的拉梅常数;λdry为干岩石的拉梅常数;β为Biot系数,表示水的压力为常数的条件下流体体积变化与地层体积变化之比;M为模量,表示在地层体积保持不变的前提下,把流体压入地层所需的压力。

Gassmann[7]从体积模量和剪切模量的角度出发,得出

Ksat=Kdry+β2M

(10)

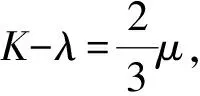
μsat=μdry

(11)

即,剪切模量不受孔隙流体的影响。

式(10)中,Gassmann进一步指出,在低频限制条件下,有

(12)

(13)

式中,Km为岩石基质的体积模量;Kfl为流体的体积模量。将式(12)和式(13)代入式(10)中得到[8]

(14)

式中β2M项可以用于区分干岩石与饱和岩石的不同情况,并且该项并不依赖于式(9)和式(10)的第1项,Murphy等[9]将其定义为孔隙空间模量Kp。因此,利用β2M,可以改写饱含流体岩石的纵波速度方程。

若用Biot方程可得

(15)

若用Gassmann方程可得

(16)

上述公式为等价形式,可以简化为

(17)

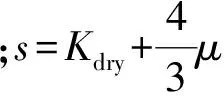
(18)

2.2 流体因子提取方法

根据波阻抗与速度和密度的关系,结合式(17)和式(18),可以得到

纵波阻抗

内向性问题行为指在课堂上不容易被发现，并不影响课堂秩序的课堂问题行为，如上课不认真听讲、走神、发呆等分散注意力的行为，以及多疑、敏感，害怕被提问、烦躁不安等精神问题。相较于外向性行为，内向性问题行为不易被教师察觉，不干扰课堂秩序，具有发现难、矫正难的特点。但这对学生的影响更大，会使其学习效率降低。

(19)

横波阻抗

(20)

根据以上分析,可知ρ×f是与流体有关的项,为了得到这个流体项,需要一个因数c,使得cμ的值等于干岩石的骨架项s。因此,就可以获得这个流体项ρ×f,把它定义为流体因子[10]

(21)

由式(15)和式(16)可知,因数c通常由以下3种方式得到

(22)

求得流体因子ρ×f的关键是准确确定c值,求取方法有很多种,国内外专家学者开展了大量的研究工作,其中之一就是估算干岩石的泊松比σdry

(23)

对于纯砂岩,σdry约为0.1,相应的干岩石的纵横波比约等于1.5,c值为2.25。

鉴于以上分析可知,研究区块不同,因数c也随之不同。因此,要想获得有效流体因子,必须针对研究区的实际情况确定最优的因数c。本文中,从岩石声学实验着手,通过测量75块干岩样和40块饱和水岩样的纵横波速度获得纵横波速比与孔隙度的关系(见图1)。由图1可知,不同孔隙度下的干燥岩样的纵横波速比近似为一个常数1.524,饱和水岩样随着孔隙度增加,纵横波速比逐渐增加。

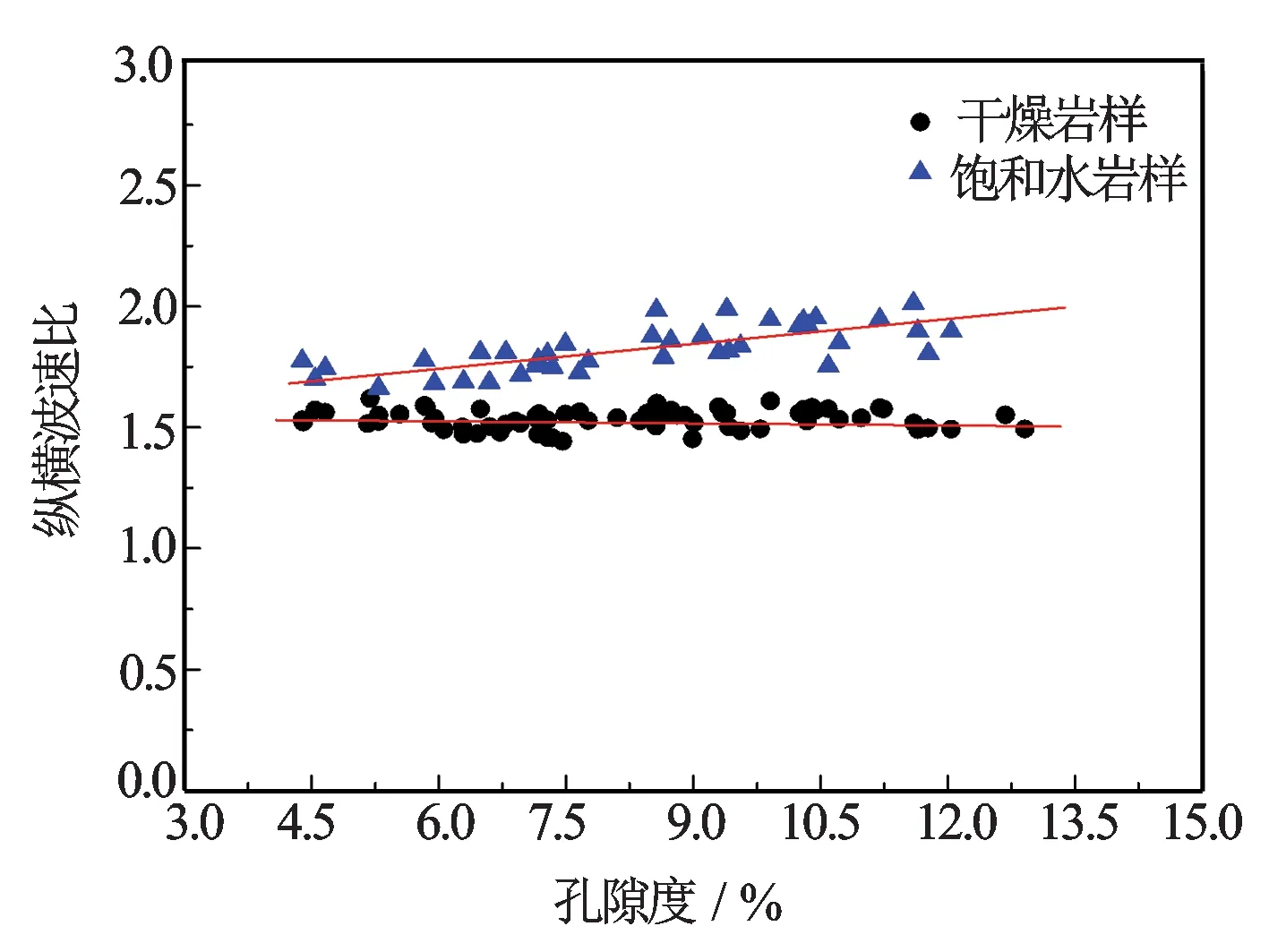
图1 纵横波速度比与孔隙度交会图(干燥岩样与饱和水岩样)

鉴于干岩样的以上特征,对研究区75块岩样的纵横波速比、泊松比等弹性参数取平均值可得弹性参数值(见表1),利用式(22)可得因数c为2.324。

表1 干燥岩样声学实验弹性常数平均值

选取研究区块M1井、M2井的气层段,S1井、M2井的差气层段以及M3井、Y1井的干层段等6个测试层以及泥岩层段分别绘制横波速度与流体因子、泊松比与流体因子交会图(见图2和图3)。可知,研究区气层和干层、差气层和干层界限明显,流体因子小于15时,储层含气; 差气层与气层界限模糊,交叉性较明显,但整体上表现为气层流体因子和泊松比均略小于差气层的特征。

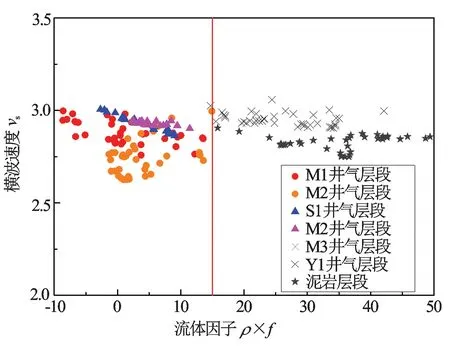
图2 横波速度与流体因子交会图

图3 泊松比与流体因子交会图

3 实际资料应用分析

图4为A井气层识别效果图,分别利用弹性模量差比与纵波等效弹性模量差比法、纵横波速比与纵波阻抗重叠法、泊松比与体积压缩系数交会法以及流体因子识别法对该井段进行处理,从图4可见,在11号气层段弹性模量差比与视弹性模量系数均大于0,纵横波速比与纵波阻抗相反方向刻度后重叠,两者出现明显的包络线镜像特征,泊松比与体积压缩系数交会,表现为泊松比减小,体积压缩系数增大,同样具有明显的包络线镜像特征;流体因子小于背景值15;经生产测试验证,该段储层产量为2.472 9×104m3/d,综合解释为气层,解释结论与生产结论一致。

图4 A井气层识别效果图

同样,利用上述方法对B井进行处理(见图5)。从图5可见,16号储层段弹性模量差比和纵波等效弹性模量差比略大于0,纵横波速比与纵波阻抗相反方向刻度后重叠以及泊松比与体积压缩系数交会图中虽然出现了包络线镜像特征,但不明显,而流体因子小于背景值15,经生产测试验证,该气层段产量为3.400 7×104m3/d,综合解释为气层,解释结论与生产结论一致。因此,基于Biot-Gassmann理论的流体因子识别方法应用效果较好。

图5 B井气层识别效果图

4 结论与认识

(1) 对于低渗透砂岩气藏可以利用偶极横波测井数据进行气层识别,声波信息不受岩石电学性质的影响。弹性模量差比与纵波等效弹性模量差比、纵横波速比、泊松比以及压缩系数均可作为气层识别的指标。

(2) 流体因子识别方法从Biot-Gssmann理论角度入手,通过提取与流体相关的项,建立了识别气层的标准,流体因子小于15时,指示为气层。通过实际资料处理及生产资料验证,证实该方法具有较好的应用效果。

参考文献:

[1] 李道品, 罗迪强, 刘雨芬, 等. 低渗透砂岩油田开发 [M]. 北京: 石油工业出版社, 1997.

[2] 成志刚, 张蕾, 赵建武, 等. 利用岩石声学特性评价致密砂岩储层含气性 [J]. 测井技术, 2013, 37(3): 253-257.

[3] 中国石油勘探与生产分公司. 低孔低渗油气藏测井评价技术及应用 [M]. 北京: 石油工业出版社, 2009.

[4] 胡向阳, 吴健, 陈嵘, 等. 南海珠江口盆地文昌A凹陷低孔低渗油气层测井识别方法及应用 [J]. 海洋地质前沿, 2012, 28(6): 46-50.

[5] 边会媛, 潘保芝. 利用横波数据进行低孔低渗储层气层识别与储层参数定量评价 [J]. 吉林大学学报: 自然科学版, 2010, 40(增刊): 106-109.

[6] Biot M A. General Theory of Three-dimensional Consolidation [J]. Journal of applied physics, 1941, 12(2): 155-164.

[7] Gassmann F. Elastic Waves Through a Packing of Spheres [J]. 1951, 16(14): 673-685.

[8] Mavko G, Mukerji T, Dvorkin J. The Rock Physics Handbook: Tools for Seismic Analysis of Porous Media [M]. New York: Cambridge University Press, 2009.

[9] Murphy W, Reischer A, Hsu K. Modulus Decomposition of Compressional and Shear Velocities in Sand Bodies [J]. Geophysics, 1993, 58(2): 227-239.

[10] Russell B H, Hedlin K, Hilterman F J, et al. Fluid Property Discrimination with AVO: A Biot-Gassmann Perspective [J]. Geophysics, 2003, 68(1): 29-39.