某水电站开挖岩质边坡稳定分析及加固措施优化

柏俊磊，王瑞红，王乐华，汤开宇

(1.中国电建集团 西北勘测设计研究院有限公司，西安 710065；2.三峡大学 土木与建筑学院，湖北 宜昌 443002)

某水电站开挖岩质边坡稳定分析及加固措施优化

柏俊磊1，王瑞红2，王乐华2，汤开宇2

(1.中国电建集团 西北勘测设计研究院有限公司，西安 710065；2.三峡大学 土木与建筑学院，湖北 宜昌 443002)

某水电站泄洪洞进水口边坡为典型的岩质高陡开挖边坡，其稳定性对水电站的安全施工及运行影响重大。为此，建立了泄洪洞所在开挖高边坡的三维有限元模型，并运用有限差分软件进行稳定性分析计算；综合考虑边坡在天然、开挖、卸荷、暴雨蓄水、地震工况下的应力、应变的大小及分布状况，同时结合典型剖面边坡二维极限平衡计算，计算结果中的安全系数大小，综合分析判断泄洪洞进口边坡的稳定性状况；最后结合稳定性分析结果对边坡的加固措施进行了优化分析。成果为工程施工提供参考依据。

边坡；稳定性；有限元；极限平衡；锚固；优化

1 研究背景

在水电站的开发建设中特别是在复杂地质环境下进行水电站建设，往往伴随有高陡边坡的稳定性问题。边坡的稳定与否不仅关系到水电站施工期的安全更重要的是关系到水电站运行期的安全。因此，对边坡进行稳定性分析在水电站的开发建设中是必不可少的，也是岩土工程中一个十分重要的问题。

常用的边坡稳定性分析方法包括刚体极限平衡法和有限元法[1-2]。刚体极限平衡法通过分析岩体滑块在破坏那一刻的平衡来求得滑块的滑动安全系数，判断边坡是否稳定。该方法概念清晰、计算简单，但不能考虑结构的变形效应，而且假定滑动面同时达到极限破坏状态，不能反映滑动面的真实状态; 有限元方法能给出边坡中的应力和位移场，能反映边坡岩体的应力-应变关系，考虑实际边坡体的复杂边界条件，因而是一种较好的研究边坡稳定性的方法[3-4]。本文主要采用三维有限差分法对泄洪洞进口边坡进行稳定性计算，同时结合典型剖面边坡的二维极限平衡计算结果，综合分析判断泄洪洞进口边坡岩体的稳定性，最后在原有初始锚固方式的基础上，根据稳定性计算结果利用二维有限元分析的方法对开挖边坡的锚固措施再进行优化设计。

2 实例分析

2.1 工程概况

某水电站以发电为主，泄洪洞进口位于右岸坝线上游400～450 m处的一小山梁下部，斜坡上部高程2 480 m，岸坡高差达400 m，岸坡整体坡度50°左右，进水口上游侧分布有一条切割深度<10 m的冲沟。进口部位除两侧较低洼处分布有少量崩坡碎石土外，绝大部分地段基岩裸露。岩性为T3z2(7)、T3z2(8)岩组薄—中厚层状变质细砂岩夹碳质千枚岩，岩层产状NW330°～340°SW∠40°～60°。

2.2 计算参数

根据地质资料以及相关试验结果选取合理的岩体物理力学参数，设计计算参数值如表1所示。

3 三维有限差分分析

3.1 三维模型

三维模型选取右岸泄洪洞开挖边坡为研究对象，模型y向645 m，x向632 m，模型最低点高程1 700 m，最高点高程为2 560 m；其中x为垂直于泄洪洞方向即顺河流方向，以向下游为正；y为平行于泄洪洞方向即沿坡向，以顺坡向为正；z为高程方向，以向上为正。

三维模型主要采用四面体划分网格，共有56 725个节点和268 235个单元，模型网格图见图1所示。

表1 岩体的物理力学参数Table 1 Physical and mechanical parameters of rock mass

图1 三维模型网格Fig.1 Meshes of 3-D model

3.2 计算工况

采用Flac3D有限差分计算软件计算考虑以下5种工况：①自然工况，即边坡开挖前原始工况；②开挖工况，即不考虑卸荷作用的边坡开挖工况；③卸荷工况，考虑开挖卸荷作用的动态变化过程；④暴雨蓄水工况，此工况主要模拟正常蓄水位运行时，分析边坡在蓄水位暴雨作用下的稳定情况，在考虑蓄水的情况下，计算时对蓄水位线以下岩层的抗剪强度力学参数值取；⑤蓄水地震工况，此工况主要模拟正常蓄水位且地震作用下边坡的稳定情况，进口边坡地震设防标准按50 a超越概率10%的地震动参数进行设计，对应的基岩水平峰值加速度分别为0.097g。

图2 典型剖面示意图Fig.2 Typical profile

3.3 计算结果分析

根据各个工况的计算要求，充分考虑典型剖面上的应力、应变大小分布情况，同时根据需要选取如图2中所示的垂直于边坡开挖面的纵剖面以及侧坡的6—6剖面为典型剖面，基于三维有限差分的计算结果分析边坡稳定性。

三维有限差分计算成果表明：边坡模型位移以及应力在开挖工况下与自然工况相比有所增大，最大向坡外位移达到0.41 cm；而在卸荷工况下，相比于开挖工况，最大向坡外位移大幅增加达到1.76 cm；暴雨蓄水工况下，边坡模型最大位移以及拉应力相对于开挖卸荷工况有明显增大，最大向坡外位移达到2.86 cm，最大拉应力增加到0.782 MPa；在地震作用这种偶然工况下，边坡模型最大位移以及拉应力相对于其它工况进一步明显增大，最大向坡外位移达到3.43 cm，最大拉应力增加到1.581 MPa。开挖工况、卸荷工况、蓄水暴雨3种工况下y向最大位移的发生位置均在2 230 m高程附近，可以看出在暴雨蓄水和地震作用下坡体稳定性受到的影响较大，但受影响区域主要集中在2 230 m高程上下，即主要集中在开挖面的中下部位置，因此,在后续施工中应加强对该区域岩体进行加固。

4 二维极限平衡分析

4.1 计算原理

边坡沿着某一滑裂面滑动的安全系数F是表征边坡抗滑稳定程度的指标，是抗滑力与滑动力之比，严格说是假定岩土体沿特定滑面达到极限平衡状态时，抗剪强度参数应缩减的倍数，即抗剪强度指标降低为σ3max和tanφ′/F，即

上述将强度指标的储备作为安全系数定义的方法是经过多年的实践被工程界广泛承认的一种方法[5-6]。

图3 边坡稳定的条分法Fig.3 Schematic diagram of strip method for slope stability analysis

二维极限平衡主要是相应的滑动块体满足相应的静力平衡条件，将滑动体分成若干条(如图3所示)，每个条和整个滑动体都要满足力和力矩平衡条件。在静力平衡方程组中，未知数的数目超过方程式的数目，解决这一静不定问题的办法是对多余未知数作假定，使剩下的未知数和方程数目相等，从而解出安全系数的值。

4.2 计算结果分析

根据有限差分的计算结果，发现泄洪洞进口侧坡(6—6剖面)的稳定性更差，基于此，通过二维刚体极限平衡法，主要对泄洪洞进口侧坡(6—6剖面)进行稳定计算，分别计算天然工况、施工期的开挖工况、卸荷工况以及运行期的加固+蓄水暴雨、加固+蓄水地震等复杂工况，其中加固方式按照初始设定的初步加固方案设定。

由表2可以看出，典型剖面(6—6)在5种工况下安全系数均满足水电水利工程边坡设计安全系数[7]的要求，且在天然工况、施工期的开挖工况、卸荷工况下的安全系数均较大，在运行期的2种工况下安全系数基本满足要求，说明开挖卸荷加固后变形体强度能满足工程设计要求，在持久工况下边坡稳定状况较好，而在短暂工况以及偶然工况下边坡的安全系数也能基本满足要求，这与利用有限差分法计算得出的结论趋于相同。为了电站边坡的长期安全稳定运行，仍然要对加固措施进行优化设计。

表2 典型剖面边坡极限平衡计算结果Table 2 Result of limit equilibrium calculation fortypical profile

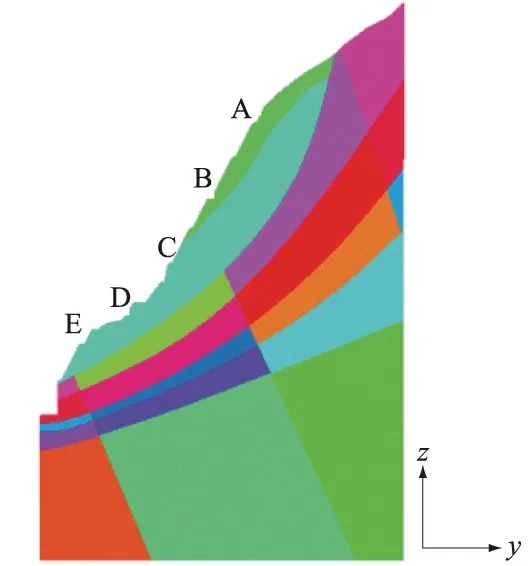
图4 材料分区Fig.4 Material zoning

5 锚固措施优化分析

锚固方式优化主要以Adina有限元计算程序为平台，进行二维有限元模型的建立﹑计算以及锚固方式的模拟，二维材料分区图如图4所示。在Adina有限元程序中，可以通过Truss单元来模拟锚索和锚杆。在模拟锚索时，需要输入锚索截面积和初始应变2个参数。锚杆和锚筋桩则只有截面积1个参数。按ASTM A416—97的规定：锚索预应力为1 000 kN时，锚索截面积为0.000 98 m2，初始应变为0.004 859。Φ28锚筋桩和Φ28锚杆的横截面积为0.000 616 m2，Φ25锚杆的横截面积为0.000 491 m2。

同时选取5个代表性点作为关键点(如图4中的A，B，C，D，E所示)，关键点高程见表3。分析关键点在开挖锚固过程中的位移和应力变化趋势，见图5所示。

表3 关键点对应高程表Table 3 Elevations of key points

图5 关键点的y向位移和第一主应力变化Fig.5 Variations of displacement in y direction and first principal stress of key points

为了分析不同锚固方案对边坡稳定性的影响，拟采用4种方案(其中方案4为建议加固方式)进行分析比较。方案1： 在高程2 226，2 250，2 275，2 295 m各布置2排锚索；方案2：在高程2 226，2 250，2 275，2 295，2 330 m各布置2排锚索；方案3：在高程2 226，2 275，2 295，2 330 m附近各布置2排锚索，2 250 m附近各布置3排锚索；方案4：在高程2 226，2 275，2 295，2 330 m附近各布置2排锚索，2 250 m附近各布置4排锚索。

这4种方案中预应力锚索均采用间排距4 m，锚固角15°，吨位1 000 kN的布置参数。以往的研究成果表明，采用长度一致的锚索加固边坡将会影响坡体整体稳定性，因此，根据该坡体的实际情况采用长度为20 m和25 m的预应力锚索交替布置。4种方案的最大拉应力、向坡外最大位移的计算结果如表4所示。

表4 二维有限元计算成果Table 4 Result of two-dimensional finite element calculation

5.1 位移分析

从表4中可以看出：开挖边坡加固前与加固后相比，以及随着锚索数量的增加，边坡向坡外的最大相对位移有所减少；从关键点曲线来看(图5)：关键点在开挖的过程中水平向位移大都指向坡外，且随着锚索数量的增加向坡外位移有所减小，边坡y向最大相对位移变化不是很明显；随着锚索数量的增加z负向位移基本保持不变。

5.2 应力分析

从表4中可以看出：开挖边坡加固前与加固后相比，以及随着锚索数量的增加，第一主应力，第三主应力中的拉应力在逐渐减小，第一主应力，第三主应力中的压应力变化不大；变化幅度均不明显；从关键点曲线来看(图5)：主要集中在关键点A，C，D，E位置处的变化较为明显，这是由于锚索数量的变化主要集中于关键点C，D位置附近，可以看出边坡加固与否，以及随着锚索数量的变化，对应力的影响较之位移要明显，且随着锚索数量的增加，拉应力均逐渐减小。

5.3 塑性区分析

塑性区分布如图6所示。

图6 5种情况下塑性区分布Fig.6 Distribution of plastic zone in five cases

加固后与加固前相比，塑性区的范围有了较为明显的减少，说明加固措施对开挖边坡塑性区范围影响较为明显；锚索数量的增加对开挖边坡塑性区影响不够明显。

综上所述，可以发现采用方案1的实际锚固效果和初始建议加固方案的效果基本上是一样的，实际施工中可以根据实际情况适当减少锚索数量。

5.4 不同锚固方式对比分析

根据初始设计，选取3种锚固方式对比分析：①仅施加锚索；②在加锚索的基础上增加Φ28锁口锚杆和Φ28锚筋桩；③在之前加固措施的基础上再增加Φ25系统锚杆。3种不同锚固方式下向坡外位移等值线图和塑性区分布如图7所示。

图7 3种不同锚固方式下塑性区分布Fig.7 Plastic zone distribution in the presence of three different ways of anchoring

塑性区比较发现，在加锚索的基础上又加Φ28锁口锚杆和Φ28锚筋桩对开挖坡体表面和内部塑性区范围分布均有一定的影响，且有减少内部塑性区分布范围的作用，在之前加固措施的基础上再加Φ25系统锚杆可以减少部分开挖坡体表面塑性区的分布范围，但效果均不是太明显。

6 结 论

文章结合三维有限差分方法、二维极限平衡法以及二维有限元方法对该水电站泄洪洞进口岩质开挖边坡进行了稳定性分析，并结合稳定性分析的结果对锚固措施进行了优化设计，得到以下结论：

(1) 三维有限差分方法、二维极限平衡法的分析结果可以说明该岩质开挖边坡在施工期以及持久工况下的稳定状况良好，不会出现整体边坡失稳的状况，而在暴雨、地震等短暂或偶然工况下，边坡开挖岩体位移以及拉应力明显增大，稳定性安全系数也明显变小，但基本能满足相关要求，说明现有的加固措施可以基本满足边坡稳定性的要求，但应注意开挖边坡中下部岩体的变形情况，施工及运行期需要加强监测。

(2) 通过对开挖工况和卸荷工况下的边坡位移、应力以及极限平衡分析发现，卸荷工况下的位移、应力要明显大于开挖工况，且安全系数后者也比前者有明显的减小，因此，在对岩质开挖边坡的稳定性分析时应充分考虑开挖卸荷引起的岩体劣化作用。

(3) 锚固措施的优化分析结果发现：增加锚索的数量对减少开挖边坡的岩体位移以及塑性区范围的效果并不是特别明显，实际施工中可以根据实际情况适当选择锚索数量，在原有设计的基础上可以适当减少锚索数量；而3种锚固方式对比分析结果发现，增加锁口锚杆、锚筋桩以及系统锚杆的方式虽然可以减少部分开挖坡体表面塑性区的分布范围，但是效果不太明显，因此，在施工中应根据实际情况灵活选择是否需要增加这些锚固措施。

[1] 许建聪，尚岳全，陈侃福，等. 顺层滑坡弹塑性接触有限元稳定性分析[J].岩石力学与工程学报，2005,24(13)：2231-2236. (XU Jian-cong, SHANG Yue-quan, CHEN Kan-fu,etal. Elastoplastic Contact FEM Analysis of Bedding Landslide Stability[J]. Chinese Journal of Rock Mechanics and Engineering, 2005,24(13)：2231-2236.(in Chinese))

[2] 刘立平，姜德义，郑硕才，等. 边坡稳定性分析方法的最新进展[J].重庆大学学报：自然科学版，2000，23(3)：115-118. (LIU Li-ping，JIANG De-yi，ZHENG Shuo-cai，etal. Recent Progress of the Slope Stability Analysis Methods[J]. Journal of Chongqing University: Natural Science, 2000, 23(3): 115-118.(in Chinese))

[3] 李建林，王乐华，刘 杰,等.岩石边坡工程[M].北京：中国水利水电出版社，2006.(LI Jian-lin, WANG Le-hua, LIU Jie,etal. Rock Slope Engineering[M]. Beijing: China Water Power Press，2006.(in Chinese))

[4] 佴 磊,徐 燕,代树林,等.边坡工程[M].北京：科学出版社，2010.(ER Lei，XU Yan，DAI Shu-lin，etal. Slope Engineering [M]. Beijing : Science Press, 2010 . (in Chinese))

[5] 郑颖人，赵尚毅，张鲁渝. 用有限元强度折减法进行边坡稳定分析[J]. 中国工程科学，2002，4(10)：57-61. (ZHENG Ying-ren，ZHAO Shang-yi，ZHANG Lu-yu. Slope Stability Analysis by Strength Reduction FEM[J]. Engineering Science，2002，4(10)：57-61.(in Chinese))

[6] 陈祖煜. 土质边坡稳定分析—原理·方法·程序[M]. 北京：中国水利水电出版社，2003. (CHEN Zu-yu. Stability Analysis of Soil Slope: Principles, Methods, and Program[M]. Beijing：China Water Power Press, 2003. (in Chinese))

[7] SL386—2007, 水利水电工程边坡设计规范[S]. 北京：中国水利水电出版社，2007. (SL386—2007, Specifications for Slope Design in Water Resources and Hydropower Engineering[S]. Beijing：China Water Power Press，2007. (in Chinese))

(编辑：王 慰)

Stability Analysis and Reinforcement Optimizationfor an Excavated Rock Slope

BAI Jun-lei1, WANG Rui-hong2, WANG Le-hua2, TANG Kai-yu2

(1.Power China Xibei Engineering Corporation Limited, Xi’an 710065, China;2.College of Civil Engineering and Architecture, China Three Gorges University, Yichang 443002, China)

The intake slope of the spillway tunnel of a hydropower station is a typical high steep rock excavation slope. Its stability has a significant impact on the safe construction and operation of the station. In this research, 3-D finite element model is established for the slope and stability analysis is conducted by using finite difference software. The stress, strain, and the size and distribution of plastic zone in natural condition, excavation and deloading condition, rainstorm and seismic conditions are comprehensively considered in the model. Furthermore, according to the safety factor from two-dimensional limit equilibrium calculation for typical profile, the slope stability is determined. Moreover, the reinforcement measures are optimized based on the stability calculation results.

slope; stability; finite element; limit equilibrium; anchorage; optimization

2013-09-30；

2014-01-08

国家自然科学基金项目(51109120，50909052，51279091)

柏俊磊(1988-)，男，湖北十堰人，助理工程师，主要从事岩石边坡工程设计与理论方面的研究，(电话)18392151889(电子信箱)bjl8810@126.com。

10.3969/j.issn.1001-5485.2015.02.020

TU47

A

1001-5485(2015)02-0098-05

2015,32(02):98-102